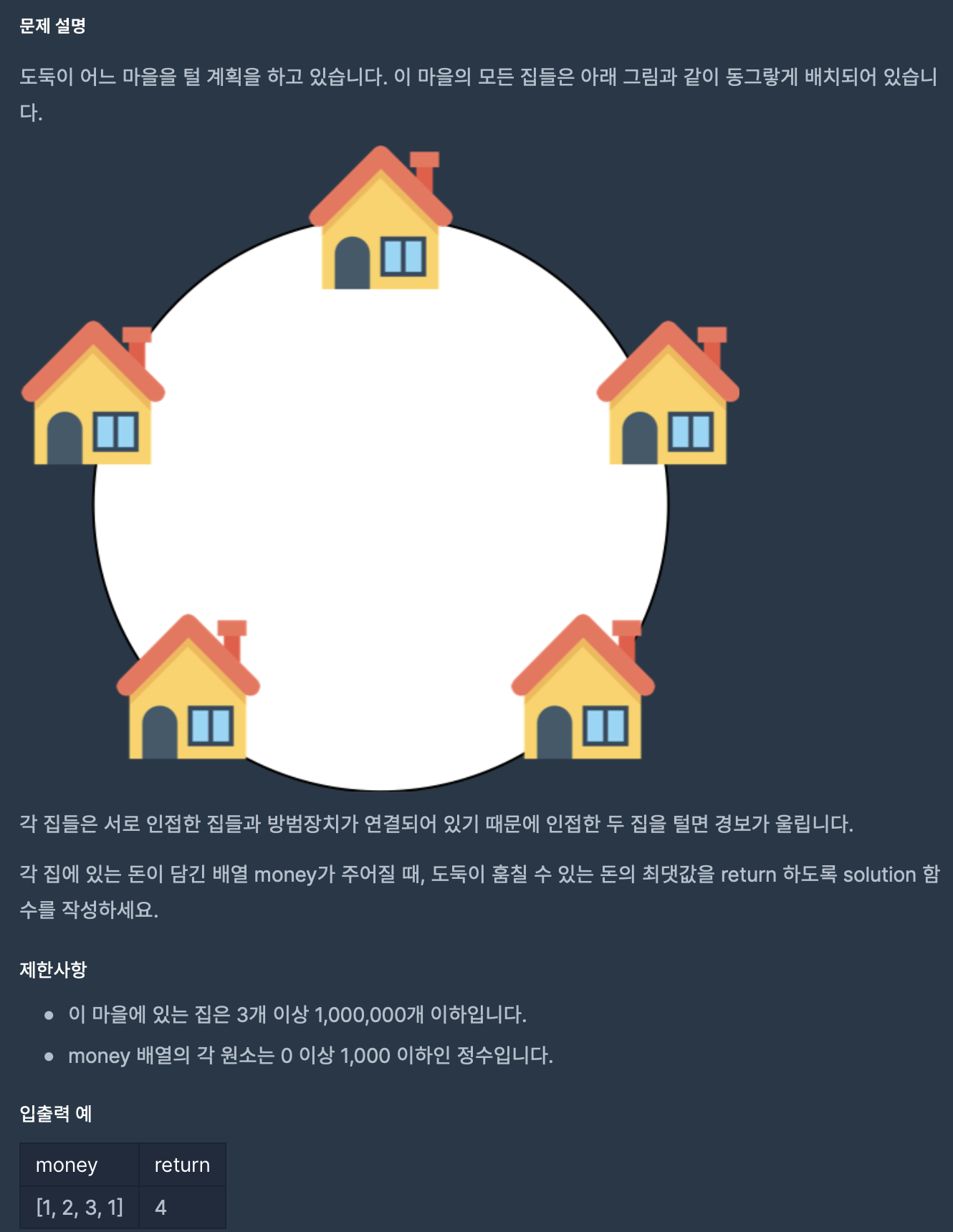
문제 설명
예제 설명
인접한 두 집을 털지 않는 방법은 0번, 2번 집을 터는 경우이다.
구현 아이디어 1
문제 상황을 표로 그려서 생각해보면 아래와 같다.
| index | n번 집까지 고려했을 때 최댓값 |
|---|---|
| 0 | money[0] |
| 1 | max(money[0], money[1]) |
| 2 | max(dp[0] + money[2], money[2]) |
| 3 | max(dp[1] + money[3], money[3]) |
| i | max(dp[i-2] + money[i], money[i-1]) |
전체 코드 - 틀렸습니다
def solution(money):
dp = [0 for _ in range(len(money))]
dp[0] = money[0]
dp[1] = max(money[0], money[1])
for i in range(2, len(money)):
dp[i] = max(dp[i-2]+money[i], dp[i-1])
return dp[-1]
반례
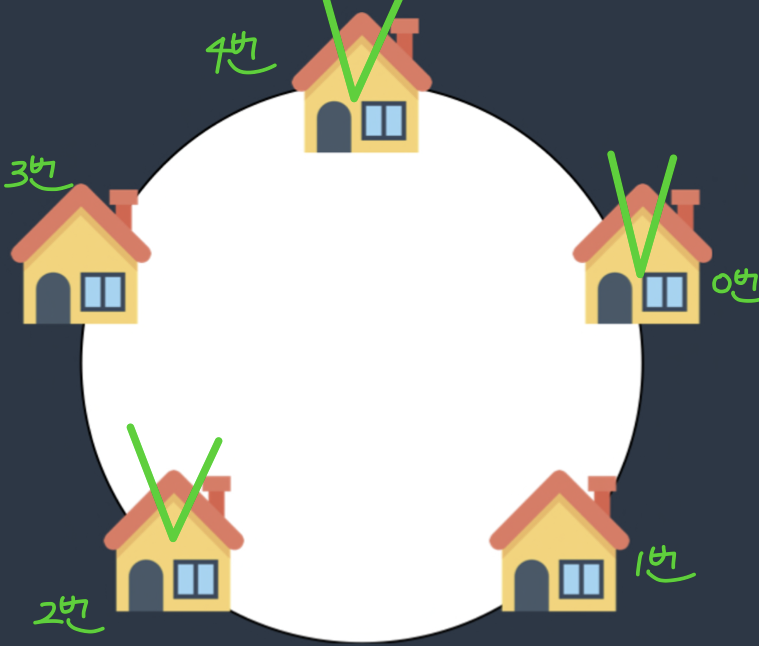
위와 같은 상황에서
dp[4] = max(dp[2] + money[4], money[3])이다.
이 때, dp[2] + money[4] > money[3]이고, dp[2] = 0번 집과 2번 집을 털었을 경우라고 생각하면 결과적으로 0번, 2번, 4번 집을 터는 것이 내가 세운 점화식의 해이다.
그러나 💥마을이 동그랗게 배치되었기 때문에, 0번 집과 4번 집은 인접한 집이므로 동시에 털 수 없다💥
구현 아이디어 2
우리는 첫 번째 집과 마지막 집을 동시에 털지 않도록 주의해야 한다.
그렇기 위해서
- 첫 번째 집을 털었으면, 마지막 집을 털지 않아야 하고
- 마지막 집을 털었으면, 첫 번째 집을 털지 않아야 한다.
이를 구현하기 위해 첫 번째 집을 털 경우와 마지막 집을 털 경우 두 가지로 나누어 각각 최댓값을 구해 더 큰 값을 선택하는 방법을 생각했다.
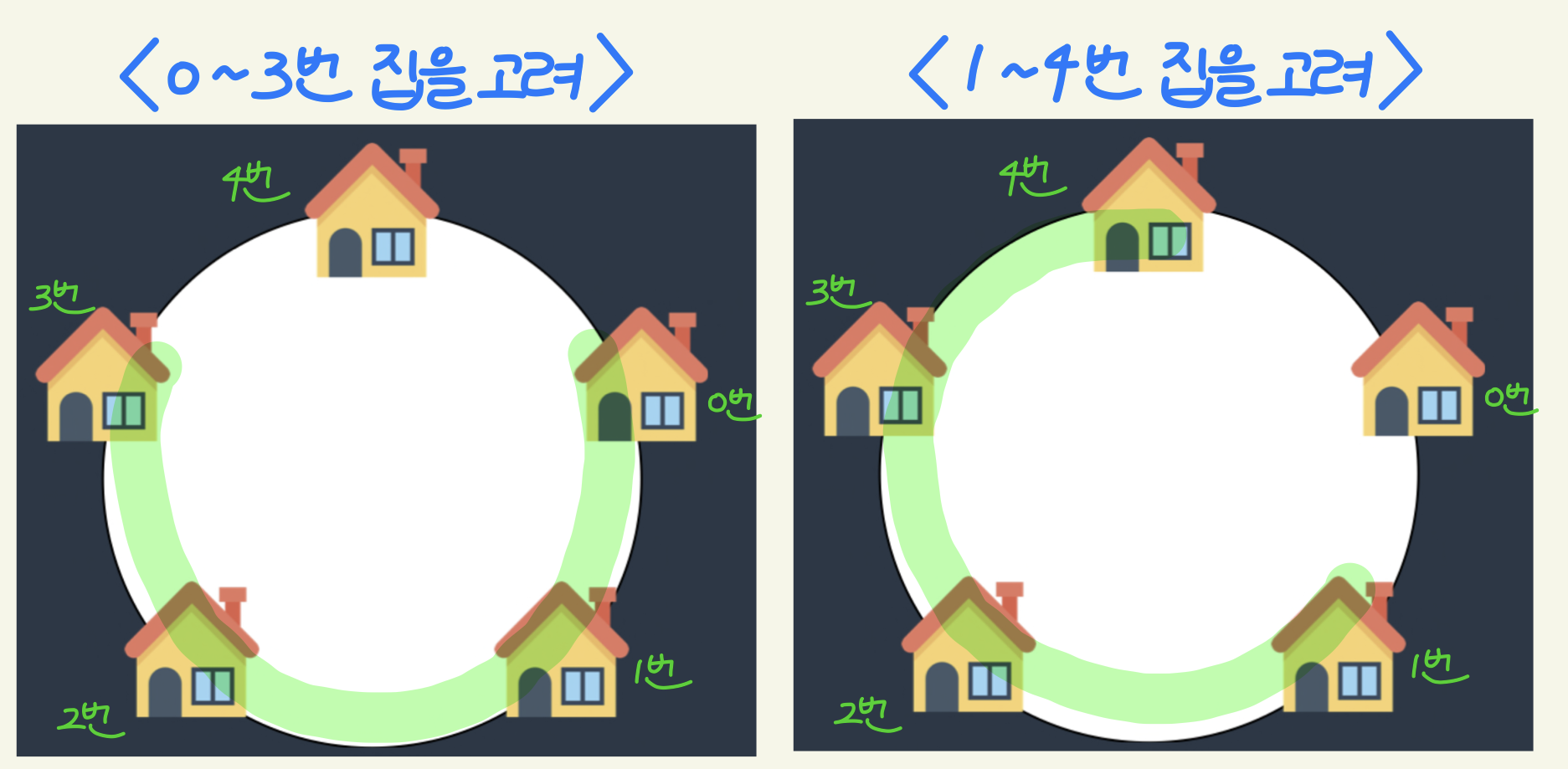
그림과 같이 5개의 집이 있다고 가정하면,
- 0번 ~ 3번 집만 고려하는 경우
- 1번 ~ 4번 집만 고려하는 경우
로 나눈다. 이렇게 되면 0번 집과 4번 집을 동시에 터는 경우를 없앨 수 있다.
전체 코드 - 정답입니다
def solution(money):
zero = [0 for _ in range(len(money)-1)] # 0번 ~ (n-1)번 집을 고려하는 경우
one = [0 for _ in range(len(money)-1)] # 1번 ~ n번 집을 고려하는 경우
zero[0] = money[0]
zero[1] = max(money[0], money[1])
one[0] = money[1]
one[1] = max(money[1], money[2])
for i in range(2, len(zero)):
zero[i] = max(zero[i-2]+money[i], zero[i-1])
for i in range(2, len(one)):
one[i] = max(one[i-2]+money[i+1], one[i-1]) # index를 주의하여 식을 세우자
return max(zero[-1], one[-1])