프로그래머스 - 디스크 컨트롤러 풀러 가기

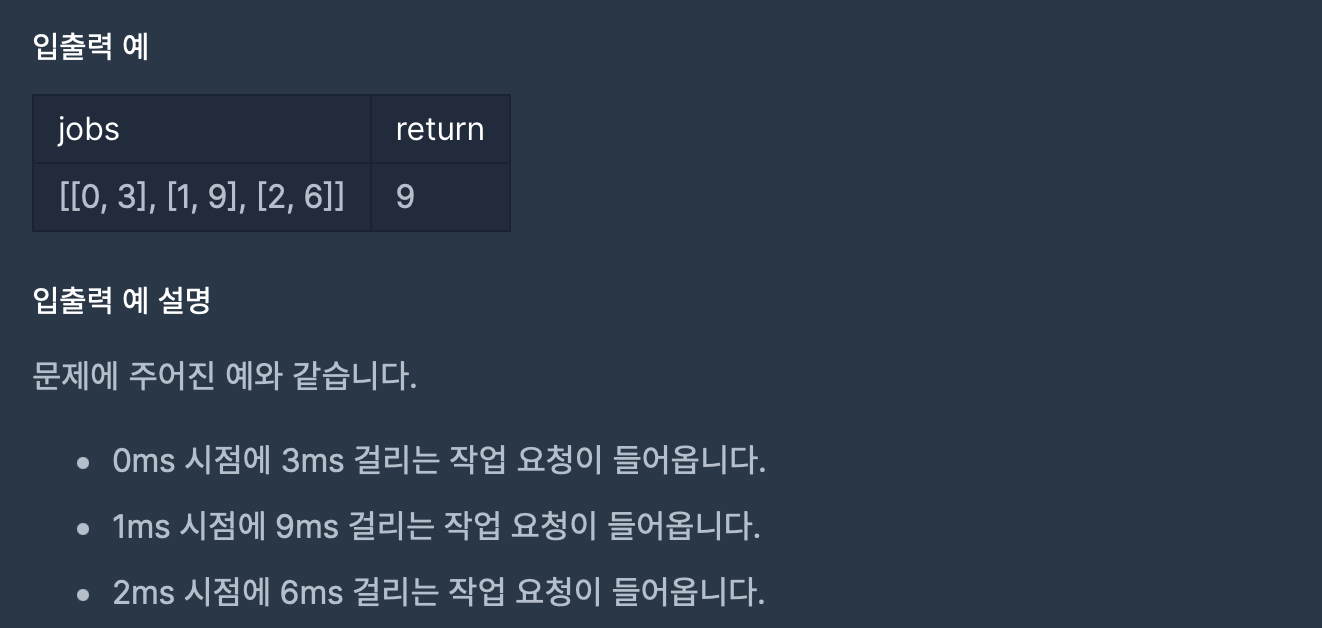
문제 설명

구현 아이디어

특정 규칙에 따라 작업의 우선 순위를 구하고, 순서에 따라 작업을 수행해야 함 → 힙을 사용하자

그럼 작업들은 어떤 우선 순위로 구할까?🤔

1. 먼저 들어온 순서?
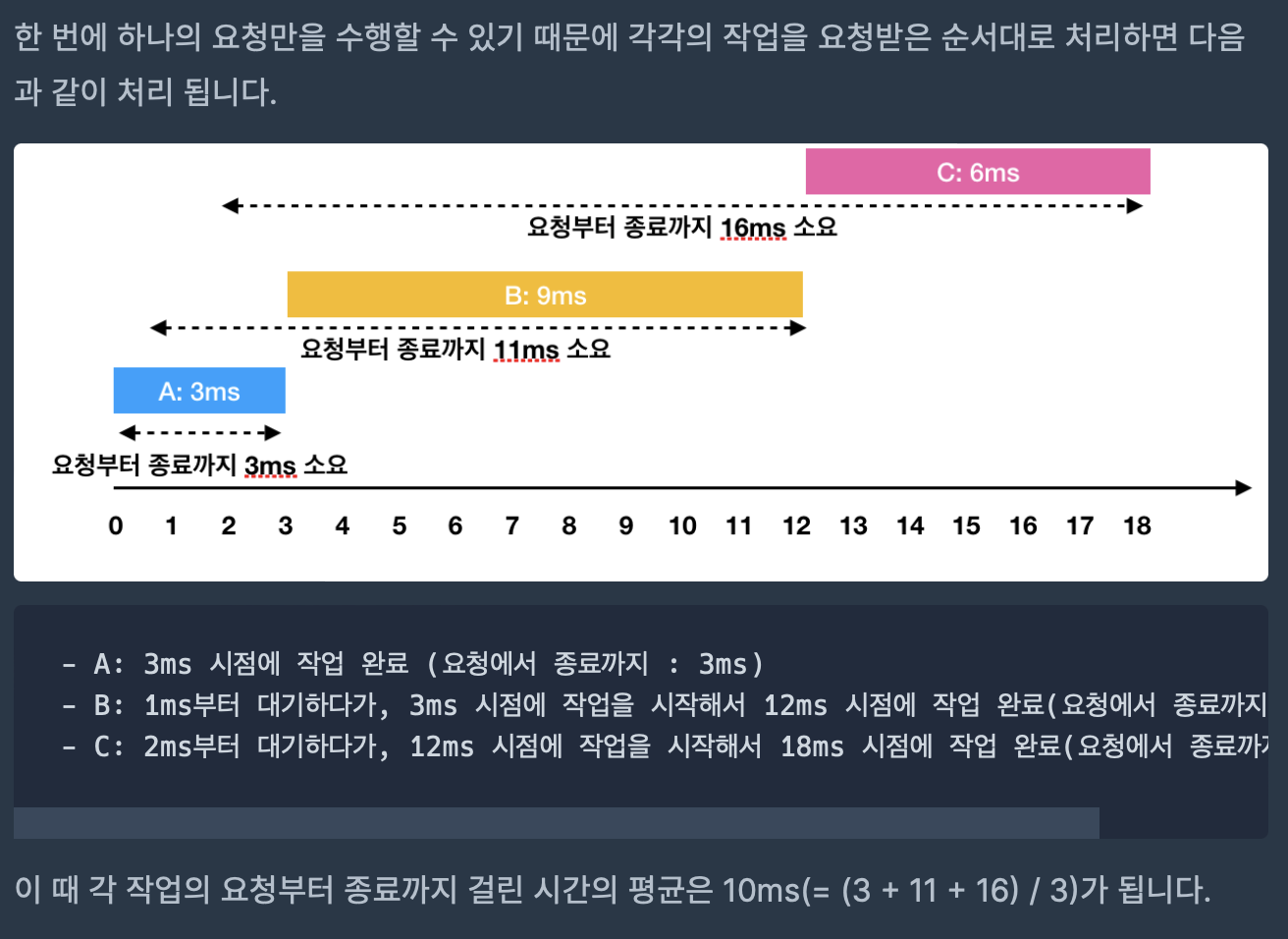
   → 위 예제를 통해 들어온 순서대로 처리하면 최소가 아님을 알 수 있다.

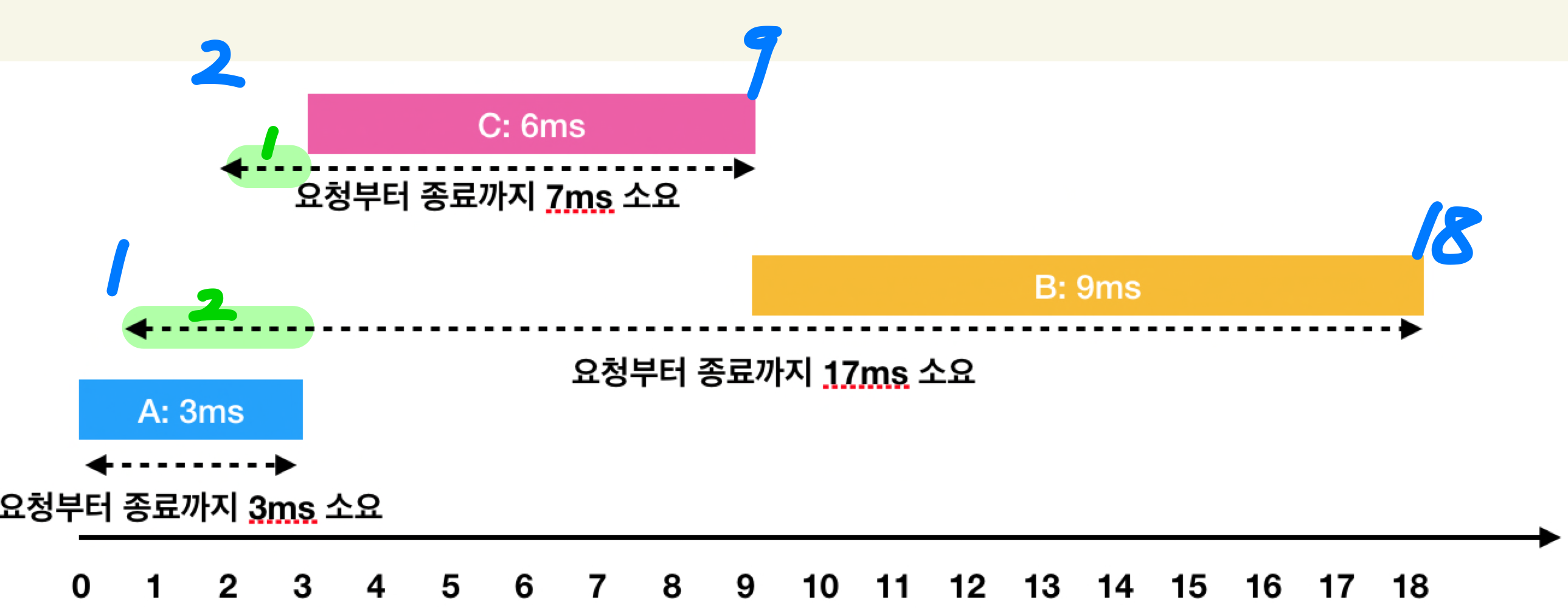
2. 위 예제에서 보면 A, B, C는 (앞 요청이 끝나는 시간 - 요청이 들어온 시점) + 작업 수행 시간이 짧은 순서임을 알 수 있다.

하지만 ... 이 방법으로 하면 앞 요청이 끝나는 시간이 계속 달라지기 때문에 힙에 담아야 할 값이 동적으로 변한다.
결국 코드를 작성할 아이디어가 도저히 떠오르지 않아 ... 다른 사람의 코드를 참고했다 ... 🫠

풀이 과정

현재 시점에서 처리할 수 있는 작업을 힙에 넣고 처리하자

• 작업의 소요 시간을 기준으로 힙에 원소를 삽입
• 현재 시점에서 처리할 수 있는 작업을 판별하는 기준
  • 바로 이전 작업의 시작 시점 ≤ 작업 요청 시점 ≤ 현재 시점

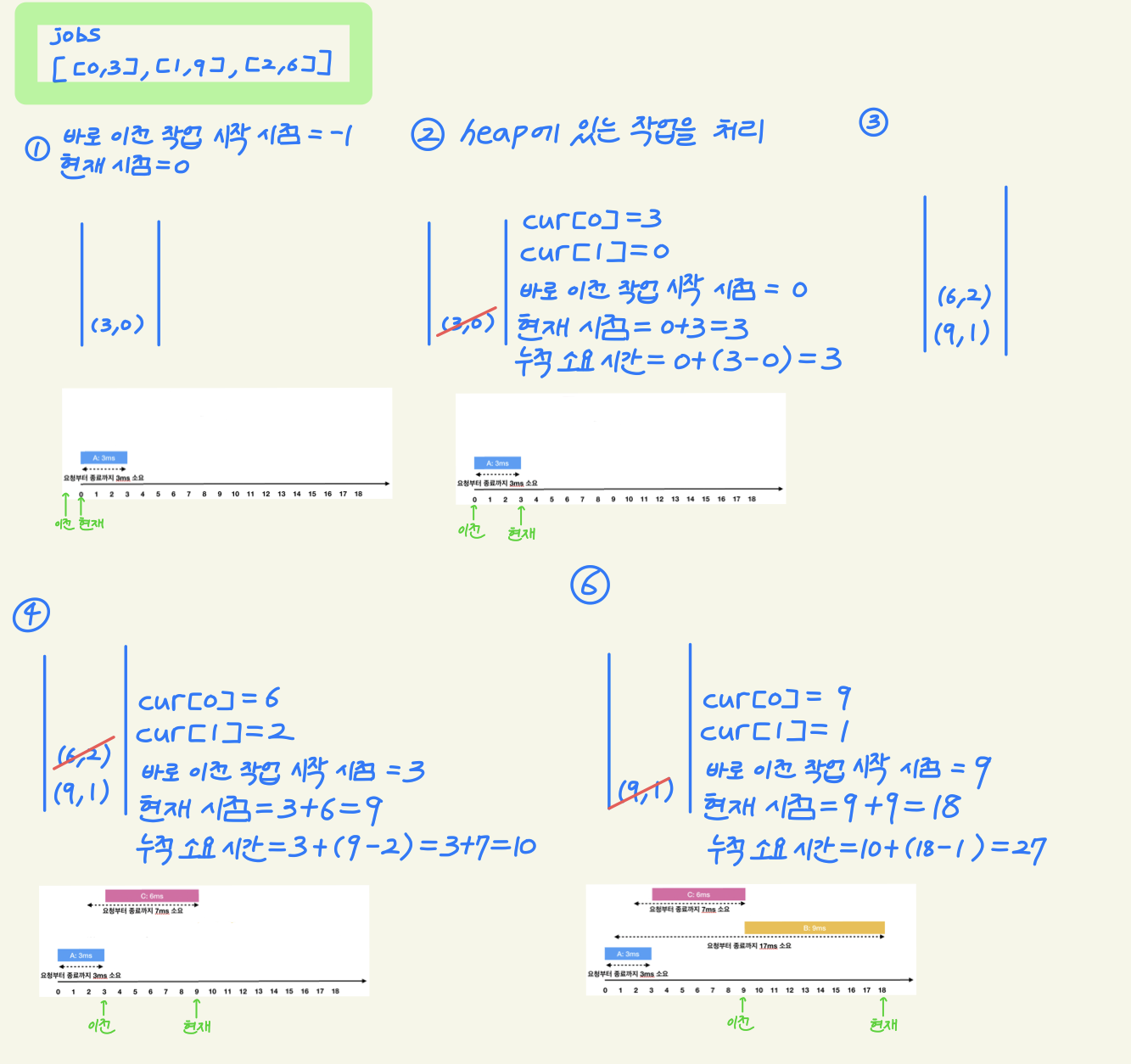
1️⃣ 처음에는 이전 작업 시작 시점이 없기 때문에 -1로 하고, 현재 시점은 0으로 한다.
작업 요청 시점이 -1과 0 사이인 작업은 [0, 3]만 있기 때문에 이것을 힙에 삽입한다.

2️⃣ 힙에 있는 작업들을 처리한다.
바로 이전 작업 시작 시점을 현재 작업 시작 시점으로 갱신하고, 현재 시점을 갱신한다.
누적 소요 시간도 계산한다.

3️⃣ 이전 작업 시작 시점은 0, 현재 시점은 3이 되었다.
작업 요청 시점이 0과 3 사이에 있는 [1, 9]와 [2, 6]을 힙에 삽입한다.

4️⃣ 힙에 있는 작업들을 처리한다.
작업의 소요 시간을 기준으로 우선 순위가 계산되므로 [2, 6]이 먼저 처리되고 그 다음 [1, 9]가 처리된다.

코드

# 1. 힙 자료구조를 사용하기 위해 라이브러리를 불러온다
import heapq

def solution(jobs):
	# 1. 사용할 변수 초기화
    
	# answer - 누적 소요 시간 / now - 현재 시점 / i - 수행한 작업의 갯수
    answer, now, i = 0, 0, 0
    # start - 이전 작업 시작 시점
    start = -1
    heap = [] # 힙으로 사용할 리스트
    
    # 2. 작업들을 처리
    
    # 모든 원소에 대해 진행
    while i < len(jobs):
        for j in jobs:
        	# 2-1. 현재 시점에 처리할 작업이 있다면 힙에 원소를 삽입한다.
            # 바로 이전 작업의 시작 시점 ≤ 작업 요청 시점 ≤ 현재 시점
            # 이 때 소요 시간이 첫 번째 원소가 되도록 삽입한다.
            if start<j[0]<=now:
                heapq.heappush(heap, [j[1], j[0]]) # 소요 시간, 요청 시점 순으로 담음
        # 2-2. 작업들을 처리
        if len(heap) > 0:
            cur = heapq.heappop(heap) # cur[0] - 소요 시간, cur[1] - 요청 시점
            start = now # 이전 작업 시작 시점을 현재 시점으로 갱신
            now += cur[0] # 요청을 처리한 후로 현재 시점도 갱신
            answer += (now-cur[1]) # 누적 소요 시간 계산
            i += 1 # 작업을 수행할 때마다 증가
            
        # 2-3. 처리할 작업이 없다면 현재 시점을 갱신
        else:
            now += 1
            
    # 소수점 이하는 버리기 위해 // 연산을 사용           
    return answer//len(jobs)

TMI

우선순위 큐 VS 힙

• 우선순위 큐 - 들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나오는 것 → 추상적인 자료형
• 힙 - 우선순위 큐를 위해 고안된 완전이진트리 형태의 자료구조