[Level 3 / 그래프] 합승 택시 요금 + Swift

문제 링크

코딩테스트 연습 - 합승 택시 요금

플로이드 와샬(Floyd Warshall) 알고리즘

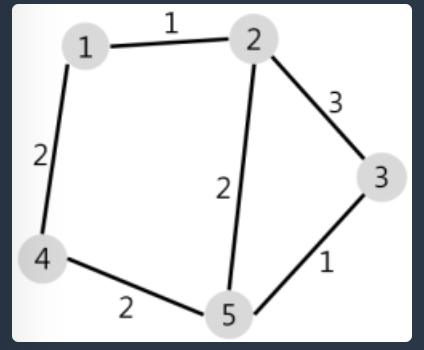
노드 1에서 노드 5까지 가는 경우는 다음과 같다.

1. 1 → 2→ 3 → 5: 비용은 1 + 3 + 1로 총 5이다.
2. 1 → 2 → 5: 비용은 1 + 2로 총 3이다.
3. 1 → 4 → 5: 비용은 2 + 2로 총 4이다.

따라서 1에서 5까지 가는 최소 비용은 3이다. 플로이드 알고리즘은 이런 경우에 유용하다.

문제

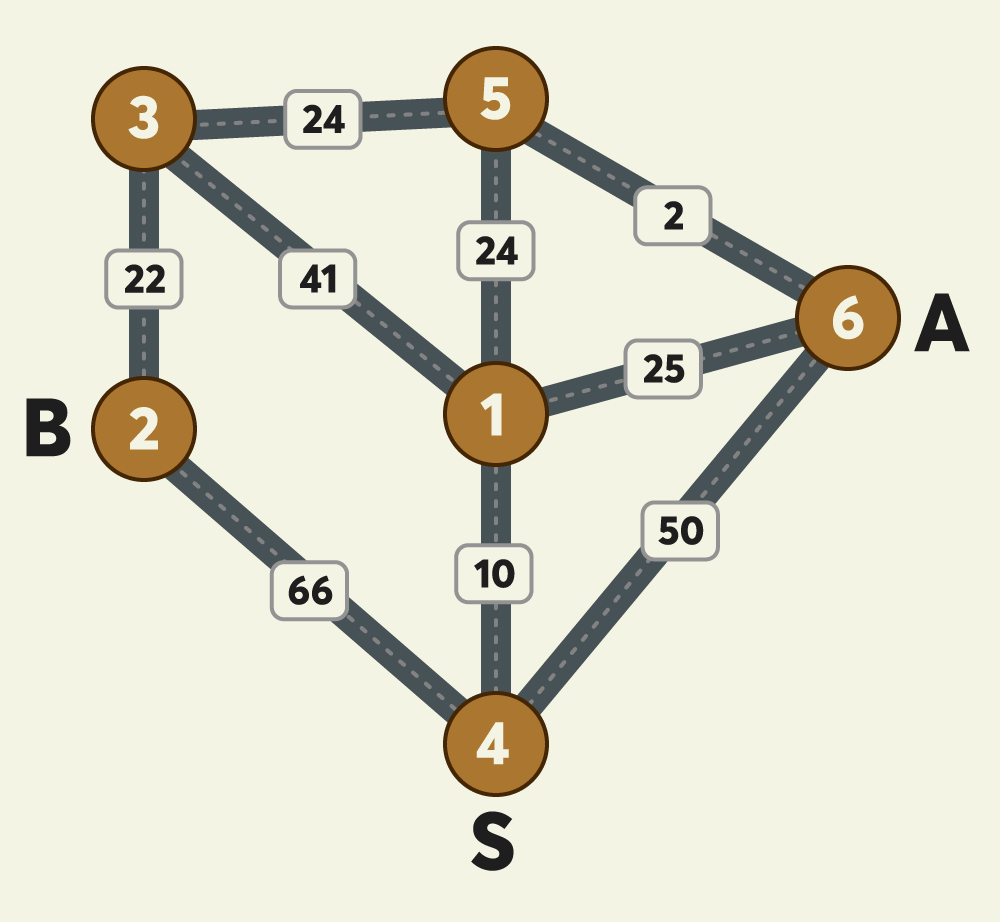
지점의 개수 n, 출발지점을 나타내는 s, A의 도착지점을 나타내는 a, B의 도착지점을 나타내는 b, 지점 사이의 예상 택시요금을 나타내는 fares가 매개변수로 주어집니다. 이때, A, B 두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 가정할 때, 최저 예상 택시요금을 계산해서 return 하도록 solution 함수를 완성해 주세요. 만약, 아예 합승을 하지 않고 각자 이동하는 경우의 예상 택시요금이 더 낮다면, 합승을 하지 않아도 됩니다.

입력

let n = 6
let s = 4
let a = 6
let b = 2
let fares = [[4, 1, 10], [3, 5, 24], [5, 6, 2], [3, 1, 41], [5, 1, 24], [4, 6, 50], [2, 4, 66], [2, 3, 22], [1, 6, 25]]

출력

82

문제 풀이

1. 노드에서 노드까지의 요금을 저장하는 db 이중 배열을 만든다. 요금은 기본값으로 최대 요금(100,000)을 초과하는 값인 999999로 지정한다.

2. 요금배열의 요금을 하나씩 넣는다. 예를 들면 첫번재 요소인 [4, 1, 10]의 경우 노드 4에서 1까지의 요금이 10이므로 db[1][4]와 db[4][1]에 요금 10을 저장한다.

3. 플로이드 와샬 알고리즘의 핵심이다. for문을 3번 돌며, i부터 k까지의 최소 요금을 저장한다.

   예를 들어, i=4, j=1, k=6인 경우를 살펴보자. 위의 그림을 보면 알 수 있듯, 4에서 6까지의 요금은 50이다. 4에서 1까지의 요금인 10과 1에서 6까지의 요금인 25를 합친 요금 35보다 큰 것을 알 수 있다. db에는 4에서 6까지의 요금인 db[4][6]를 둘을 합친 요금인 (db[4][1] + db[1][6])로 갱신한다.

4. s에서 출발해서 중간 지점인 k까지의 요금과, k에서부터 a와 k에서부터 b까지의 요금의 합을 구하며 최솟값을 찾는다. 중간지점인 k가 s값과 일치한다면, 합승하지 않고 각자 이동하는 것으로 보면 된다.

import Foundation

func solution(_ n:Int, _ s:Int, _ a:Int, _ b:Int, _ fares:[[Int]]) -> Int {
    var db: [[Int]] = Array(repeating: Array(repeating: 999999, count: n+1), count: n+1)
    var minFare = 9999999
    
    for fare in fares {
        db[fare[0]][fare[1]] = fare[2]
        db[fare[1]][fare[0]] = fare[2]
    }
    
    for k in 1...n {
        for i in 1...n {
            for j in 1...n {
                if i == j { db[i][j] = 0 }
                if db[i][j] > db[i][k] + db[k][j] {
                    db[i][j] = db[i][k] + db[k][j]
                }
            }
        }
    }
    
    for midpoint in 1...n {
        let fare = db[s][midpoint] + db[midpoint][a] + db[midpoint][b]
        if minFare > fare { minFare = fare }
    }
    
    return minFare
}

let answer = solution(n, s, a, b, fares)
print(answer)