문제
링크텍스트
다이아몬드V | 백준 4149 | Python3 파이썬 풀이
알고리즘
밀러-라빈 소수 판정법을 사용해야 하는 문제이다. 밀러-라빈 소수 판정법 알고리즘에 대해서는 이 블로그 포스트에서 아주 잘 설명해주셨다.
밀러-라빈 소수 판정법에 대해 간략하게 정리해보자면..
밀러-라빈 소수 판정법은 어떤 홀수 이 소수인지 확률적으로 판별해주는 알고리즘이다. 이 판별법은 매우 큰 홀수에 대해 "합성수일 것이다" 혹은 "소수일 것이다" 라고 판별이 가능하다. 즉, 합성수를 소수라고 잘못 판별할 가능성이 있다고 한다.
이 홀수이면, 은 짝수이고, 따라서 임의의 홀수 와 정수 가 존재하여 이다. 만약 이 소수라면, 보다 작은 양의 정수 에 대해 다음 중 하나가 성립하게 된다.
- 중 적어도 하나에 대해
보조 정리
소수 에 대해 이면 이거나 이다.
증명
합동식의 정의에서 은 의 배수이고, 따라서 과 둘 중하나는 의 배수여야 한다.
페르마의 소정리에 의해서 이다. 보조 정리에 의해 이거나, 이다. 후자가 성립하면 2가 성립하므로 증명이 완료된다. 전자가 성립할 경우에는 보조 정리에 의해 이거나 이다. 또 다시 전자가 성립하게 되면 보조 정리를 이용해 까지 진행한다. 끝까지 진행했는데 이라면 1번이 성립하게 된다. 즉, 결국 둘 중 하나는 반드시 성립한다.
역으로 어떤 홀수 이 보다 작은 양의 정수 에 대해 다음을 만족하면 은 반드시 합성수이다.
- 모두에 대해
따라서 적당한 를 선택하고, 위 조건이 성립하면 이 합성수라고 답하고, 성립하지 않는다면 은 probable prime이라고 한다. 합성수를 소수라고 잘못 판별할 확률을 줄이기 위해서는 최대한 많이 의 값을 바꾸어가며 시험해봐야 한다.
아래는 구현하기 위해 사용한 함수 목록이다.
power : 를 반환한다.
def power(x : int, y : int, p : int) -> int:
res = 1
x = x % p
while y > 0:
if y & 1:
res = (res * x) % p
y = y >> 1
x = (x*x) % p
return resgcd : 두 수의 최대공약수를 반환한다.
def gcd(a : int, b : int) -> int:
if a < b:
a, b = b, a
while b != 0:
r = a % b
a = b
b = r
return amiller_rabin : 밀러-라빈 알고리즘을 통해
def miller_rabin(n : int, a : int) -> bool:
r = 0
d = n - 1
while d % 2 == 0:
r += 1
d = d//2
x = power(a, d, n)
if x == 1 or x == n - 1:
return True
for _ in range(r - 1):
x = power(x, 2, n)
if x == n - 1:
return True
return Falseis_prime : 이 소수인지 판별한다.
def is_prime(n : int) -> bool:
alist = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41]
if n == 1:
return False
if n == 2 or n == 3:
return True
if n % 2 == 0:
return False
for a in alist:
if n == a:
return True
if not miller_rabin(n, a):
return False
return TruepollardRho : 폴라드 로 알고리즘을 통해 인수를 반환한다.
def pollardRho(n : int) -> int:
if is_prime(n):
return n
if n == 1:
return 1
if n % 2 == 0:
return 2
x = random.randrange(2, n)
y = x
c = random.randrange(1, n)
d = 1
while d == 1:
x = ((x ** 2 % n) + c + n) % n
y = ((y ** 2 % n) + c + n) % n
y = ((y ** 2 % n) + c + n) % n
d = gcd(abs(x - y), n)
if d == n:
return pollardRho(n)
if is_prime(d):
return d
else:
return pollardRho(d)코드
import sys
import random
input = sys.stdin.readline
sys.setrecursionlimit(10**4)
def power(x : int, y : int, p : int) -> int:
res = 1
x = x % p
while y > 0:
if y & 1:
res = (res * x) % p
y = y >> 1
x = (x*x) % p
return res
def gcd(a : int, b : int) -> int:
if a < b:
a, b = b, a
while b != 0:
r = a % b
a = b
b = r
return a
def miller_rabin(n : int, a : int) -> bool:
r = 0
d = n - 1
while d % 2 == 0:
r += 1
d = d//2
x = power(a, d, n)
if x == 1 or x == n - 1:
return True
for _ in range(r - 1):
x = power(x, 2, n)
if x == n - 1:
return True
return False
def is_prime(n : int) -> bool:
alist = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41]
if n == 1:
return False
if n == 2 or n == 3:
return True
if n % 2 == 0:
return False
for a in alist:
if n == a:
return True
if not miller_rabin(n, a):
return False
return True
def pollardRho(n : int) -> int:
if is_prime(n):
return n
if n == 1:
return 1
if n % 2 == 0:
return 2
x = random.randrange(2, n)
y = x
c = random.randrange(1, n)
d = 1
while d == 1:
x = ((x ** 2 % n) + c + n) % n
y = ((y ** 2 % n) + c + n) % n
y = ((y ** 2 % n) + c + n) % n
d = gcd(abs(x - y), n)
if d == n:
return pollardRho(n)
if is_prime(d):
return d
else:
return pollardRho(d)
N = int(input())
arr = []
while N > 1:
dv = pollardRho(N)
arr.append(dv)
N = N // dv
arr.sort()
for i in arr:
print(i)먼저, 밀러-라빈 소수 판별법과 폴라드-로 알고리즘에 대해 공부하고, 수학식을 코드로 짜보았는데, 난이도가 매우 높았다.
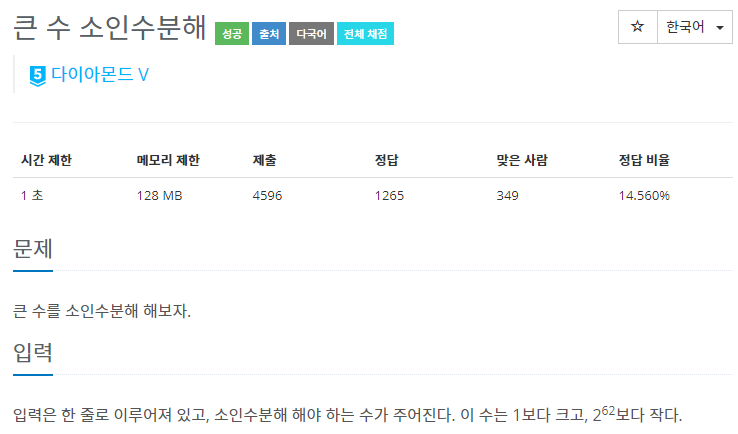
결과