문제 링크

• https://www.acmicpc.net/problem/1647

문제 설명

• 마을에 집들이 있다
• 집들을 연결하는 길들이 있다
• 마을을 두 개로 분할하려 한다
• 그리고 마을 안에서도 유지비를 최소로 하는 길만 남기고 길을 없애려 한다
• 이 때 총 유지비 출력

풀이

• 유지비에 대해 오름차순 정렬
• 두 집이 연결되지 않았을 경우 연결
  • 두 집이 한 집합에 속해 있지 않을 경우 합집합
• 총 N-2개의 길을 선택했을 경우 종료
  • 모든 집을 연결했을 경우 N-1개

Find set & Path compression

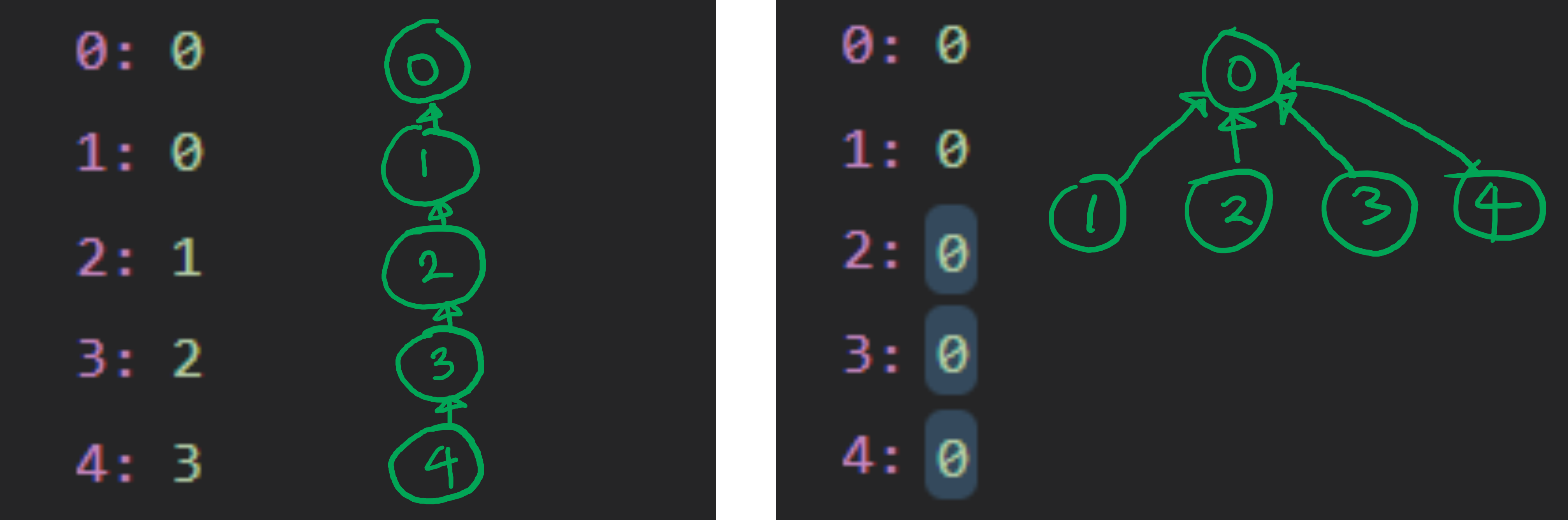
• 원래는 같은 집합인지 판별하기 위한 함수이다
• 부모 노드를 저장하는 리스트를 두고
• 임의의 두 노드의 루트 노드가 같으면 같은 집합
• 그런데 그대로 구현해보니 시간 초과

def find_set(x):
    if x == parent[x]:
        return x
    return find_set_pc(parent[x])

• 해당 코드는 트리의 높이에 비례한다
• 다른 사람들이 올려놓은 코드를 보니 조금 달랐다

def find_set_pc(x):
    if x != parent[x]:
        parent[x] = find_set_pc(parent[x])
    return parent[x]

• 처음에는 왜 이런지 이해를 못했다
• 루트 노드를 구하는데 왜 저장을 하지?
• 그래서 디버깅을 해보니 이유를 알 수 있었다
• 권오흠 교수님이 말씀하신 Path Compression(경로 압축)을 위해서 였다
  • 복잡도가 트리의 높이에 비례하기 때문에 트리의 높이를 줄임
    
• 베스트는 아니지만 재귀가 아닌 반복문으로 구현해보면 이렇다

def find_set_pc(start):
    path = []
    root = start
    while root != parent[root]:
        path.append(root)
        root = parent[root]
    for curr in path:
        parent[curr] = root
    return root

Weighted union

• 일반 합집합 : 임의 노드가 부모 노드가 됨

def union(a, b):
    x = find_set_pc(a)
    y = find_set_pc(b)
    parent[x] = y

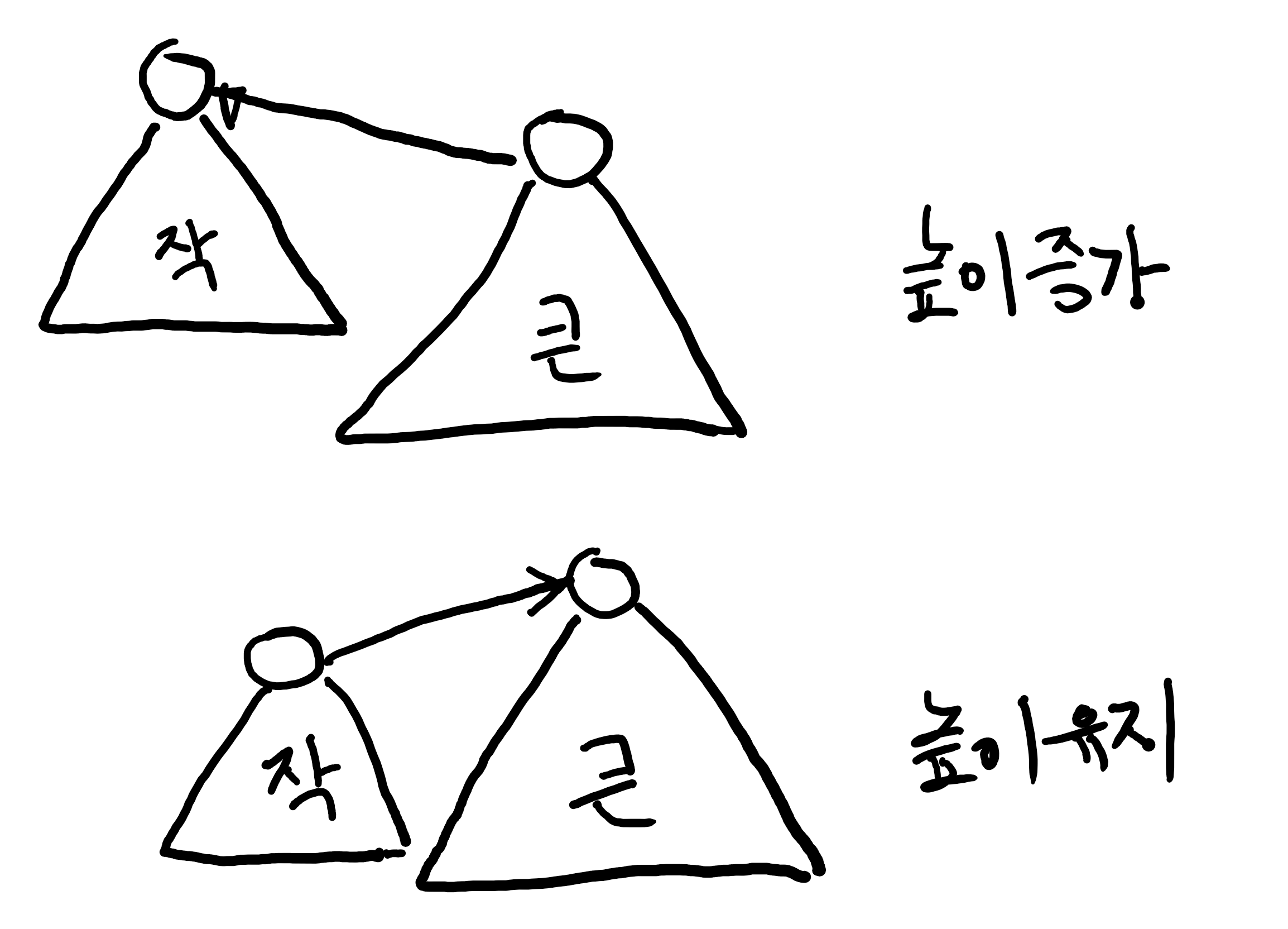
• weighted union
  • 사이즈가 큰 트리가 부모가 됨
  • 트리의 높이가 꼭 노드의 개수에 항상 비례하진 않음

def weighted_union(a, b):
    x = find_set_pc(a)
    y = find_set_pc(b)
    if size_list[x] > size_list[y]:
        parent[y] = x
        size_list[x] += size_list[y]
    else:
        parent[x] = y
        size_list[y] += size_list[x]

느낀 점

• MST 알고리즘 중 크루스칼 알고리즘 사용
• 노드개수 N, 에지개수 M이라 할 때
• Prim 알고리즘은 시간복잡도가 O(N**2) 이다
• 크루스칼 알고리즘은 O(Mlog2(M)) 이다
• 에지 개수가 노드 개수보다 훨씬 클 때 Prim 알고리즘이 유리할 때도 있겠지만
• 웬만하면 크루스칼이 훨씬 좋을 것 같다
  • 이 문제에서도 N = 100,000, M = 1,000,000 이라 그럴 것 같다

코드

import sys


def init():
    ipt = sys.stdin.readline
    n, m = map(int, ipt().split())
    edge_list = [tuple(map(int, ipt().split())) for _ in range(m)]
    parent = list(range(n+1))
    size_list = [1] * (n+1)
    return n, edge_list, parent, size_list, 0, 0


def find_set_pc(x):
    if x != parent[x]:
        parent[x] = find_set_pc(parent[x])
    return parent[x]


def weighted_union(a, b):
    x = find_set_pc(a)
    y = find_set_pc(b)
    if size_list[x] > size_list[y]:
        parent[y] = x
        size_list[x] += size_list[y]
    else:
        parent[x] = y
        size_list[y] += size_list[x]
  

n, edge_list, parent, size_list, count, ans = init()
edge_list.sort(key=lambda x: x[2])
for a, b, c in edge_list:
    if count == n-2:
        break
    if find_set_pc(a) != find_set_pc(b):
        weighted_union(a, b)
        ans += c
        count += 1
print(ans)