CS - Memory Management - 1 / 2

YOOJUN·2023년 2월 14일

CS

목록 보기

11/18

Memory Management

메모리 접근을 위해서는 주소가 필요
주소는 Logical address(Virtual address) 와 Physical address가 있다.
프로세스 생성시 독자적인 주소 공간(Address space)가 생성되는데, 이 때 사용되는게 논리적 주소.
각 프로세스는 0번지부터 시작하고 CPU는 이 주소를 사용.
물리적 주소는 Memory에서 물리적으로 접근할 수 있는 주소로 메모리에 실제 올라가는 위치이다.
프로세스 - 논리적 주소, 메모리 - 물리적 주소
프로세스가 실행되기 위해서는 메모리에 프로세스가 올라가고, 논리적 주소가 물리적 주소로 바뀌어야 하는데 이를 주소 변환 또는 주소 바인딩이라고 한다.

Symbolic Address

프로그래밍은 직접 메모리의 주소에 관여하지 않고 변수의 주소나 변수로 데이터의 흐름을 제어한다.
이 때 사용하는 것이 Symbolic address이고, Symbolic address가 컴파일 될 때 숫자로 된 주소인 Logical address로 변환되고, 실행 될 때 물리적 주소가 필요하기 때문에 주소 변환이 이루어진다.
프로그래밍 - Symbolic address, 컴파일 - Logical address, 실행 - 주소 변환

주소 바인딩(Address Binding) - 주소 변환

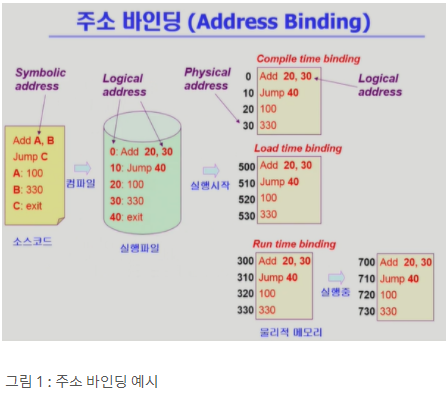
1. Compile time binding : 물리적 메모리 주소(Physical address)가 컴파일 시에 이루어지는 방법을 컴파일 타임 바인딩이라고 부른다.
1. Load time binding : 실행이 시작될 때 주소 변환이 이루어지는 것을 Load time binding이라 한다.
1. Execution time binding ( =Run-time binding) : 실행을 하는 도중에도 주소 변환이 이루어질 수 있는 방법을 Execution time binding이라고 한다.
  1. Compile time binding : 이제 이것이 실행이 되려면 메모리의 물리적인 주소로 올라가야 하고 이것을 주소 바인딩이라고 한다고 했다. 아까 전에 설명했던 Compile time binding은 앞서 논리적 주소라고 했던 숫자가 사실은 물리적 주소가 되는 것이다. 그렇기 때문에 컴파일러가 만들어 낸 코드는 절대 코드(absolute code)라고 불린다. 그래서 메모리에 올리고 싶은 위치를 바꾸고 싶으면 컴파일을 다시 해야 한다. 그러나 이 방법으로 주소 바인딩을 하는 것은, 뒤에 있는 주소들은 비었음에도 불구하고 0번지에 있는 주소부터 결정되기 때문에 비효율적인 방법이다. 옛날처럼 컴퓨터에서 하나의 프로그램만 실행할 수 있었던 경우에는 썼으나 최근 컴퓨터 시스템에서는 쓰지 않는다.
  2. Load time binding : 실행을 시작할 때 물리적 주소가 결정되는 방법이다. 메모리를 봤더니 500번지가 비어있으니 500번지에다가 논리적 주소 0번지부터 차례대로 올리라는 뜻이다. 컴파일러가 만들어낸 코드의 논리적 주소가 메모리 상황에 따라 바뀔 수 있기 때문에 컴파일러가 재배치 가능 코드(relocatable code)를 생성해야 한다.
  3. Run time binding : Load time binding과 비슷하게 실행 시 물리적 주소가 결정된다. 그러나 이 프로세스가 메모리에서 쫓겨났다가 다시 들어올 수도 있기 때문에 주소들이 실행 도중 바뀔 수 있게 된다.(Swapping) 이것이 Run time binding이다. 따라서 이 방법을 사용하면 CPU가 해당 프로세스의 주소를 참조할 때마다 binding을 Address mapping table을 이용하여 점검해야 하며 이를 위해 하드웨어적인 지원이 필요하다. 이때 사용되는 것이 MMU(Memory Management Unit) 혹은 base and limit register이다.

Memory Management Unit (MMU)

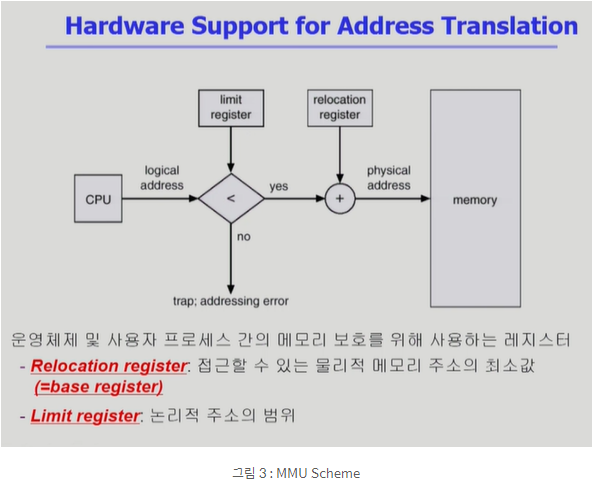
Run time binding을 이야기할 때 나왔던 장치. MMU는 Logical address를 Physical address로 매핑해주는 Hardware device.
MMU에서 주소 변환을 하는 방법은 기본적으로 레지스터 2개를 이용.

Appendix : 용어 설명

1. Dynamic Loading(동적 로딩)
  프로그램을 메모리로 올려야 실행이 될 것이다. Dynamic(동적으로) Loading(메모리로 올림)이란 프로그램을 전부 메모리에 올리는 것이 아니라 해당 루틴이 불려질 때마다 메모리로 올리는 것을 말한다. 여기서 말하는 동적 로딩과 OS에서 제공해주는 페이징과는 다른 개념인데 페이징에 대해서는 추후 설명하겠다. 원래 동적 로딩은 OS가 지원해주는 것이 아니고 프로그래머가 직접 동적 로딩을 하도록 만드는 것이다. 그 루틴들을 OS가 라이브러리 형태로 제공하여 프로그래머가 구현토록 한다. 그러나 요즘은 OS가 자체적으로 로딩을 제어하는 페이징 기법과 동적 로딩을 일종의 synonym으로 사용하기도 한다.
1. Overlays
  Overlay는 메모리에 프로세스 중에서 필요한 정보만을 올리는 것을 말한다. 이 내용만 봐서는 Dynamic Loading과 같다. 그러나 역사적으로 다르다. Overlay는 초창기 컴퓨터 시스템에서 워낙 메모리 크기가 작다 보니 프로그램 하나를 메모리에 올리는 것도 불가능했다. 따라서 프로그래머가 수작업으로 프로그램을 쪼개고, 이 부분이 필요하면 이 부분을 메모리에 올려놓고, 저 부분이 필요하면 저 부분을 메모리에 올려놓는 방식으로 구현하는 것을 Overlay라고 하며 Manual Overlay라고도 한다. 이것은 OS의 지원이 없고 사용자가 직접 모든 것을 구현해야 한다는 것이 Dynamic Loading과의 차이점이다.
1. Swapping
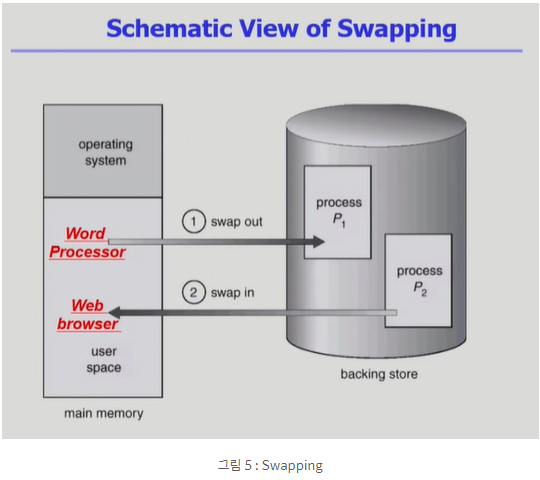
  메모리에 너무 많은 프로세스가 올라와 있으면 시스템이 비효율적이 되기 때문에 Swapping을 한다. 프로세스를 일시적으로 메모리에서 하드디스크의 Backing store로 쫓아내는 것을 말한다. Backing store는 Swap area라고도 부르며 많은 사용자 프로세스 이미지를 담을 만큼 충분히 빠르고 큰 저장 공간이다. 그래서 메모리에서 통째로 쫓겨나는 것을 Swap out이라고 하며, 쫓겨났던 프로세스가 메모리로 들어오는 것을 Swap in이라고 한다. 일반적으로 중기 스케줄러(초반에 배웠다. Swapper)에 의해 Swap out 시킬 프로세스를 결정한다. 주로 Priority-based CPU Scheduling Algorithm을 사용하기 때문에 priority가 낮은 프로세스를 Swap out 시키고 priority가 높은 프로세스를 Swap in 시킨다. 또한 Swap은 한 프로세스를 통째로 하드 디스크에 옮기는 것이기 때문에 방대한 양의 데이터가 이동된다. 따라서 Swap time은 당연하게도 하드 디스크에 접근하기 때문에 대부분이 transfer time-전송시간(Swap 되는 양에 비례하는 시간)이다.

Dynamic Linking

Linking을 실행 시간(Execution time)까지 미루는 기법. 프로그램을 작성하고 컴파일을 하면 목적 파일이 생성된다. 링킹이란 여러 군데 존재하는 목적 파일들을 묶어서 하나의 실행 파일을 만드는 과정을 뜻한다. 이때 필요한 라이브러리들이 실행 파일에 전부 포함되어 만들어지는데 이것을 Static Linking이라고 한다. 즉, 라이브러리가 프로그램 실행 파일 코드에 포함되고 이에 따라 실행 파일 크기가 커진다. 그러나 이 경우 동일한 라이브러리를 각각의 프로세스 메모리에 전부 올리기 때문에 메모리 낭비가 심하다. iostream이나 stdio.h와 같은 필수적인 라이브러리들은 중복으로 올라가게 될 것이기 때문이다.
반면 Dynamic Linking은 실행 파일에 라이브러리들을 포함시키는 것이 아니라 프로그램 실행 시에 라이브러리를 호출하는 곳에 도달했을 때 라이브러리를 연결하는 방법이다. 이때 라이브러리 호출 부분에 라이브러리 루틴의 위치를 찾기 위한 stub이라는 작은 코드를 둔다. 일종의 pointer 역할이다. 이때 라이브러리를 메모리에 올리게 되는데 만약 메모리에 해당 라이브러리가 이미 있다면 그 루틴의 주소로 가고, 메모리에 없다면 디스크에서 읽어오게 된다. 따라서 Dynamic Linking을 사용한다면 운영체제의 도움이 반드시 필요하다. 이 Dynamic Linking을 해주는 라이브러리를 Shared Library라고 부른다. 리눅스에서는 Shared Object, 윈도우에서는 dll이다.

Allocation of Physical Memory -물리적인 메모리를 어떻게 관리할 것인가?

메모리에서 낮은 물리 주소에는 운영체제 커널이 상주하고 높은 물리 주소 영역에는 사용자 프로세스 영역이 올라간다.
1. Contiguous allocation (연속 할당)
  각 프로세스가 메모리의 연속적인 공간에 통째로 적재되도록 하는 방법이다. 연속 할당에도 두 가지 방법이 있다.
1. Fixed partition allocation(고정 분할 방식)
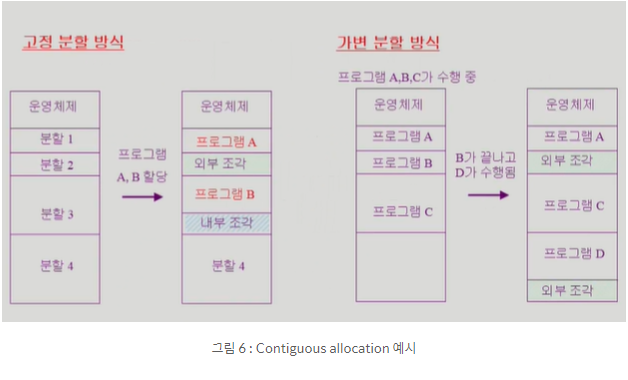
  고정 분할 방식이란 프로그램이 들어갈 물리적인 메모리의 사용자 프로세스 영역을 미리 파티션으로 나누어 놓는 것이다. 여기서는 사용자 프로세스가 올라갈 영역을 4개로 나누어 놓았다. 프로그램 A가 실행이 되고 마침 분할 1에 들어갈 수 있다면 거기에 로드하면 된다. 그런데 프로그램 B가 실행이 된다면 분할 2에는 들어갈 수 없기 때문에 분할 3에 들어간다. 그때 낭비되는 메모리 조각이 발생한다.
  1. External fragmentation (외부 조각) : 프로그램 크기보다 분할의 크기가 작아서 다른 분할로 들어가야 할 때 분할 한 개가 통째로 비어버리는 상황이 발생할 수 있다.
  2. Internal fragmentation (내부 조각) : 프로그램 크기보다 분할의 크기가 큰 경우 생기는 조각을 말한다.
  3. Variable partition allocation(가변 분할 방식) : 가변 분할 방식은 굳이 분할의 크기를 나누어 놓을 필요가 있겠는가 하는 의문에서 나왔다. 따라서 가변 분할 방식은 프로그램이 실행될 때마다 메모리에 차곡차곡 로드하는 방법이다. 그런데 만약 밑의 예시에서 프로그램 B가 끝나고 프로그램 D가 수행되는데 B가 들어갔던 공간이 작기 때문에 그 공간에 들어가지 못하고 아래쪽에 들어가게 된다. 따라서 가변 분할 방식에서는 내부 조각 문제는 발생하지 않지만 고정 분할 방식과 비슷하게 외부 조각 문제는 발생할 수 있다.

이런 연속 할당에는 다음과 같이 Hole이 발생한다. Hole은 가용 메모리 공간을 뜻하는데 연속 할당 방법에서는 이 Hole들이 여러 곳에 흩어져 있게 된다. 따라서 이를 운영체제가 관리해야 하며 운영체제는 각 프로세스가 할당된 공간과 가용 공간(Hole)에 대한 정보를 저장하고 있어야 한다.

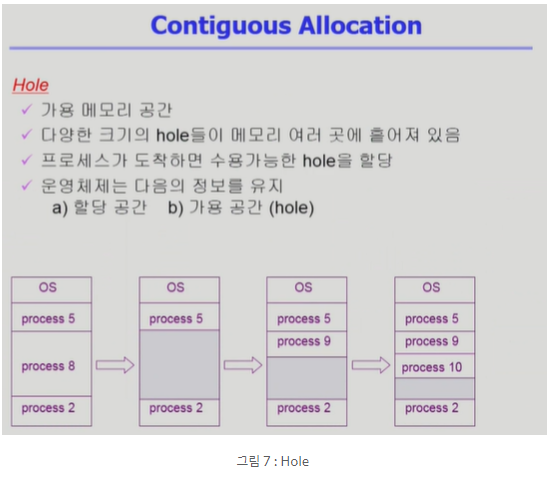
Dynamic Storage-Allocation Problem

이 가변 분할 방식에서 생기는 Hole 결정 문제를 Dynamic Storage-Allocation Problem이라고 한다. 지금 들어와야 하는 프로세스 사이즈가 n인데 hole이 여러 개일 때 가장 적절한 hole을 찾는 문제이다.
1. First-fit : Size가 n이상인 hole 중에 처음으로 찾아지는 hole에 집어넣는다.
2. Best-fit : Size가 n이상인 hole 중 가장 작은 hole에 할당을 하는 것이다. 그러나 hole들의 리스트가 크기 순으로 정렬되지 않았다면 모든 hole을 다 탐색해야 하며 많은 수의 아주 작은 hole들이 생성될 수 있다.
3. Worst-fit : Size가 n이상인 hole 중 가장 큰 hole에 할당하며 이 역시 모든 hole을 다 탐색해야 하고, Best-fit과는 반대로 상대적으로 큰 hole이 생성된다.

Compaction

외부 조각으로 발생하는 Hole들의 발생을 막기 위해 프로세스를 한쪽으로 전부 밀어서 큰 Block을 만드는 방법. 매우 비용이 많이 들며 최소한의 메모리 이동으로 Compaction 하는 방법은 매우 복잡한 문제이다. 또한 Compaction은 프로세스의 주소가 실행 시간에 동적으로 재배치 가능한 경우에만 수행될 수 있다(Run time binding).

Noncontiguous allocation (불연속 할당)

1. Paging
  프로세스가 구성하는 주소 공간을 같은 크기의 Page로 잘라서 Page 단위로 물리적인 메모리로 올려놓거나 Backing store에 내려 두거나 하는 것이다. 프로세스의 주소 공간을 자른 것처럼 물리적인 메모리에 사용자 프로세스가 들어갈 수 있는 공간들도 페이지와 똑같은 크기로 잘라 놓는데 이 물리적 공간을 Page Frame(페이지 프레임)이라고 한다. 이 Page Frame은 페이지 하나가 올라갈 수 있다. 이 기법을 사용하면 hole들의 크기가 균일하지 않아 발생하는 문제, External fragmentation(외부 조각 문제)가 발생하지 않는다. 물론 Internal fragmentation(내부 조각 문제)는 발생할 수 있다. 그 이유는 반드시 프로세스의 크기가 페이지 크기의 배수가 된다는 보장이 없기 때문이다. 추가적으로 Paging기법을 사용하면 MMU에 의한 주소 변환이 아니라 Page Table을 사용하여 주소 변환을 해야 한다.
기존에 연속 할당에서는 MMU의 register 두 개를 이용하여 주소 변환을 했다. 일반적으로 페이지 하나의 크기는 4KB이다보니 한 프로세스의 주소 공간을 페이지로 나누면 상당히 큰 숫자의 Page Table Entry가 필요하다. 그 큰 Entry들이 register안에 들어가지는 못할 것이다. 게다가 프로세스마다 Page Table이 별도로 존재해야 한다. 그렇다고 메모리 접근을 위한 주소 변환인데 어디 하드 디스크에 넣어둘 수도 없다. 또 캐시 메모리에 들어가기에도 Page Table들의 용량이 너무 크다. 따라서 Page Table을 메모리에다가 집어넣게 된다.
즉 Page Table은 main memory에 상주하게 되고, 앞서 MMU의 relocation register와 limit register는 Page Table을 가리키는 Page-table base register(PTBR)와 테이블의 크기를 보관하는 Page-table length register(PTLR)가 된다. 이러한 이유로 Paging 기법에서는 모든 메모리 접근 연산에는 2번의 memory access가 필요하다.

Effective Access Time (EAT)

실제로 메모리 접근 시간은 어떻게 계산되는가

Associative register lookup time = ε ( < 1)

memory cycle time = 1

Hit ratio = α (Associative register에서 찾아지는 비율)

EAT = (Associative register lookup time + memory cicle time) * Hit ratio + // 적다가 만 부분. 강의 들으면서 채우면 된다.

EAT = (1 + ε)*α + ( 2 + ε)*(1 - α) = 2 + ε - α

따라서 Page Table만 있을 때 걸리는 시간 2보다는 2 + ε - α가 훨씬 짧다.

Two-Level Page Table

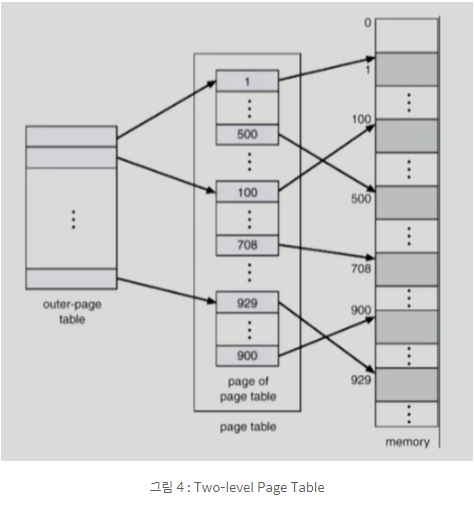
Page Table은 2단계로 존재할 수 있다. 여기서는 Outer-page table과 inner-page table이 있다. 페이지 테이블을 위한 공간이 줄어드는 것 때문에 2단계 페이지 테이블을 사용하는 것이다.
현대 컴퓨터는 Address space가 매우 큰 프로그램을 지원한다. 32 bit address를 사용한다면 2^32B (4GB)의 주소 공간을 표현할 수 있는데 Page size가 4KB이면 1M(1,048,576)개의 Page table entry가 필요하며, Page Entry 한 개의 크기가 4B 정도이기 때문에, 프로세스마다 4MB의 Page Table이 필요하게 된다. 그러나 대부분의 프로그램은 4GB의 주소 공간 중 일부분만 사용하기 때문에 Page Table 공간이 심하게 낭비된다. 이를 해결하고자 등장한 것이 2단계 페이지 테이블이다.
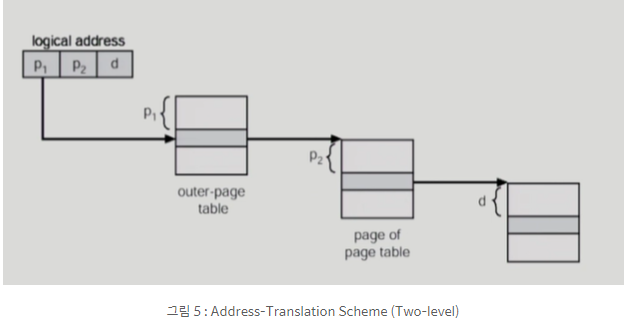
한 페이지에서 나타날 수 있는 변위는 최대 4KB이고 4K는 2^12이기 때문에 Offset을 나타내기 위해서는 12bit가 필요하다. 그리고 우리는 방금 Inner-Page Table에 Entry가 1K가 있다는 것을 알았다. 따라서 Inner-Page Table에서는 2^10의 서로 다른 Entry위치를 구분하기 위해 10bit가 필요하다. Outer-Page Table과 Inner-Page Table은 자연스럽게 10bit가 필요할 것이다.

Segmentation

세그먼테이션 기법은 프로그램의 주소 공간을 같은 크기로 자르는 것이 아니라 어떤 의미 있는 단위로 자르는 것. 대개 Code, Data, Stack 공간으로, 주소 공간을 세그먼트 별로 물리 공간에 올릴 수 있게 하는 것. 그러나 Segment의 크기가 균일하지 않기 때문에 앞서 살펴본 Dynamic Storage-Allocation Problem이 발생할 것이다.

===