
재귀함수란?

어떤 함수에서 자신을 다시 호출하여 작업을 수행하는 방식의 함수이다.
재귀함수 특징
반복문으로 구현할 수 있는 것은 재귀함수로 모두 구현이 가능하다.
재귀함수로 구현 가능한 것은 반복문으로 대부분(하지만 복잡..) 가능하다.
- 팩토리얼
function factorial(n){
if(n <= 1){
return n;
}
return n * factorial(n-1);
}
console.log(factorial(5));팩토리얼(!)을 재귀함수로 구현한 것이다.
factorial()함수에 5가 들어가면, if문을 만날 것이다.
5 > 1 이므로 5 factorial(5-1) 하며 factorial()함수를 다시 부른다.
이 과정을 반복하면 5 4 3 2 가 되며 이 값을 최종 return 한다.
- reverse
function reverse(text){
text += '';
if(text.length <= 1){
return text;
}
return reverse(text.slice(1)) + text[0];
}
console.log(reverse('abcd'));문자열을 역순으로 출력하기 위한 재귀함수다. reverse 함수를 호출하며 slice(1)로 알파벳 하나씩 앞에서부터 없애준다.
결과는 d + c + b + a 가 되어 'dcba'가 출력된다.
- 피보나치
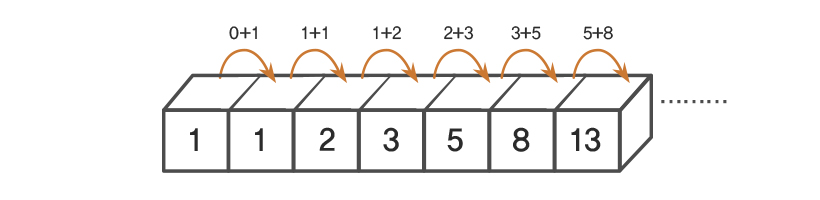
위키백과에 피보나치를 이해하기 위한 좋은 그림이 있다. 이것을 재귀함수로 짜보자.
function fib(n){
if(n <= 2){
return n;
}
return fib(n-1) + fib(n-2);
}
console.log(fib(4));fib(n-1) 부분
fib(4) == fib(3) + fib(2)
fib(3) == fib(2) + fib(1) == 3
fib(2) == 2
fib(1) == 1
fib(n-2) 부분
fib(2) == 2
fib(n-2) 부분에서 fib(2)를 다시 해야하는 상황이 발생했다. 만약에 수가 매우 커진다면 어떻게 될까? 효율이 매우 떨어지게 될 것이다.
그렇다면 fib(2) 같은 것을 기억해놨다가 다시 쓸수는 없을까?
// 호출되는 것이 메모리를 차지하고 있으므로 아래 기법을 적절히 믹싱해서 사용할 필요가 있음
// 반복문, 다이나믹 프로그래밍(메모이제이션(하향식), 타뷸레이션(상향식))
let fibo_cache = []
function fibo(n){
if (n in fibo_cache) {
return fibo_cache[n]
}
fibo_cache[n] = n < 2 ? n : fibo(n-2) + fibo(n-1)
return fibo_cache[n]
}
fibo(4)fibo_cache를 선언해 주었다. (저장했다가 불러와 사용하는것을 캐싱이라고 해서 변수명을 이렇게 지어주었다.)
재귀 동작
fibo(4) 이므로 fibo_cache[4] -> fibo(2) + fibo(3) -> 재귀중. 값 저장x
fibo(2)부분
fibo(2) 이므로 fibo_cache[2] -> fibo(0) + fibo(1) -> 재귀중. 값 저장x
fibo(0) 이므로 fibo_cache[0] -> 0리턴하면서 fibo_cache[0]에 값 저장
fibo(1) 이므로 fibo_cache[1] -> 1리턴하면서 ibo_cache[1]에 값 저장
fibo(2) 로 다시 가서 fibo(0) + fibo(1) 값 1을 저장.
fibo(3)부분
fibo(3) 이므로 fibo_cache[3] -> fibo(1) + fibo(2)
현재 fibo_cache에 0, 1, 2번째에 값이 저장되어있음.
그래서 fibo(3)은 fibo(1) + fibo(2) 값을 fibo_cache에서 바로 가져와서 1 + 1값인 2를 fibo_cache[3]에 저장.
최종적으로 fibo(4) 으로 돌아가서 fibo_cache에 저장된 fibo(2) , fibo(3) 값을 가져와 fibo(1) + fibo(2) 연산을 수행. 이것을 fibo_cache[4] 에 저장하는것이다. 그리고 이것을 리턴하는것으로 함수는 끝난다.
마무리
다이나믹 프로그래밍 메모이제이션을 마지막 예제에서 알아보았다.
삼항연산자 부분에서 fibo(n-2) 와 fibo(n-1)을 연산할 때 무엇을 앞에 놓을지는 메모리상 어느것이 이득인지 따져보면 된다. 이것은 스택과 힙을 알고있으면 이해하기 쉬울 것이다. 다음에는 스탭과 힙, 각종 정렬에 대해 알아보자.
