문제

N M의 칸에 `1 ~(N M)`의 수가 차례로 부여되어있다. 이때 최대 1칸에 O으로 표시가 된 구간이 있고 (없을 수 도 있음), 1번 칸에서 출발한 로봇이 아래, 오른쪽으로만 이동하면서 이 칸을 반드시 지나가야한다. 이러한 조건을 만족하면서 N * M 칸으로 이동할 수 있는 경로가 몇 개인지 계산하는 문제이다.

풀이

DP로 접근한 문제이고,
1. O가 없을 때

• (0,0)부터 (n-1, m-1)까지 경로의 수

2. O이 있을 때
   

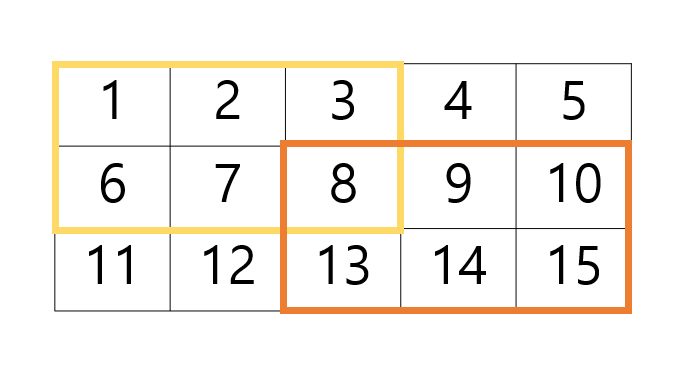
• (0,0)부터 O 좌표까지 경로의 수 (노란색)
• O좌표부터 (n-1, m-1)까지의 경로의 수 (주황색)
  를 구해서 이 둘을 곱했다.

경로 구하는 방식

각 칸마다 오른쪽, 아래로 이동하면서 이전까지의 경로 수를 더해주는 방식으로 구했다.

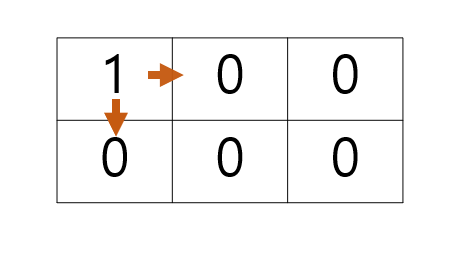
초기의 모습이다. (0,0)칸은 1부터 시작한다. 이때 주황 화살표로 표시된 구간에 이전 칸의 값인 1을 더해준다.

그럼 이와같은 모습이 됨.

그 다음칸도 동일하게 진행한다.

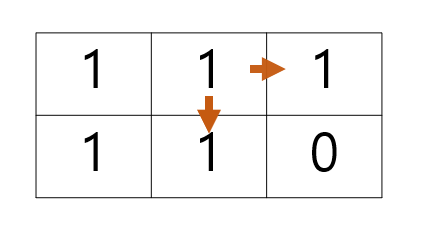
1행의 마지막 칸은 오른쪽으로 진행할 수 없으니 아래 칸에만 더해준다.

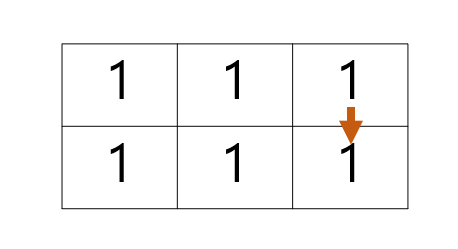
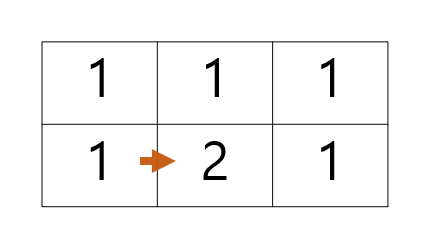
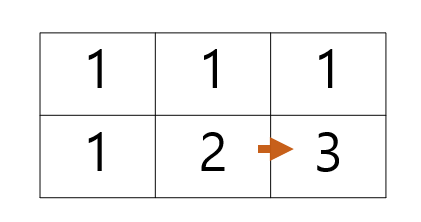
이렇게 쭉쭉 진행하면 맨 마지막 칸에는 최종 경로의 수가 저장된다.

소스 코드

import java.util.Scanner;

public class BOJ_10164 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int n = sc.nextInt();
        int m = sc.nextInt();
        int k = sc.nextInt();
        int answer = 0;

        if (k == 0) {
            answer = getRoute(n - 1, m - 1);
        } else {
            // O로 표시된 지점 좌표
            int x = (k - 1) / m;
            int y = (k - 1) % m;

            int firstRoute = getRoute(x, y);
            int secondeRoute = getRoute(n - x - 1, m - y - 1);

            answer = firstRoute * secondeRoute;
        }

        System.out.println(answer);
    }

    static int getRoute(int x, int y) {
        ++x;
        ++y;

        int[] dx = {0, 1};
        int[] dy = {1, 0};
        int[][] dp = new int[x][y];

        dp[0][0] = 1;
        for (int i = 0; i < x; i++) {
            for (int j = 0; j < y; j++) {
                for (int z = 0; z < 2; z++) {
                    int nx = i + dx[z];
                    int ny = j + dy[z];

                    if (nx >= x || ny >= y) {
                        continue;
                    }
                    
                    dp[nx][ny] += dp[i][j];
                }
            }
        }

        return dp[x - 1][y - 1];
    }
}

음 근데 지금 생각하니까 굳이 삼중 포문 안 돌려도 된다... 💦 좀 더 생각할걸 킥..
dp 배열의 칸을 한 칸씩 늘려서 선언해주고, dp[i][j] = dp[i-1][j] + dp[i][j-1]의 점화식으로 해결하는 방법도 있을 것 같다.