AIFFEL FD #10 머신러닝 알고리즘과 Scikit-learn

✅ 핵심 내용

• 머신러닝의 다양한 알고리즘 이해
• Scikit-learn 라이브러리 사용법
• Scikit-learn 을 통한 train, test 데이터 나누기

🤖 머신러닝(Machine Learning)

머신 러닝이란 말 그대로 기계가 학습을 통해 스스로 발전하는 것으로 인공지능(AI)의 수단 중 하나이다.

" 기계가 학습한다는 것은, 프로그램이 특정 작업(T) 을 하는데 있어서 경험(E) 를 통해 작업의 성능(P) 을 향상 시키는 것"

머신러닝의 알고리즘 종류는 크게 3가지로 나눌 수 있다.

• 지도학습(Supervised Learning)
• 비지도학습 (Unsupervised Learning)
• 강화학습 (Reinforcement Learning)

지도 학습은 "답" 이 있고, 이 답을 맞추는게 학습의 목적이다. 지도 학습에 속하는 대표적인 알고리즘은 다음과 같다.

지도 학습의 대표적인 알고리즘

분류 (Classification) : 예측해야할 데이터가 범주형(categorical) 변수 일때, 여러 카테고리 중 어느 카테고리에 속하는지 예측하는 것
회귀 (Regression) : 예측해야할 데이터가 연속적인 값일때, 연속적인 값 중 예측
예측 (Forecasting) : 과거 및 현재 데이터를 기반으로 미래를 예측

비지도 학습은 정해진 "답"이 없고, 유사한 데이터끼리 그룹화하는 등의 기능을 하는게 학습의 목적이다. 비지도 학습에 속하는 대표적인 알고리즘은 다음과 같다.

비지도 학습의 대표적인 알고리즘

클러스터링 : 특정 기준에 따라 유사한 데이터끼리 그룹화함
차원 축소 : 고려해야할 변수를 줄임

위의 알고리즘 말고도 다양한 알고리즘이 존재하고 정답 유뮤, 데이터의 종류, 특성 등에 따라 알맞는 알고리즘을 선택하여 사용하는 것이 중요하다.

강화 학습은 학습하는 시스템(에이전트)이 있고 환경(Environment)을 관찰해서 에이전트가 스스로 행동(Action)하게 한다. 그 결과로 특정 보상을 받고 이러한 보상(Reward)을 최대화하도록 학습하는 것이 강화 학습이다. 강화 학습에 속하는 대표적인 알고리즘은 다음과 같다.

강화 학습의 대표적인 알고리즘

Monte Carlo methods, Q-Learning, Policy Gradient methods

Scikit-learn 라이브러리를 통해 이러한 알고리즘들을 편리하게 구현할 수 있다. 또한 scikit-learn 에서는 데이터 수량, 라벨링 여부, 데이터 종류 등에 따라 어떠한 알고리즘을 선택해야하는지에 대한 가이드라인을 제시하고 있다.

➡ Chooing the right estimator by Scikit-learn

Scikit-learn 의 데이터 표현 방식

scikit-learn 에서는 보통 2가지로 데이터를 표현한다. 바로 특성 행렬 (Feature Matrix) 와 타겟 벡터 (Target Vextor) 이다.

특성 행렬은 입력 데이터를 행렬 형식으로 나타낸 것이고, 타겟 벡터는 입력 데이터의 라벨(답)을 의미한다. 즉, 타겟 벡터는 특성 행렬로부터 예측하고자 하는 것을 의미한다.

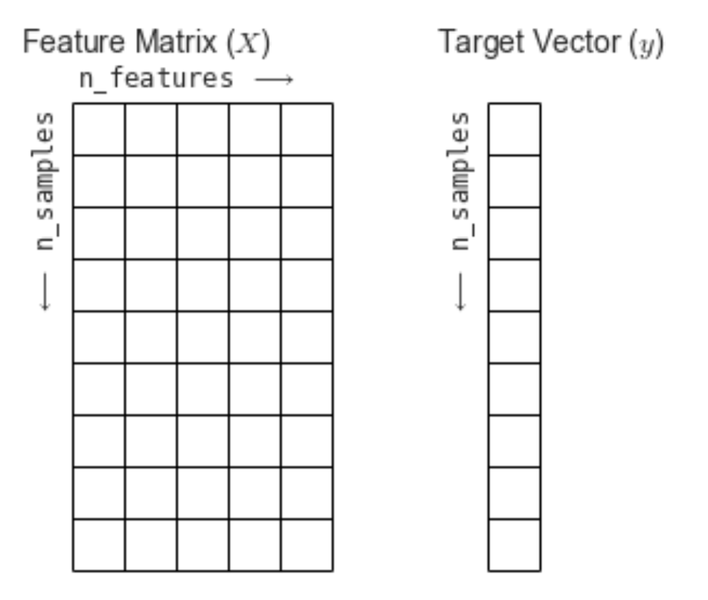
출처: https://jakevdp.github.io/PythonDataScienceHandbook/06.00-figure-code.html#Features-and-Labels-Grid

이러한 데이터 표현 방식을 가진 scikit-learn을 이용하여 여러 머신러닝 알고리즘을 구현해보자.

🌟 선형회귀 (Linear Regression)

scikit-learn 을 이용하여 머신러닝 알고리즘을 구현하기 전에 예전에 공부하였던 선형회귀의 기초에 대해서 당시 필기했던 내용을 바탕으로 복습을 하고 넘어가보자한다.

스토리텔링 식이니 과정에 맞게 순서대로 보면 재미있게 공부 할 수 있다.

일차함수의 개념인 y = ax + b 직선을 임의로 그려놓고, 그 직선을 바탕으로 예측을 하는 것이 선형회귀이다.

간단한 예로, 집 크기와 집 값이라는 데이터가 있고, 집 크기를 바탕으로 집 값을 예측해보려고 한다.

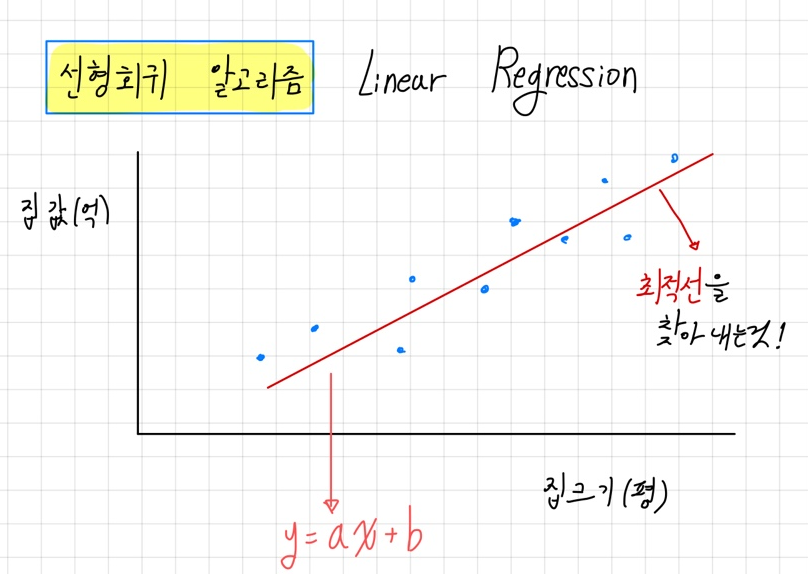
집크기를 x 라고 하고 집 값을 y라고 하여 $y= ax +b$ (a,b는 임의의 상수) 라는 직선을 만들수 있다.
그 후 a,b 값을 조정하여 최적선을 찾아내어 집 크기에 대한 집 값의 예측 값을 $y=ax+b$ 함수를 통해 구할 수 있다.

이러한 상수 a, b 를 조정하여 최적선을 찾아내는 과정을 선형회귀 라고 한다.

그리고 위의 예시에서 나온 집 크기를 입력변수 라고 하고, 집 값을 목표변수 라고 한다.

최적선을 찾기 위한 함수를 가설 함수 라고 한다. (위 예시에서는 $y=ax+b$)

일반적으로 가설 함수는 $h(x)= \theta _{0} + \theta _{1} x$ 로 나타낼 수 있다. ($\theta _{n}$ 은 상수, $x _{n}$ 은 입력변수)

$\theta _{0}$ 는 $b$ (bias, 편향)
$\theta _{1},\theta _{2},...,\theta _{n}$ 는 $w _{1},w _{2},...,w _{n}$ (weight, 가중치) 로 나타낼 수도 있다.

그렇다면 가장 적절한 $\theta$ 값들(최적선) 을 찾을 때 어떤 기준을 사용해야 할까?

이때 이용하면 개념이 평균 제곱 오차 (Mean Squared Error) 이다.

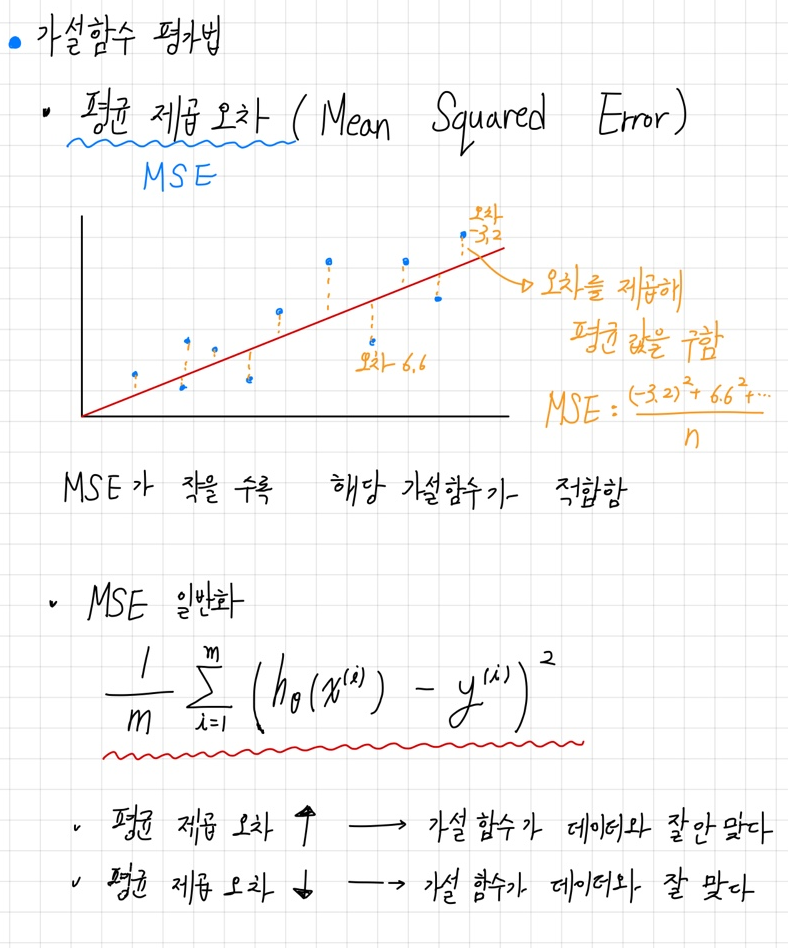
가설함수의 성능을 평가하는 함수를 손실함수 (Loss Function) 이라고 한다. 선형 회귀의 경우 손실함수는 MSE 이다. 즉, 선형 회귀의 손실 함수를 식으로 표현하면 아래와 같다.

$m$개의 데이터(입력변수, 목표변수) 에 대한 손실 함수를 $\theta _{0},..,\theta _{n}$ 에 대한 식으로 정리 할 수 있다. 이러한 $\theta$ 값들을 조정하여 손실 함수의 결과값을 최소화하는 것이 우리의 최종 목표인 가설 함수의 가장 적절한 $\theta$ 값들을 찾는 것이라고 할 수 있다.

그렇다면 어떻게 $\theta$ 값들을 바꿔 손실 함수의 결과값을 최소화 시킬 수 있을까?

바로 경사 하강법 을 사용한다.

경사 하강법이란 함수 값이 낮아지는 방향으로 독립 변수 값을 변형시키면서 최종적으로는 최소 함수 값을 갖도록 하는 독립 변수 값을 찾아가는 방법이다.

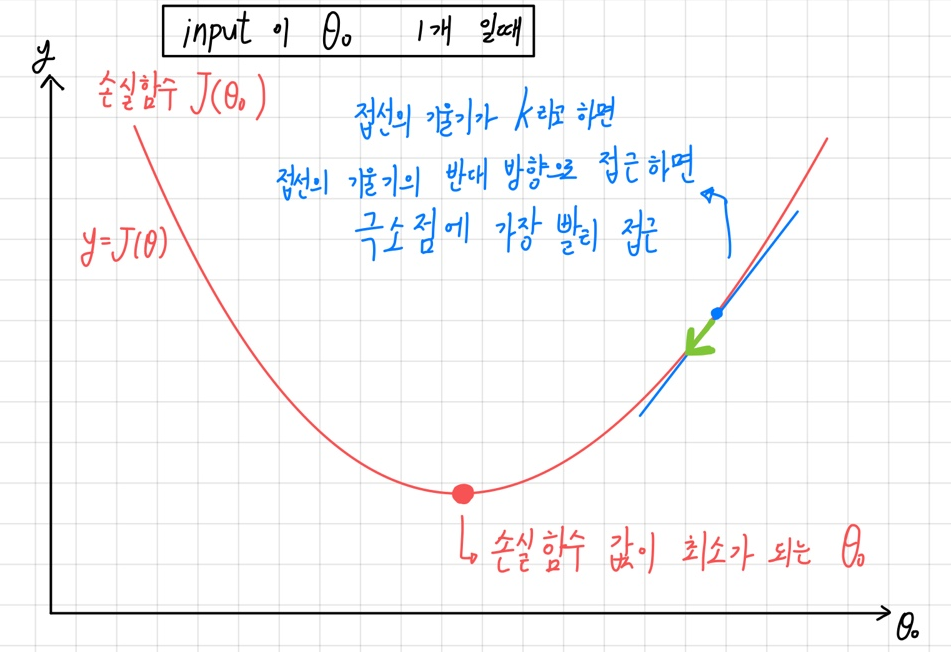
위의 그림처럼 접선의 기울기를 통해 극소점으로 가장 가파르게 내려가는 개념이 경사 하강법이다.

위의 예시처럼 가설 함수가 $h(x)= \theta _{0} + \theta _{1} x$ 인 경우, 해당 가설 함수의 손실 함수는 $J(\theta)$ 는 3차원의 그래프가 된다.
3차원의 그래프에서도 2차원의 그래프와 동일하게 한 점에서의 기울기의 반대 방향으로 내려가다보면 극소점 에 다다를 수 있다.

3차원 그래프에서 한점의 기울기를 구하는 법은 함수를 각 변수에 의해 편미분 후 결과식에 해당 점의 좌표를 대입하여 벡터 로 만드는 것이다.

이 후 기존의 한 점에서 그 기울기에 학습률(얼마나 많이 내려갈지 정하는것) 을 곱하여 경사 하강을 실시한다.

이 과정을 반복하면 극소점에 다다를수 있다.

위에 말한 과정을 일반화한 식은 다음과 같다.

지금까지 위에서 예시로 든 $h(x)= \theta _{0} + \theta _{1} x$ 의 가설 함수를 가지는 경우를 Linear Regressing 의 가장 기초적인 경우이다.

또한 선형 회귀 모델에서는 얼마나 예측을 잘하는지 평가 할때 평균 제곱근 오차(RMSE) 를 이용한다.

Scikit-learn 을 이용한 선형회귀

이러한 기초적인 선형회귀를 scikit-learn 을 통해 쉽게 구현 할 수 있다.

sklearn.linear_model 의 LinearRegression 을 이용하여 모델을 생성한다.

다음으로 sklearn.model_selection 의 train_test_split 을 통해 training set 과 test set 을 나눌수 있다.

이후 fit() 메소드를 이용하여 모델을 훈련시킨다.

마지막으로 predict() 를 메소드를 통해 예측값을 얻고 RMSE (평균 제곱근 오차)를 이용하여 모델의 성능을 평가한다.

RMSE를 이용하여 모델 성능을 평가할 때 쓰이는 함수는 mean_squared_error 이다.

자세한 과정은 아래의 GitHub 에 기록하였다.

GitHub Link 🔗 ➡ Linear Regression

---

🌟 다중 선형회귀 (Multiple Linear Regression)

위에서 설명 했듯이 하나의 독립 변수로 종속 변수를 예측하는 모델이 선형회귀 모델이다.

다중 선형회귀 모델은 여러 개의 독립변수를 가지고 종속 변수를 예측하기 위한 회귀 모델이다.

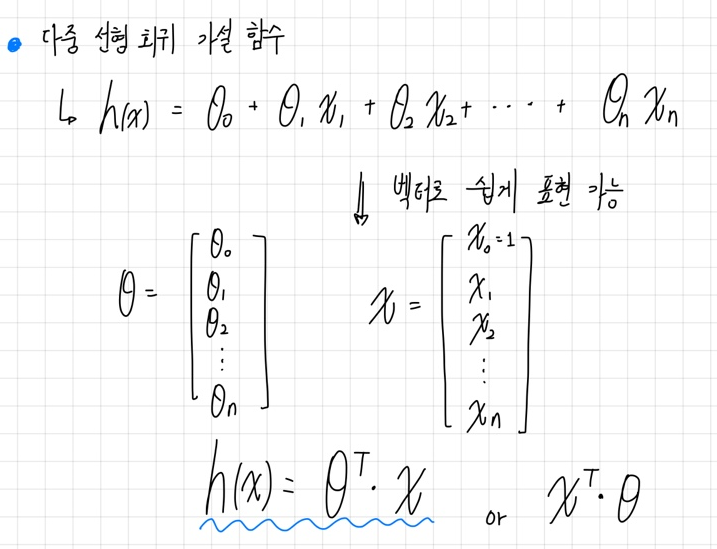
즉, 일반적인 다중 선형회귀 모델의 가설함수는
$h(x)= \theta _{0} + \theta _{1} x _{1} +\theta _{2} x _{2} +...+\theta _{n} x _{n}$ 의 형태이다.

이러한 형태의 가설함수는 벡터로 쉽게 표현이 가능하다.

Scikit-learn 을 이용한 다중 선형회귀

다중 선형회귀를 scikit-learn 을 통해 쉽게 구현 할 수 있다.

방법은 위에서 설명한 Scikit-learn 을 이용한 선형회귀 와 동일하게 진행하면 된다.

자세한 과정은 아래의 GitHub 에 기록하였다.

GitHub Link 🔗 ➡ Multiple Linear Regression

---

🌟 다항 회귀 (Polynominal Regression)

위에서 독립변수와 종속변수가 선형적인 관계인 경우에 선형 회귀 모델을 사용하여 예측하였다. 하지만 독립변수와 종속변수가 선형적인 관계가 아니라 곡선 형태로 되어있는 경우, 선형 회귀 모델을 사용하면 성능이 저하될 것이다.

다항회귀는 독립변수의 차수를 높이는 형태 이다. 다차원의 회귀식인 다항회귀 분석으로 선형 모델의 한계를 어느정도 극복 할 수 있다. 하지만 극단적으로 너무 차수를 높여서 모든 데이터를 지나게 한다면 overfitting(과적합)이라는 문제가 발생한다.

일반적인, 속성(독립변수)이 1개인 다항 회귀 의 가설 함수는
$h(x)= \theta _{0} + \theta _{1} x +\theta _{2} x^2 +...+\theta _{n} x^n$ 의 형태이다.

이러한 경우,
$h(x)= \theta _{0} + \theta _{1} x _{1} +\theta _{2} x_{2} +...+\theta _{n} x_{n}$ 형태의 다중 선형회귀와 동일하게 생각할 수 있다.

속성(독립변수)이 여러개인 다항 회귀 의 경우는, 기존 선형회귀에 새로운 속성을 추가해서 해결할 수 있다. 새로운 속성을 추가함으로써 복잡한 비선형 데이터 셋에 선형회귀에서 사용하던 방법을 그대로 사용할 수 있다.

예를 들어, 속성이 3개인 다항회귀를 하려고 할 때, 가설함수는 2차 함수라고 가정하면

$h(x)= \theta _{0} + \theta _{1} x _{1} +\theta _{2} x_{2} +\theta _{3} x_{3}+\theta _{4} x_{1}x_{2}+\theta _{5} x_{2}x_{3}+\theta _{6} x_{1}x_{3}+\theta _{7} x^2_{1}+\theta _{8} x^2_{2}+\theta _{9} x^2_{3}$

의 형태로 나타낼 수 있다. 이러한 경우는
$h(x)= \theta _{0} + \theta _{1} x _{1} +\theta _{2} x_{2}+\theta _{3} x_{3}+\theta _{4} x_{4}+\theta _{5} x_{5}+\theta _{6} x_{6}+\theta _{7} x_{7}+\theta _{8} x_{8}+\theta _{9} x_{9}$
형태의 다중 선형회귀와 동일하게 생각하여 해결 할 수 있다.

Scikit-learn 을 이용한 다항 회귀

속성이 여러개인 다항 회귀은 새로운 속성을 추가하여 선형회귀에서 사용하던 방법을 사용할 수 있다고 했다. Scikit-learn에서는 sklearn.preprocessing 의 PolynomialFeatures 함수를 통해 그러한 과정을 쉽게 구현할 수 있다.

PolynomialFeatures 을 통해 새로운 속성을 추가했다면 그 이후는 선형회귀와 동일한 과정으로 진행한다.

자세한 과정은 아래의 GitHub 에 기록하였다.

GitHub Link 🔗 ➡ Polynomial Regression

---

Scikit-learn 주요 모듈

위에서 다룬 선형회귀, 다항회귀 뿐만아니라 다양한 머신러닝 알고리즘이 존재한다.

scikit-learn은 여러 머신러닝 알고리즘과 많은 기능들을 쉽게 구현할 수 있도록하는 모듈들을 제공한다.

scikit-learn 의 주요 모듈을 아래에 정리했다.

	모듈명	설명
데이터셋	sklearn.datasets	scikit-learn 에서 제공하는 데이터셋
데이터 타입	sklearn.utils.Bunch	scikit-learn 에서 제공하는 데이터셋의 데이터 타입(자료형)
데이터 전처리	sklearn.preprocessing	정규화, 인코딩, 스케일링 등의 데이터 전처리
데이터 분리	sklearn.model_selection	train_test_split : 학습용,테스트용 데이터셋 분리
평가	sklearn.metrics	분류, 회귀, 클러스터링 알고리즘의 성능을 측정
머신러닝 알고리즘	sklearn.ensemble	앙상블관련 머신러닝 알고리즘 - 랜덤 포레스트, 에이다 부스트, 그래디언트 부스팅
	sklearn.linear_model	선형 머신러닝 알고리즘 - 릿지, 라쏘, SGD 등
	sklearn.naive_bayes	나이브 베이즈 관련 머신러닝 알고리즘
	sklearn.neighbors	최근접 이웃 모델 관련 - 릿지, 라쏘, SGD 등
	sklearn.svm	SVM 관련 머신러닝 알고리즘
	sklearn.tree	트리 관련 머신러닝 알고리즘 -의사결정 트리 등
	sklearn.cluster	군집관련 머신러닝 알고리즘