✅ 핵심내용
- 레이어 개념 이해
- 딥러닝 모델 속 각 레이어(Linear, Convolution)의 동작 방식 이해
- 데이터의 특성을 고려한 레이어 설계 및 Tensorflow 로 정의
데이터의 형태
딥러닝을 이해하는 방법 중 가장 쉬운 방법은 데이터의 형태 변화를 관찰하는 것이다.
간단한 예로,
- 10개 단어의 문장을 5개 단어로 요약 -> 정보 집약
- 10개 단어의 문장을 20개 단어로 확장 -> 정보를 더 세밀하게 표현
이미지 데이터는 보통 채널(Channel) 이라는 것을 가진다. 일반적으로 사용하는 RGB 이미지의 경우는 Red, Green, Blue 로 총 3개의 채널을 가진다.
표현 방식에 따라 Channel, Width, Height 의 이니셜로 (C, W, H), (W, H, C) 와 같이 표현가능하다.
간단한 예로, 해상도가 해상도가 1280 x 1024(30fps)이고 러닝타임(T)이 90분인 흑백 영화 데이터를 (T, C, H, W)에 따라 표현하면 (90*60*30, 1, 1280, 1024) 로 표현할 수 있다.
Linear 레이어
레이어 란?
하나의 물체가 여러 개의 논리적인 객체들로 구성되어 있는 경우, 이러한 각각의 객체를 하나의 레이어라 한다.
Fully Connected Layer, Feedforward Neural Network, Multilayer Perceptrons, Dense Layer 등 다양한 이름으로 불리는 모든 것들은 Linear 레이어에 해당한다.
Linear 레이어는 선형 변환(Linear Transformation)을 활용해 데이터를 특정 차원으로 변환하는 기능을 한다.
- 100차원의 데이터를 10차원으로 변환 -> 데이터를 집약시키는 효과
- 100차원의 데이터를 300차원으로 변환 -> 데이터를 더 풍부하게 표현하는 효과
예시 : 데이터 집약
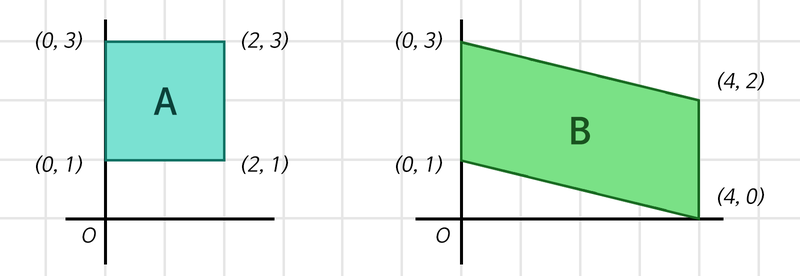
위 그림의 두 사각형은 모두 (x, y) 2차원의 점 4개로 표현 가능하므로, 각각 (4, 2) 행렬 형태의 데이터로 표현할 수 있다. 두 사각형을 각각 어떤 하나의 정수로 표현하고자 할때 아래의 단계를 사용한다.
- 1단계: (4, 2) x (2, 1) 행렬 = (4, ) ➡ 데이터 집약
- 2단계: (4, ) x (4, 1) 행렬 = (1, ) ➡ 데이터 집약

2차원을 1차원으로 변환하는 데에 (2, 1) 혹은 (2 x 1) 행렬이 하나 선언되고, 4차원을 1차원으로 변환하는 데에 (4, 1) 혹은 (4 x 1) 행렬이 하나 선언되고 각각의 행렬이 Weight 이다. 여기서 모든 Weight의 모든 요소를 Parameter 라고 한다.
이 과정을 코드로 표현한 것을 아래의 Github 에 기록하였다.
Github Link - FD20_Deep_Layer_Linear_Convolution
예시 : 데이터를 더 풍부하게 표현
첫 번째 접근은 데이터를 집약하는 데에만 집중했으니, 이번엔 데이터를 더 풍부하게 만들어보겠다.
- 1단계: (4, 2) x (2 x 3) 행렬 = (4, 3) ➡ 데이터를 더 풍부하게 표현
- 2단계: (4, 3) x (3 x 1) 행렬 = (4, ) ➡ 데이터 집약
- 3단계: (4, ) x (4 x 1) 행렬 = (1, ) ➡ 데이터 집약

1단계에서 2 x 3 = 6, 2단계에서 3 x 1 = 3, 3단계에서 4 x 1 = 4,
총 6 + 3 + 4 = 13개의 Parameter가 사용된 것을 확인할 수 있다.
Parameter 가 많은 것이 무조건적으로 좋다고 할 수는 없다. 지나치게 많은 Parameter는 과적합(Overfitting) 을 야기하기 때문이다.
이런 방법들로 Weight의 형태만 선언해주면 그 파라미터 값을 임의의 실수가 채우고, 수많은 데이터를 거치며 가장 적합한 Weight를 알아서 찾아가는 과정이 바로 훈련(Training) 이다.
이 과정을 코드로 표현한 것을 아래의 Github 에 기록하였다.
Github Link - FD20_Deep_Layer_Linear_Convolution
에서 는 편향 값(Bias)을 의미한다.
파라미터를 아무리 돌리고 늘리고 해도 정확하게 근사할 수 없는 상황에서 원점을 평행이동하는 것만으로도 해결할 수 있기 때문에 실제로 편향은 선형변환된 값에 편향 파라미터 b를 더해주는 것으로 표현한다.
위의 Github Link의 코드에서 Dense 클래스 속 use_bias 파라미터를 True 로 바꿔주면 편향값을 추가할 수 있다.
Convolution 레이어
Convolution 연산
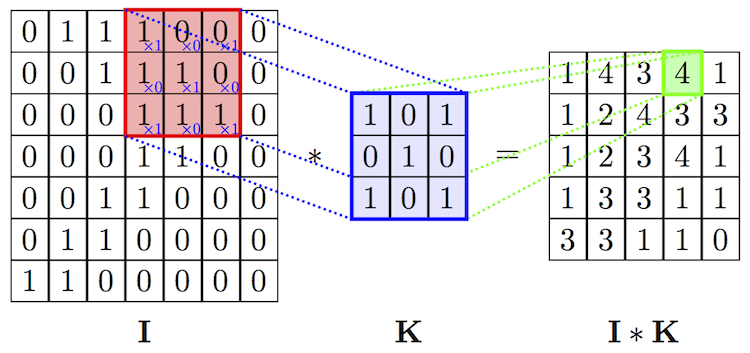
필터가 이미지와 겹쳐지는 부분의 Convolution 연산을 통해 새롭게 변환된 이미지 생성된다. 다양한 이미지 필터가 주는 Convolution 연산 효과를 아래 링크를 통해 시각적으로 확인할 수 있다.
필터(커널)를 선언한 후, 이미지를 필터로 훑으며 각 픽셀을 곱하여 더하는 Convolution 연산을 표현한다. 이때, 몇 칸 씩 이동하며 이미지를 훑을 지 결정하는 값을 Stride 라고 한다.
Convolution 연산이 이루어지면 Input 이미지가 작아진다. 이를 방지하기위해 Padding 을 이용한다. 입력의 테두리에 0을 추가해 입력의 형태를 유지할 수 있게 하는 테크닉이다. Padding 을 사용하면 모서리 부분의 중요한 정보도 활용할 수 있게 된다.
Convolution 레이어
Convolution 레이어는 수십 개의 필터를 중첩해서 해당 데이터와 목적에 적합한 Convolution 필터를 훈련을 통해 찾는 일을 수행한다.
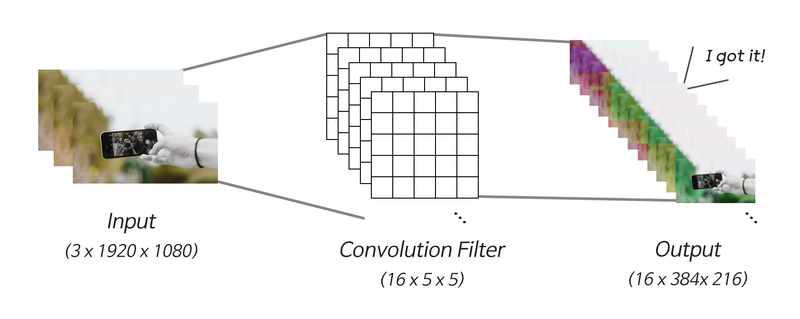
Convolution 레이어는 [ 필터의 개수 x 필터의 가로 x 필터의 세로 ] 로 이루어진 Weight를 갖는다
만약 1920*1080 의 컬러 이미지를 벡터로 나타내려고 할때,
- 1단계: (1920, 1080, 3) → (1920 x 1080 x 3, )
- 2단계: (6220800, ) x [6220800 x 1 Weight] = (1, )
위의 과정을 통해 약 620만개의 Parameter 가 생성된다. 이것을 효율적으로 하기 위하여 고안된 것이 Convolution 레이어 이다.
- 1단계: (1920, 1080, 3) x [3 x 16 x 5 x 5 Weight & Stride 5] = (384, 216, 16) ➡ Convolution 레이어
- 2단계: (384, 216, 16) → (384 x 216 x 16, ) ➡ 정보 집약
- 3단계: (1327104, ) x [1327104 x 1 Weight] = (1, ) ➡ 정보 집약
16개의 5 x 5 필터를 가진 Convolution 레이어를 정의하여 이미지를 Stride 5로 훑었고, 그렇게 생성된 출력을 1차원으로 펼쳐 Linear 레이어로 정보를 집약했다.
필터들은 입력의 3채널에 각각 적용되므로 Convolution 레이어의 파라미터는 3 x 16 x 5 x 5 = 1200개이다.
최종적으로 약 620만개의 Parameter 수를 Convolution 레이어를 통해 약 130만개로 크게 줄였다.
이 과정을 코드로 표현한 것을 아래의 Github 에 기록하였다.
Github Link - FD20_Deep_Layer_Linear_Convolution
Pooling 레이어
Receptive Field
Receptive Field(수용영역) 이란 외부 자극이 전체 영향을 끼치는 것이 아니라 특정 영역에만 영향 을 준다는 뜻 이다.
Neural Network의 출력부가 충분한 정보를 얻기 위해 커버하는 입력 데이터의 Receptive Field 가 충분히 커서 그 안에 detect해야 할 object의 특성이 충분히 포함되어 있어야 정확한 detection이 가능하다.
Max Pooling 레이어
Max Pooling 레이어를 통해 효과적으로 Receptive Field를 키우고, 정보 집약 효과를 극대화 할 수 있다.
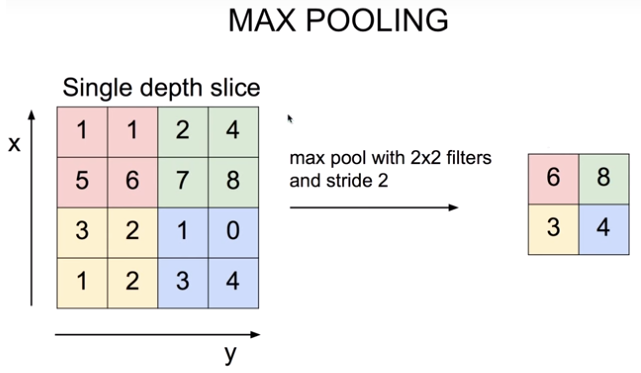
2 X 2 Max Pooling 레이어란 2 X 2 영역 안에서 가장 값이 큰 대표선수 하나를 뽑고 나머지는 무시하는 역할을 한다.
Max Pooling이 왜 좋은 것인지에 대한 설명을 아래 정리하였다.
- Translational Invariance 효과
- 이미지는 약간의 상하좌우 시프트가 생긴다고 해도 내용상 동일한 특징이 있는데, Max Pooling을 통해 인접한 영역 중 가장 특징이 두드러진 영역 하나를 뽑는 것은 오히려 약간의 시프트 효과에도 불구하고 동일한 특징을 안정적으로 잡아낼 수 있는 긍정적 효과
- object 위치에 대한 오버피팅을 방지하고 안정적인 특징 추출 효과
- Non-linear 함수와 동일한 피처 추출 효과
- Relu와 같은 Non-linear 함수도 마찬가지로 많은 하위 레이어의 연산 결과를 무시하는 효과
- 중요한 피처만을 상위 레이어로 추출해서 올려줌으로써 결과적으로 분류기의 성능을 증진시키는 효과
- Receptive Field 극대화 효과
- Max Pooling이 없이도 Receptive Field를 크게 하려면 Convolutional 레이어를 아주 많이 쌓아야함
- 그 결과 큰 파라미터 사이즈로 인한 오버피팅, 연산량 증가, Gradient Vanishing 등의 문제 발생
- 런 문제를 효과적으로 해결하는 방법으로 꼽히는 두 가지가 Max Pooling 레이어 사용, Dilated Convolution
Deconvoulution 레이어
Auto Encoder 는 Convolution의 결과를 역재생해서 원본 이미지와 최대한 유사한 정보를 복원해낼 수 있다.
MNIST 데이터셋을 입력으로 받아 그대로 복원하는 Auto Encoder 과정을 아래의 GitHub에 정리하였다.
Github Link - 추가 예정
Upsampling 레이어
정보를 복원하는 방법 3가지를 아래에 정리하였다.
- Nearest Neighbor : 복원해야 할 값을 가까운 값으로 복제한다.
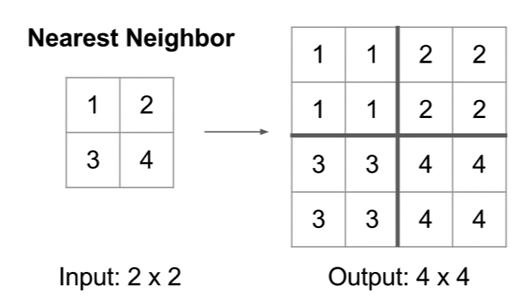
- Bed of Nails : 복원해야 할 값을 0으로 처리한다.
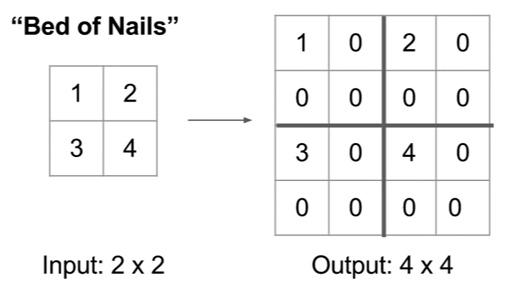
- Max Unpooling : Max Pooling 때 버린 값을 실은 따로 기억해 두었다가 그 값으로 복원한다.
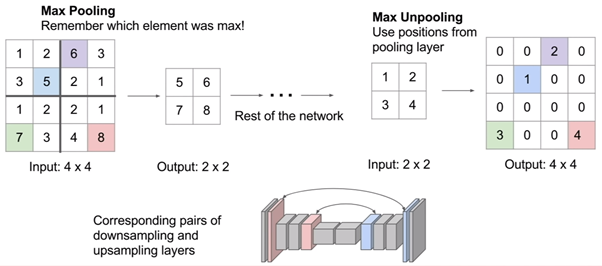
Transposed Convolution
이 과정을 코드로 표현한 것을 아래의 Github 에 기록하였다.
Github Link - FD20_Deep_Layer_Linear_Convolution
