https://arxiv.org/abs/1503.02531

0. Introduction

경량화 모델 중 증류하는 방법에 대해서 자세하게 살펴봅시다!
참고로 이 논문의 저자들은 세계적인 저자들이며 아직까지도 살아남은 논문이니만큼 읽어볼 가치가 충분히 있습니다!

제프리힌턴[노벨상 수상]

제프딘[구글최고리서처]
(제프딘의 29가지 진실 농담의 그 주인공 https://ppss.kr/archives/16672)

0.2 사전지식

(1) logit이란?

확률 $p$ 가 있다고 하자 .

여기서 $오즈(odds)$는 $\frac{p}{1-p}$=> 일어날 확률 vs 일어나지 않을 확률이다.
ex) 오즈(odds)가 3이라는 것은 일어날 확률이 일어나지 않을 확률보다 3배 높다는 의미

여기 odds에서 자연로그($ln$)을 취하면 logit값이 된다.
따라서 logit이란

즉, 로짓은 확률로 가기전 단계의 값이며 이 값을 바탕으로 시그모이드 또는 소프트맥스를 통해서 실제 확률이 계산.

(2) entropy란?

불확실성을 나타내는 수치

• 엔트로피가 높을수록 확률분포가 고르게 분산되어 있고 이는 불확실성이 큼
• 엔트로피가 낮을수록 확률분포가 한쪽에 치우쳐져 있고 불확실성이 낮음.

(3) Cross entropy란?

두 확률 분포 $p$와 $q$가 있을 때, $p$가 만들어낸 데이터가 사실이라고 하고, $q$가 그 데이터를 예측하려고 한다고 보면, 크로스 엔트로피 $H(p,q)$는 아래와 같이 정의됨

$H(p,q)$는 “진짜 분포(= $p$)를 따르는 데이터를 모델(= $q$)이 예측할 때 , 모델에서 예측한 확률값이 실제값과 비교했을 때 틀릴 수 있는 정보량.

만약 $p$와 $q$가 동일하다면, $H(p,p)=H(p)$가 되어 자기 자신에 대한 엔트로피가 된다.

$p$와 $q$가 다르면, $\sum_{x} p(x)\log q(x)$ 항이 작아져서 크로스 엔트로피 값이 커지게 된다.즉, $H(p,q)$가 높을수록 불일치가 크다는 말!

우리가 ‘진짜 분포’인 $p$를 one-hot 벡터(예: 정답 클래스에만 1, 나머지는 0)라고 가정하면, ‘모델의 예측 분포’인 $q$는 소프트맥스(softmax)로 나온 확률 벡터가 된다.

예를 들어, 분류 문제에서 $y$가 원-핫(one-hot)이고, $\hat{y}$가 모델이 예측한 확률 벡터라고 할 때,

가 자주 쓰이는 표준적인 손실 함수(Loss)가 된다.

1. Abstract

we show that we can significantly improve the acoustic model of a heavily used commercial system by distilling the knowledge in an ensemble of models into a single model

앙상블 모델을 활용하면 성능이 좋아지지만, 여러 대형 모델을 동시에 사용하기는 어렵다. 이를 해결하기 위해 앙상블 지식을 단일 모델에 증류(distillation)하는 방법이 제안되었다.

2. Introduction

대형(‘cumbersome’) 모델이나 앙상블 모델이 학습한 ‘지식(knowledge)’을 훨씬 가벼운 모델로 전이(distillation) 하는 방법을 소개

배경

큰 모델은 엄청난 데이터와 자원을 써서 뛰어난 일반화 능력을 갖추지만, 실제 서비스 단계(배포 단계)에서는 속도와 자원 제약이 크다.

핵심 아이디어

큰 모델이 예측할 때 생성하는 ‘소프트 타깃(soft targets)’—즉, 클래스별 확률 분포—을 작은 모델의 학습에 활용한다.

Temperature(온도)

소프트맥스의 온도를 높여서 작은 확률까지 더 두드러지게 만들어 주면, 큰 모델이 학습한 미세한 클래스 간 유사도 정보를 작은 모델로 효과적으로 전달할 수 있다.

장점

• 큰 모델이 가진 일반화 능력을 작은 모델이 모방할 수 있다.
• 작은 모델이기 때문에 계산량과 배포 비용이 훨씬 줄어든다.
• 원래 라벨과 함께 소프트 타깃을 혼합하여 학습하면, 실제 정답도 놓치지 않으면서 큰 모델이 배운 분류 경향을 그대로 이어받는다.

정리하면, distillation은 대형 모델이 발견한 풍부한 데이터 구조를 작은 모델로 효율적으로 전이해주는 기법으로 실제 서비스 단계에서 경량 모델을 사용하면서도 높은 성능을 유지하도록 돕는다.

3. Distillation

소프트맥스와 온도(Temperature)

• 신경망의 출력인 로짓(logit) $z_i$ 를 확률로 바꾸기 위해 소프트맥스를 사용한다.
• 소프트맥스에 온도 T를 적용하면 T가 클수록 ‘더 부드러운(분산된)’ 확률 분포가 만들어진다.
• 일반적으로 추론 시에는 T=1로 설정한다.
  $q_i = \frac{exp(z_i/T)}{\sum_j exp(z_j/T)}$

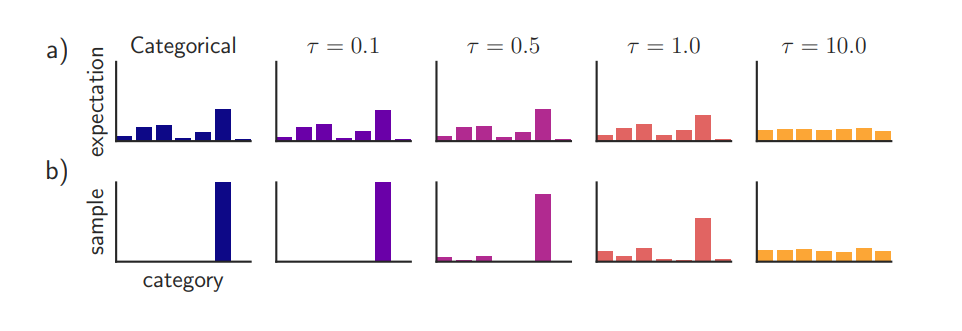
(Figure 1.) T($\tau$)가 높을 수록 불균등하게 expectation한다.

Temperature에 따른 softmax 확률값: https://arxiv.org/pdf/1611.01144

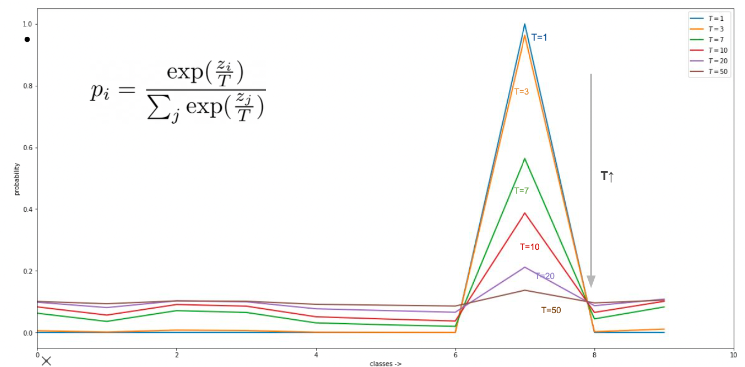
(Figure 2.) T가 높을수록 균등되는 확률이 고르게 분포됨을 알 수 있다.

(Gif 1.) Temperature에 따른 분포변화.

지식 증류(Knowledge Distillation)

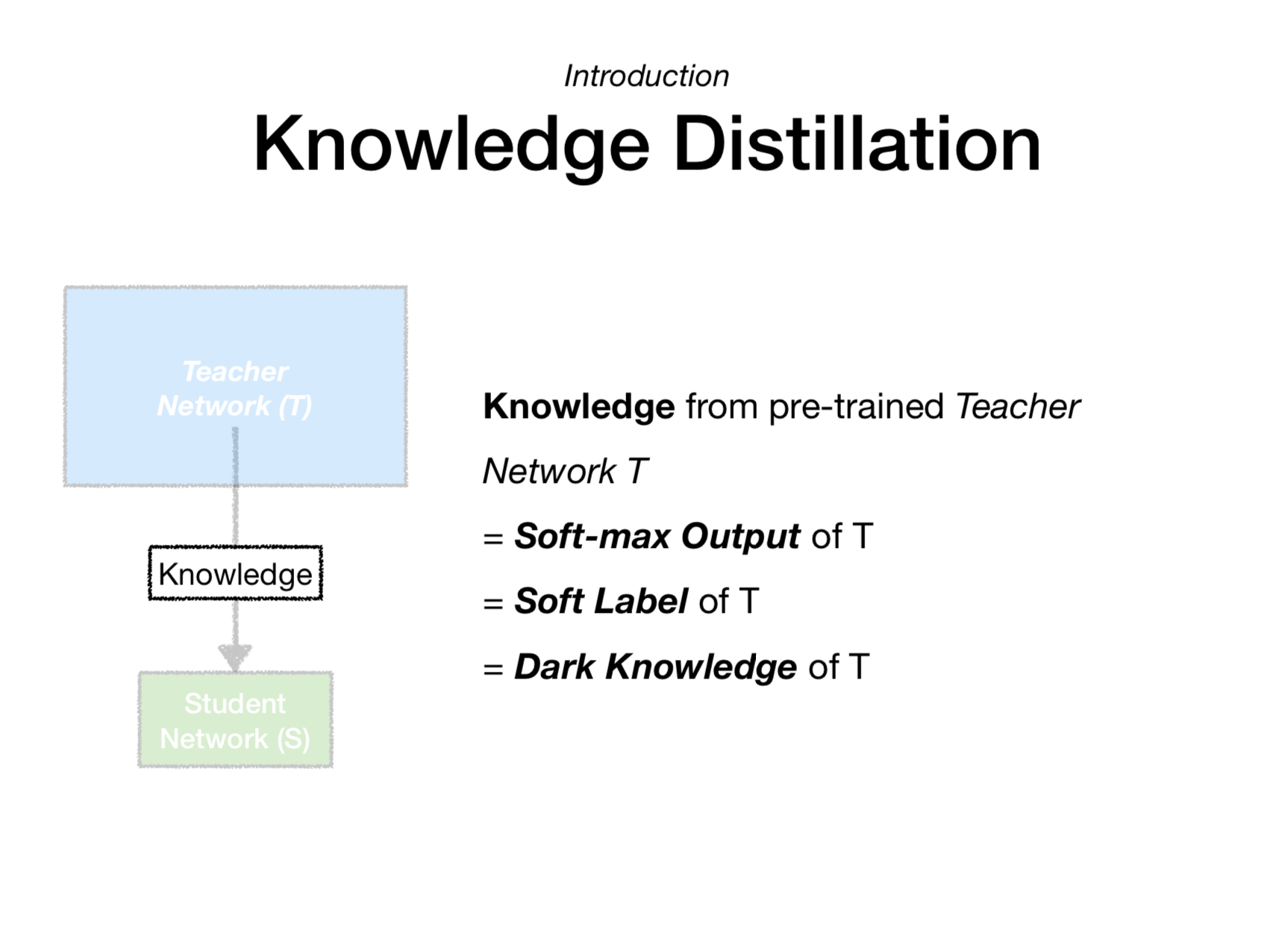
(Figure 3.) Knowledge Distillation 도식화.

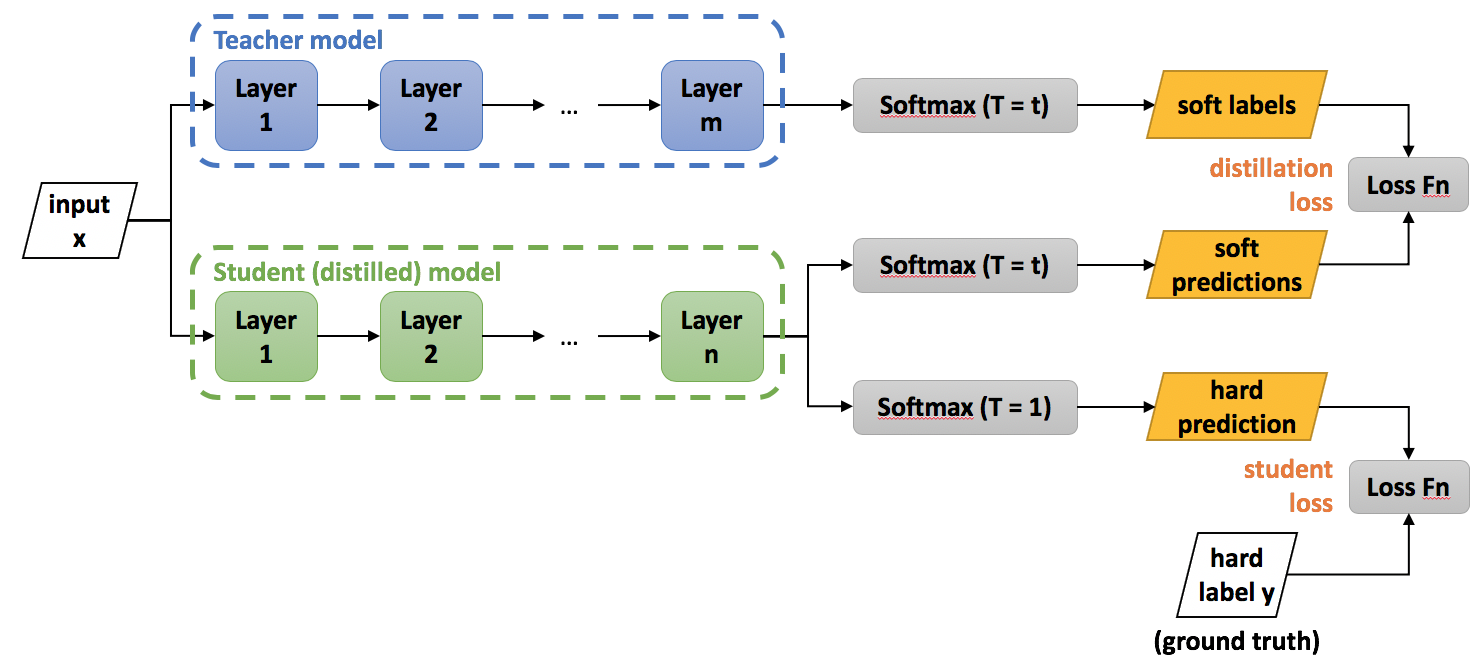
(Figure 4.) Knowledge distllation Loss 계산

3.1 Teacher 모델 (파란 박스)

입력($\mathbf{x}$)이 Teacher 모델에 들어가면, 여러 레이어(Layer 1, Layer 2, …, Layer m)를 거치면서 최종적으로 소프트맥스(Softmax) 출력을 낸다.

이때 소프트맥스의 온도 $T$를 크게 설정(예: $T > 1$)해주면, ‘부드러운’(soft) 확률 분포가 나오게 된다.

$z_i^{(\text{teacher})}$ 는 Teacher 모델의 로짓(logit) 값이며 $T$가 커질수록 한 클래스에 확률이 몰리지 않고 여러 클래스에 걸쳐 확률이 좀 더 고르게 분산된다.

이렇게 얻은 $p_i^{(\text{teacher})}$ (즉, 소프트 라벨(soft labels))은 Teacher 모델의 ‘지식’이 녹아 있는 확률 분포라고 볼 수 있다.

---

🤔 왜 teacher 에 $T$를 높여서 고르게 분포하게끔 하는 걸까?

👉 Knowledge Distillation에서는 Teacher 모델이 예측한 확률 분포가 단일 클래스에만 지나치게 몰리지 않고, 여러 클래스에 대한 상대적 중요도(“어느 정도 가능성이 있는지”)까지 학생(Student) 모델에게 전달되는 것이 중요하기 때문!

• T<=1 일 때의 소프트맥스는 가장 큰 logit을 갖는 클래스에 거의 모든 확률이 몰리기 쉽다.
• T>1 일 때는 분포가 더 부드럽게 되므로 정답 클래스 외의 다른 클래스들이 얼마만큼 있는지도 확률로 표현된다.

즉, 높은 T를 사용하여 Teacher가 산출하는 확률 분포를 부드럽게 만들어주면, Student 모델이 학습 시에 여러 클래스 간의 미묘한 확률 차이까지 참고할 수 있게 되어 Teacher 모델의 지식(“어떤 클래스들을 혼동하는지” 등)을 더 정교하게 학습할 수 있다!

(Figure 5.) Hard/soft 방식 차이.

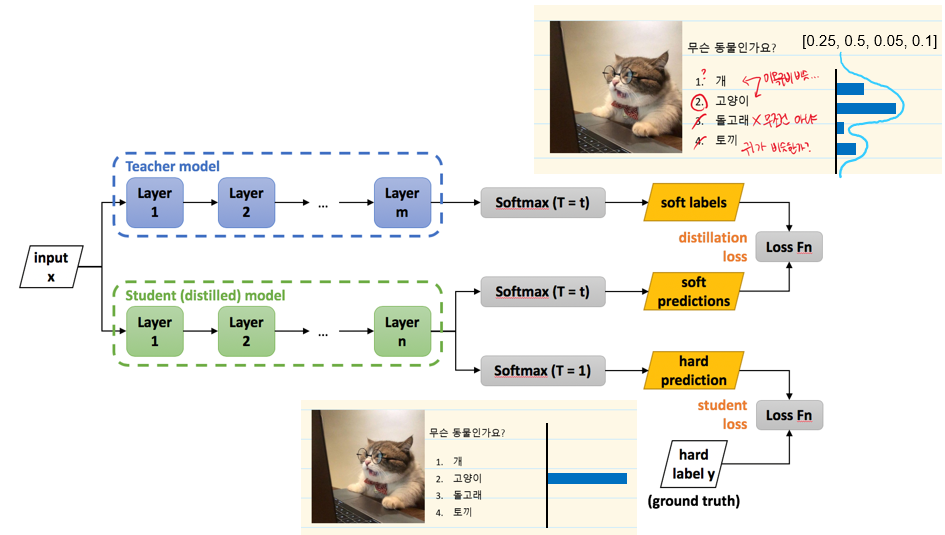
(Figure 6.) Knowledge distillation에 적용한 모습.

3.2 Student(혹은 Distilled) 모델 (초록 박스)

Student 모델은 보통 Teacher 모델보다 가벼운(파라미터가 적은) 구조로, Teacher 모델의 지식을 물려받아 유사한 성능을 내도록 설계한다.

같은 입력$\mathbf{x}$를 Student 모델에도 넣어 여러 레이어(Layer 1, Layer 2, …, Layer n)를 통과시킴.
Student 모델은 두 가지 소프트맥스를 동시에 계산할 수 있다.

Softmax (T = t)

여기서 $t$는 Teacher가 만들어낸 소프트 타깃 분포와 ‘가까워지도록’(distillation) 학습하려고 쓰는 출력이다.

Softmax (T = 1)

이 부분은 실제 예측을 위해 쓰는 일반적인 소프트맥스(온도 = 1).

3.3 Loss 함수(목적 함수)들

(1) Distillation Loss

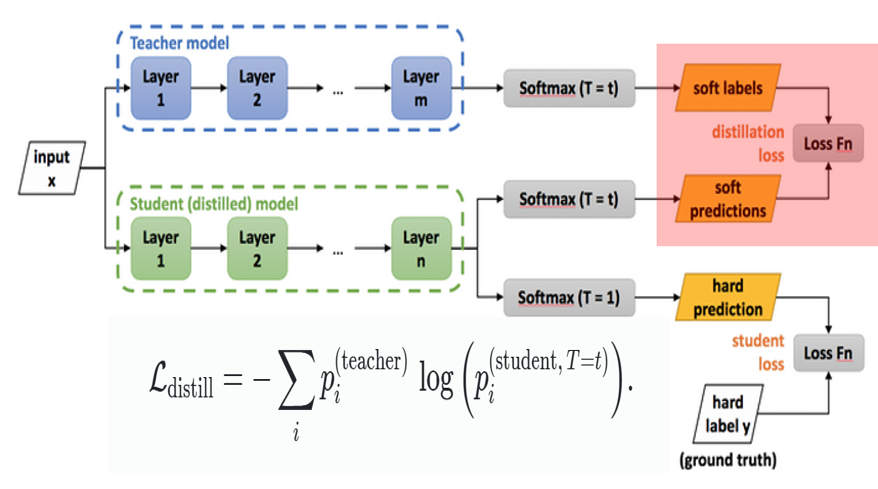
Teacher의 소프트 라벨 $p_i^{(\text{teacher})}$ 와 Student 모델의 소프트 예측 $p_i^{(\text{student},\,T=t)}$ 간의 크로스 엔트로피(Cross-Entropy)를 사용

이때 Teacher와 Student 모두 동일한 온도 $t$로 소프트맥스를 계산해야 부드러운 분포끼리 잘 맞출 수 있다.

또한, 소프트 타깃으로부터 오는 그래디언트가 $\frac{1}{T^2}$ 로 스케일 다운되므로, 일반적으로 $\mathcal{L}_{\text{distill}}$에 $T^2$를 곱해주는 방식(혹은 다른 방식으로 스케일 조절)을 적용

이렇게 해야 온도 $t$를 바꿔가면서 실험해도, 하드 라벨과 소프트 라벨의 상대적인 기여도가 크게 바뀌지 않는다.

왜 $T^2$을 곱해주는가?

지식 증류(Knowledge Distillation)에서 사용하는 온도(temperature) $T$는, 소프트맥스(Softmax)의 분포를 부드럽게(soften) 만들어 주는 역할을 한다. 수식으로는, 로짓(logit) $z_i$에 대해

와 같이 정의. 그런데 이때 크로스 엔트로피의 기울기(gradient)를 계산하면, 온도 $T$가 분포를 부드럽게 만들면서 $\frac{1}{T^2}$ 항이 등장해서 교사(Teacher) 분포와 학생(Student) 분포가 모두 같은 온도 $T$로 소프트맥스를 계산하면, 실제로 역전파(backpropagation)를 통해 학생 모델의 파라미터가 받게 되는 그래디언트가 $\frac{1}{T^2}$ 만큼 스케일 다운된다.

그러면 문제는 온도를 높여(예: $T > 1$) 분포를 더 부드럽게 만들면 학생이 받는 그래디언트가 그만큼 작아져서 모델이 잘 학습되지 않을 수 있다는 점입니다. 따라서, $\frac{1}{T^2}$로 감소한 그래디언트를 다시 $T^2$ 만큼 되돌려 주기 위해 아래와 같이 증류 손실($L_{\text{distill}}$)에 $T^2$를 곱해 주는 것이 일반적!

그렇다면 미분하는것 과정 보여주세요!

$L_{\text{distill}}$ 을 학생 로짓 $z_k$에 대해 미분하기

(1) $\log p_i(\text{student}, T)$를 먼저 미분
우선,

이를 $z_k$로 미분하면 다음과 같은 well-known 소프트맥스의 미분 공식이 적용되는데,

여기서 $\delta_{ik}$는 크로네커 델타($i=k$일 때 1, 아니면 0)입니다.
즉,

를 $z_k$로 미분하면

항이 생기고,

쪽에서도 체인 룰(chain rule)을 거쳐

항이 나옵니다.

(2) $\displaystyle L_{\text{distill}}$ 을 미분 (체인 룰)
이제,

를 $z_k$로 미분합니다. 체인 룰을 쓰면,

위에서 구한

를 대입하면,

이제

그리고

이므로,

결론적으로,

와 같이, 기울기(gradient)가

만큼 스케일 다운되어 나타납니다.

(2) Student Loss (Hard Label Loss)

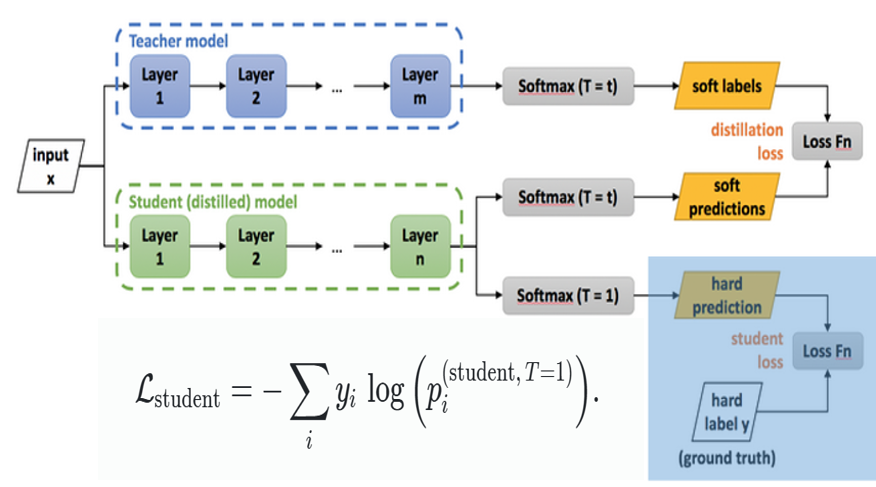
정답 라벨 $y$ (one-hot 형태)를 알고 있는 경우,Student 모델의 일반 소프트맥스 출력(온도=1) $p_i^{(\text{student},\,T=1)}$와 하드 라벨 $y_i$ 사이에 크로스 엔트로피를 사용

(3) 최종 결합

소프트 타깃과의 크로스 엔트로피(= $\mathcal{L}_{\text{distill}}'$)와 하드 라벨과의 크로스 엔트로피(= $\mathcal{L}_{\text{student}}$) 을 가중 합으로 섞어 사용한다.

3.4 Matching logits is a special case of distillation

🤔가장 적절한 온도값 $T$은 무엇일까?

3.4.1 증류(distillation)의 목표

• 복잡한 모델(“cumbersome model”)에서 나온 로짓(logits) $v_i$ 또는 확률분포 $p_i$를, 간단한 모델(“distilled model”)의 로짓(또는 확률분포) $\{z_i\}$가 잘 모사하도록 학습한다.
• 전이(transfer) 세트로 불리는 외부 혹은 추가 데이터에 대해, 복잡한 모델의 출력을 소프트 타겟으로 간주하고 이를 사용해 간단한 모델을 학습한다.

3.4.2 증류에서의 교차 엔트로피 오차의 그래디언트

• 식 (2)에 따르면, 복잡한 모델 logits $v_i$로부터 나온 확률 $p_i$, 증류 모델 logits $z_i$로부터 나온 확률 $q_i$에 대해,

  $\frac{\partial C}{\partial z_i} = \frac{1}{T}(q_i - p_i)$

  로 주어진다. 여기서 (T)는 온도(Temperature)이다.

3.4.3. 온도가 높은 경우 ($T \gg 1$)의 근사

• 로짓 자체의 값이 온도에 비해 상대적으로 작다면,

  $q_i \approx \frac{1 + \frac{z_i}{T}}{N + \sum_j \frac{z_j}{T}}, \quad p_i \approx \frac{1 + \frac{v_i}{T}}{N + \sum_j \frac{v_j}{T}}.$

• 특히 각 로짓을 케이스별로 0-평균화$\bigl(\sum_j z_j = \sum_j v_j = 0\bigr)$한 경우,

  $\frac{\partial C}{\partial z_i} \approx \frac{1}{N T^2}(z_i - v_i). \tag{4}$

• 따라서, 고온($T \gg 1$)에서는

  $\frac{1}{2}(z_i - v_i)^2$

  를 최소화하는 것과 사실상 같아진다 (즉, MSE 형태와 동등).

3.4.4. 낮은 온도 ($T$가 작은 경우)

• 평균보다 큰 음수 로짓($z_i \ll 0$)을 맞추는 데에는 상대적으로 중요도가 줄어들어, 그런 로짓을 무시하거나 덜 학습하게 된다.

• 이는 복잡한 모델에서 잘 학습되지 않아 노이즈가 큰 “매우 음수 로짓”을 덜 고려하므로, 노이즈에 휘둘리지 않을 수 있다는 이점이 있다.

3.4.5. 하지만 ‘매우 음수 로짓’이 주는 정보

• 큰 음수값이 “모델이 강하게 배제하는 클래스(혹은 상태)에 대한 정보”를 나타낼 수도 있으므로, 이를 무시함으로써 잃는 정보가 있을 수 있다.

3.4.6. 결론적으로

• 증류 모델이 원본 모델의 모든 지식을 담기에는 너무 작은 경우(용량 부족)에는, 너무 낮지도 너무 높지도 않은 ‘중간’ 온도가 오히려 좋은 성능을 낸다.(We show that when the distilled model is much too small to capture all of the knowledege in the cumbersome model, intermediate temperatures work best which strongly suggests that ignoring the large negative logits can be helpful)

• 이는 “매우 음수 로짓”에 지나치게 신경 쓰지 않음으로써 노이즈에서 자유로워지는 효과와, 이 로짓들을 완전히 무시하지 않는 절충점이 최적임을 시사한다.

4. Relationship to Mixtures of Experts

MoE

                 ┌───────────────────┐
                 │   Input Data      │
                 └─────────┬─────────┘
                           │
                  ┌────────v────────┐
                  │  Gating Network │
                  │ (할당 확률 계산)│
                  └───────┬─────────┘
                          │
    ┌─────────────────────┴─────────────────────┐
    │                                           │
┌────v────┐                                 ┌────v────┐
│ Expert 1 │                                 │Expert N │
└──────────┘                                 └──────────┘
                     ... (다른 Expert들)

                          │
                          ▼
                  ┌──────────────┐
                  │   최종 출력   │
                  │ (Aggregator) │
                  └──────────────┘

• Gating Network가 예제를 입력받아, 각 예제를 어느 Expert에게 할당할지 확률(가중치)을 계산
• 각 Expert는 자신에게 할당된 예제들로 학습하며, 추론 시에는 Gating Network의 확률에 따라 가중된 예측 값을 출력에 반영
  -> Gating Network와 Experts가 서로 영향을 주고받으며 동시에 학습해야 하므로, 병렬화가 어렵고 구현 복잡도가 높아짐짐

KD

학습시

              ┌─────────────────────┐
              │     Training Data   │
              └───────────┬─────────┘
                          │
                          ▼
            ┌────────────────────────┐
            │  Generalist Model (G)  │
            │  (범용 모델 학습)       │
            └───────────┬────────────┘
                          │
                          ▼
            ┌────────────────────────┐
            │   혼동 행렬(Confusion) │
            │   -> 데이터 subsets    │
            └───────────┬────────────┘
                ┌───────┴────────┐
                │                │
                ▼                ▼
       ┌────────────────┐   ┌────────────────┐
       │ Specialist #1  │   │ Specialist #2  │
       │ (하위 집합1)    │   │ (하위 집합2)    │
       └────────────────┘   └────────────────┘
                   ... (필요 시 더 많은 Specialist)

추론시

               ┌───────────────────┐
               │   Input Example   │
               └─────────┬─────────┘
                         │
                         ▼
         ┌─────────────────────────────┐
         │  Generalist Model (G)       │
         │  (어떤 Specialist가 필요?)  │
         └───────────┬─────────────────┘
                     │
         ┌───────────▼───────────┐
         │  관련 Specialist들    │
         │  예: S1, S2만 사용     │
         └───────────┬───────────┘
                     │
                     ▼
            ┌────────────────────┐
            │   최종 예측(출력)  │
            └────────────────────┘

• Mixtures of Experts는 동시에 모든 Expert가 Gating Network와 서로 맞물려 학습하는 구조인 반면
• 여러 Specialist는 일단 범용 모델로 영역을 나눈 뒤, 전문가들이 병렬로 학습하고 추론 단계에서 필요 Specialist만 골라서 쓰는 방식

구분	Mixtures of Experts	여러 Specialist + Generalist
핵심 아이디어	- 게이트(Gating) 네트워크가 실시간으로 Expert 할당 - 상호 의존적 학습 구조	- 먼저 범용 모델로 영역(Subset)을 정의한 뒤 - 각 Specialist를 독립·병렬 학습
병렬화(Parallelization)	- 게이트와 Experts가 얽혀 병렬화 어려움	- 하위 영역만 정해지면 Specialist끼리 병렬화 쉬움
추론(Inference)	- 게이트가 각 Expert 가중치 계산 - Experts 결과를 종합	- Generalist가 필요한 Specialist만 골라 사용 - 여러 Specialist 출력 결합
장점/단점	- 실시간 최적 Expert 선택 가능 - 병렬성·확장성 한계	- 특정 영역 성능 개선 용이·확장성 높음 - 영역 분할이 적절치 않으면 효과↓

5. Code

###########################################
# Teacher Model (Pretrained & Larger)
###########################################
teacher_model = models.convnext_large(weights=models.ConvNeXt_Large_Weights.IMAGENET1K_V1)
teacher_model.classifier[2] = nn.Linear(in_features=1536, out_features=100)
teacher_model = teacher_model.to(device)
for param in teacher_model.parameters():
    param.requires_grad = False
teacher_model.eval()  # Teacher를 eval 모드로 두어 동일한 출력 보장



###########################################
# Student Model 
###########################################

# 혹은 MobileNetV3 (Large) 사용:
class StudentMobileNetV3(nn.Module):
    def __init__(self, num_classes=100, pretrained=True, variant='large'):
        super().__init__()
        if variant == 'large':
            self.model = models.mobilenet_v3_large(
                weights=models.MobileNet_V3_Large_Weights.IMAGENET1K_V1 if pretrained else None
            )
        else:
            self.model = models.mobilenet_v3_small(
                weights=models.MobileNet_V3_Small_Weights.IMAGENET1K_V1 if pretrained else None
            )
        
        # MobileNetV3의 마지막 FC 레이어 교체
        # mobilenet_v3_(large/small).classifier[3]가 마지막 Linear 레이어
        in_features = self.model.classifier[3].in_features
        self.model.classifier[3] = nn.Linear(in_features, num_classes)
    
    def forward(self, x):
        return self.model(x)
        

class LabelSmoothingCrossEntropy(nn.Module):
    def __init__(self, smoothing=config.label_smoothing):
        super().__init__()
        self.smoothing = smoothing

    def forward(self, logits, target):
        with torch.no_grad():
            true_dist = torch.zeros_like(logits)
            true_dist.fill_(self.smoothing / (logits.size(1) - 1))
            true_dist.scatter_(1, target.unsqueeze(1), 1 - self.smoothing)
        return torch.mean(torch.sum(-true_dist * F.log_softmax(logits, dim=1), dim=1))


# Label Smoothing 제거한 Cross Entropy
class SimpleCrossEntropy(nn.Module):
    def __init__(self):
        super().__init__()
    def forward(self, logits, target):
        return F.cross_entropy(logits, target)
    
# Distillation Loss 정의 (T, alpha 변경)
def distillation_loss(student_logits, teacher_logits, labels, T=config.T, alpha=config.alpha):
    hard_loss = base_criterion(student_logits, labels)
    soft_loss = nn.KLDivLoss(reduction='batchmean')(
        F.log_softmax(student_logits/T, dim=1),
        F.softmax(teacher_logits/T, dim=1)
    )
    return alpha * soft_loss * (T*T) + (1 - alpha) * hard_loss


base_criterion = LabelSmoothingCrossEntropy(smoothing=config.label_smoothing)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
scheduler = CosineAnnealingLR(optimizer, T_max=num_epochs)

# RandAugment 
train_transform = transforms.Compose([
    transforms.Resize((32,32)),
    RandAugment(num_ops=config.randaugment_num_ops, magnitude=config.randaugment_magnitude),
    transforms.RandomHorizontalFlip(),
    transforms.RandomCrop(32, padding=4),
    transforms.ToTensor()
])

-> 자세한 코드는 깃헙 참고!

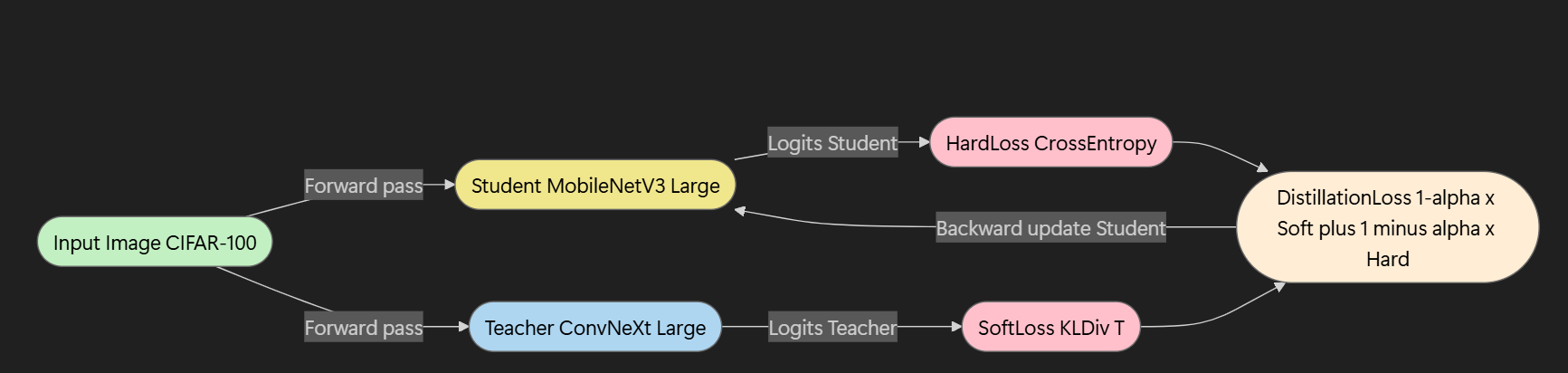
6. 실제성능테스트.

6.1 사용한 기법 및 모델 아키텍처

본 실험에서는 Knowledge Distillation(KD)을 활용하여 Teacher 모델로부터 Student 모델이 보다 효율적으로 학습하도록 유도하였다.

• Teacher 모델: ConvNeXt Large (ImageNet1K 사전학습 weights 사용)
  • ConvNeXt Large는 대규모 모델로, 높은 정확도를 가지나 연산량(참조: MFLOPs)이 커서 경량 환경에 직접 사용하기 어렵다.
• Student 모델: MobileNet V3 Large (ImageNet1K 사전학습 weights 사용)
  • MobileNet V3 Large는 경량화 모델로 알려져 있으며, Teacher에 비해 연산량이 훨씬 적어 실제 디플로이(deploy) 환경에서 유리하다.
• Distillation 구조:
  Teacher 모델의 출력을 soft target으로 활용하고, 이를 일정 온도(Temperature, T)로 부드럽게 만든 뒤 Student 모델에 전수(knowledge transfer)하였다. 이를 통해 Student 모델은 Teacher 모델이 학습한 복합적이고 부드러운 표현(distribution)을 흡수하여 적은 파라미터와 낮은 FLOPs로도 높은 성능을 달성할 수 있었다.

6.2 하이퍼파라미터 설정 및 최적화 과정

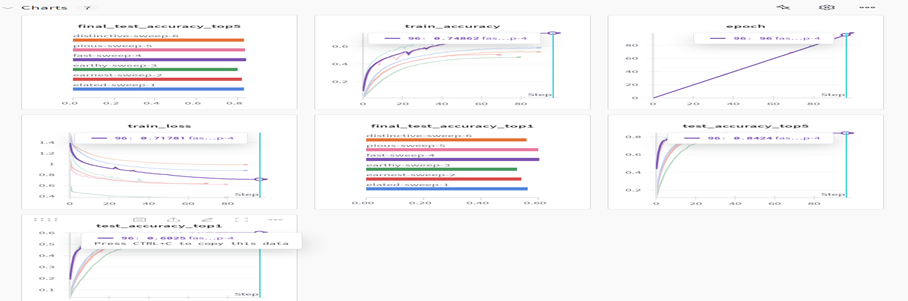
(Figure 1) wandb sweep을 통한 Hyperparameter 비교

에이전트들 중 가장 뛰어난 성능을 보인 fast-sweep-4(보라색) 에이전트를 선택하고, 그 에이전트의 하이퍼파라미터를 적용하였다.

• 학습률(learning rate): 0.0005, 에폭 수(num_epochs): 100
• 배치 크기(batch size): 256, Label Smoothing: 0.1 (단, 너무 큰 smoothing은 정보 손실 발생 가능)
• Knowledge Distillation 파라미터:
  • 알파(alpha)=0.7: Teacher 출력 소프트 로스 비중
  • 온도(Temperature, T)=5: Teacher의 soft target을 부드럽게 하는 정도
  • 데이터 증강(Data Augmentation): RandAugment 사용(num_ops=3, magnitude=11)

이러한 하이퍼파라미터 최적화 과정은 W&B(Weights & Biases)의 Sweep 기능을 통해 수행되었으며 (Figure 1 참조) Bayesian Optimization 기법을 사용하여 다차원 하이퍼파라미터 공간에서 효율적으로 최적의 조합을 탐색하였다. 이로써 반복적인 수동 튜닝을 최소화하고 시간 자원을 절약하면서 성능을 높일 수 있었다.

6.3 결과 비교 (Baseline 대비)

(Figure 2) MFLOPs 결과.

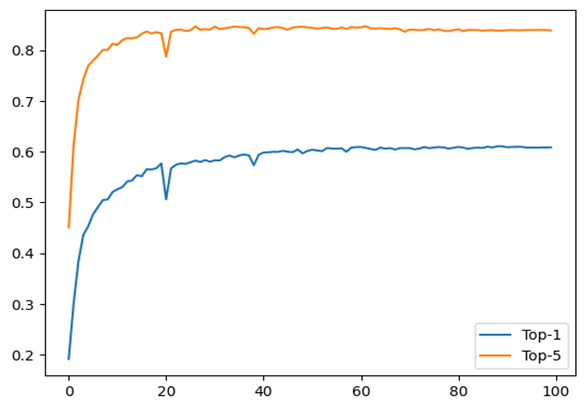
(Figure 3) test accuracy 차이와 Final performance 점수.

MFLOPs:

• 기존 모델 대비 약 42.71 MFLOPs에서 7.394976 MFLOPs로 대폭 감소
• 이는 약 82.7% ( (42.71 - 7.394976) / 42.71 * 100 ) 이상의 연산량 절감을 달성한 수치이다.

성능(Accuracy):

• 기존 Baseline 모델: Top-1 Accuracy = 48.8%, Top-5 Accuracy = 77.6%
• Distillation 적용 모델: Top-1 Accuracy = 60.3%, Top-5 Accuracy = 83.8%
  이를 통해 MFLOPs 대폭 감소와 동시에 Top-1 기준 약 11.5%p (48.8% → 60.3%), Top-5 기준 약 6.2%p (77.6% → 83.8%) 성능 향상을 확인할 수 있다. 즉, 연산량 절약과 정확도 상승이라는 두 마리 토끼를 잡는 데 성공하였다

항목	Baseline	Distillation	차이(증가/감소)
MFLOPs	42.71	7.394976	약 82.7% 감소
Top-1 Accuracy	48.8%	60.3%	+11.5%p (증가)
Top-5 Accuracy	77.6%	83.8%	+6.2%p (증가)