[자료구조]Graph Traversal이란?

지금까지 문제푸는 기계마냥 문제를 풀었다.. 하지만 이젠 그럴 수 업다!!!! 스터디 전 개념정리를 하고 문제를 풀어야겠다

---

📌 그래프 순회(Graph Traversal)란?

모든 정점을 방문하는 작업

그렇다면 생기는 의문!
😳시간복잡도가 너무 커지지 않나??

그래서 우리는 동일한 정점을 다시 방문하지 않도록 방문했다는 표시(visited)를 해 중복 방문을 피할 것이다.

그래프 순회 알고리즘엔 두가지 방식이 있다.
1. 깊이 우선 탐색(DFS: Depth First Search)
2. 너비 우선 탐색(BFS: Breath First Search)

🔍 깊이 우선 탐색(DFS: Depth First Search)

그래프에서 최단 경로를 찾는 edge기반 알고리즘
형제 정점을 탐색하기 전 child 정점부터 탐색함.

순서

1. 한 노드에서 시작
2. 엣지를 따라 다음 정점으로 방문
3. 더 이상 탐색할 간선이 없으면 역추적(backtracking)을 통해 이전 정점으로 이동하면서 탐색하지 않은 간선이 있는지 확인합니다.
4. 탐색 가능 간선이 있다면 다시 간선을 따라 다음 정점으로 이동
5. 모든 정점을 탐색할 때까지 3, 4를 반복함.

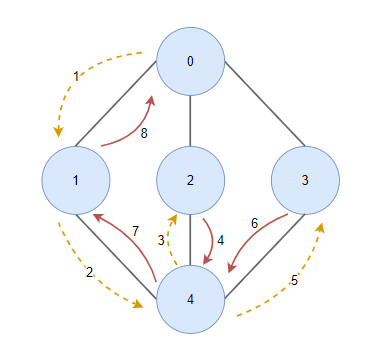
출처: https://yoongrammer.tistory.com/85

수행 과정

1. 시작 정점을 스택에 push
2. 스택의 맨 위에 있는 정점을 pop하고 방문 표시
3. pop된 정점에서 방문하지 않은 인접한 정점들을 스택에 push
4. 스택이 빌 때까지 2,3번을 반복

시간 복잡도

V = 노드의 수
E = 간선의 수
인접 리스트를 사용할 때 O(V+E)
인접 행렬을 사용할 때 O(V^2)

🔍 너비 우선 탐색(BFS: Breath First Search)

그래프에서 최단 경로를 찾는 정점 기반 알고리즘
자식 정점을 방문하기 전, 형제 정점을 방문함.

순서

1. 처음에 레벨 0에 있는 한 정점에서 시작
2. 레벨 1의 모든 정점을 방문(시작 정점에서의 거리 1)
3. 레벨 2의 모든 정점들을 방문(시작 정점에서의 거리 2)
4. 위와 같이 레벨을 늘려가며 모든 레벨의 노드들을 방문할 때까지 반복

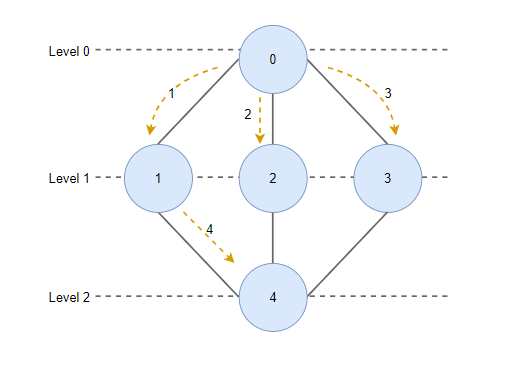
출처: https://yoongrammer.tistory.com/85

수행 과정

큐 자료구조를 사용하고, 큐는 한 레벨의 정점들을 저장하는 데에 사용.

1. 모든 정점을 방문하지 않은 상태로 표시
2. 시작 정점을 방문하여 방문 표시를 한 후, 큐에 삽입
3. 큐에서 첫 번째 정점을 제거하고 제거된 정점에서 방문하지 않은 인접한 정점을 방문하여 방문 표시를 한 뒤 큐에 삽입
4. 인접한 정점이 없는 경우 큐에서 첫번째 정점을 빼옴
5. 큐가 빌 때까지 3,4번을 반복

시간 복잡도(DFS와 동일)

V = 노드의 수
E = 간선의 수
인접 리스트를 사용할 때 O(V+E)
인접 행렬을 사용할 때 O(V^2)

---

📌 풀이방법은??

사실 위에서 떠는건 개념에 불과해서,, 막상 풀땐 별로 도움이 되지 않는다. 문제를 풀땐 바로 어떤 문제인지 파악이 필요하다!

DFS, BFS 둘 다 모두 그래프를 탐색하는 방법이다.
DFS는 자식 노드부터 방문, BFS는 인접 노드부터 방문 이라는게 차이점인데 아직 나의 경우에는 확 와닿지 않는다. 그럼 정확한 차이점은 뭐고! 접근 방식은 어떻게 되는걸까

🔍 DFS(Depth First Search)

루트 노드에서 시작해 다음 분기로 넘어가기 전, 해당 분기를 완벽하게! 탐색하고 넘어가는걸 말함.

미로찾기를 생각하면 쉽다!
갈 수 있을때까지 쭉 가고, 길이 없다면 다시 이전 갈림길로 돌아가 다른 길을 탐색하는 것이 깊이 우선 탐색이다.

1. 모든 노드를 방문하고자 할 때 택하는 방법
2. DFS가 BFS보다 간단함.
3. 검색 속도 자체는 BFS에 비해 느림

🔍 BFS(Breadth First Search)

루트 노드에서 시작해 인접한 노드를 먼저 탐색하는 방법!
시작 정점으로부터 가까운 정점을 먼저 방문하고, 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법

주로 두 노드 사이의 최단 경로를 찾고 싶을 때, 이 방법을 선택함.
예를 들어 지구 상에 존재하는 모든 친구 관계를 그래프로 표현 후, 철수와 영희 사이에 존재하는 경우를 찾는 경우에

DFS는 모든 친구 관계를 다 살펴보아야 하지만,
BFS는 철수와 가까운 관계부터 탐색할 수 있다.

🔍 둘의 차이점

• DFS
  • 현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색
  • 스택 또는 재귀함수로 구현
• BFS
  • 현재 정점에 연결된 가까운 점들부터 탐색
  • 큐를 이용해 구현

🔍 문제 유형

⚠️그래프의 모든 정점을 방문하는 것이 주요한 문제 ➡️ DFS, BFS
DFS, BFS 상관 없음! 편한거 쓰기

⚠️경로의 특징을 저장해야 하는 문제 ➡️ DFS
ex) 각 정점에 숫자가 적혀 있고, a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안된다는 문제
위와 같이 경로마다의 특징을 저장해야 하면 DFS를 사용함!
BFS는 경로의 특징을 가지지 못하기 때문

⚠️검색 대상의 그래프가 큰 경우 ➡️ DFS

⚠️최단거리를 구해야 하는 문제 ➡️ BFS
미로 찾기 등 최단거리를 구해야 할 경우, BFS가 유리
깊이 우선 탐색은 처음 발견한 해답이 최단거리가 아닐 수 있지만, BFS는 현재 노드에서부터 가까운 거리라 처음 답이 최단 거리이기 때문!

⚠️검색 대상의 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다 ➡️ BFS

---

출처

https://yoongrammer.tistory.com/85
https://velog.io/@lucky-korma/DFS-BFS의-설명-차이점