해시 테이블(Hash table)

Juhwan Lee·2022년 3월 15일

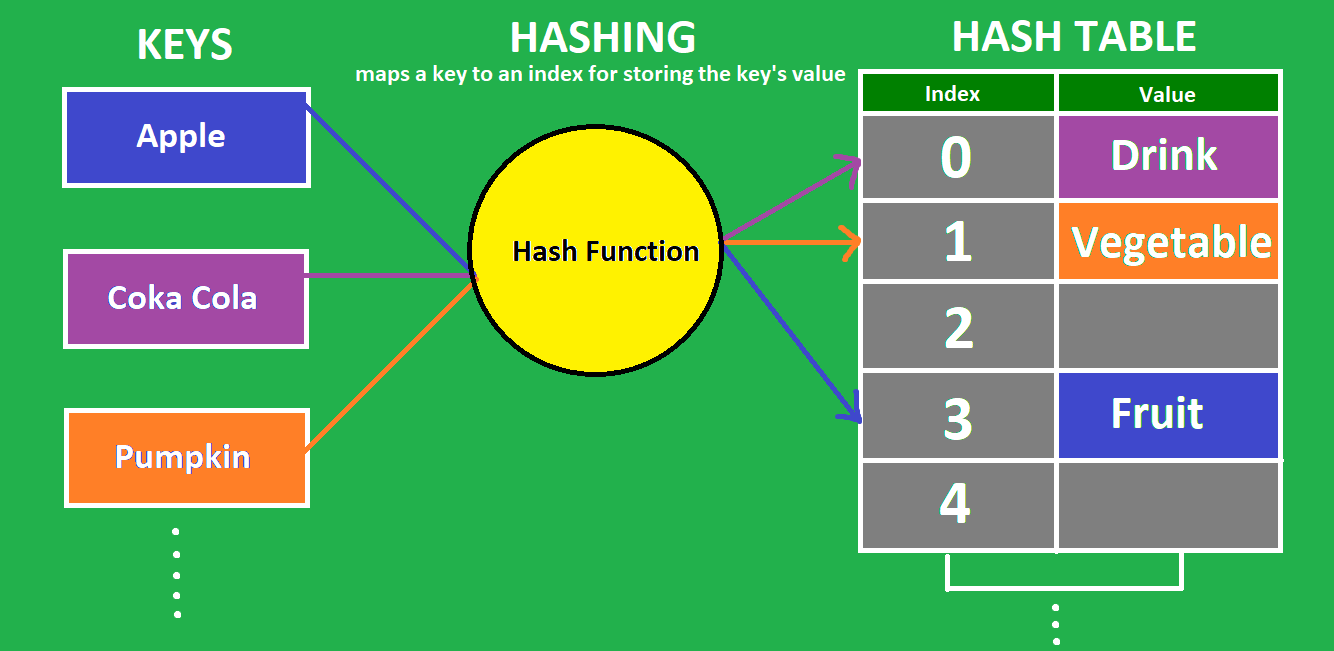
해시 테이블(해시 맵)은 키를 값에 매핑할 수 있는 구조인, 연관 배열 추상 자료형(ADT)을 구현하는 자료구조다.

가장 큰 특징은 대부분의 연산이 분할 상환 분석에 따른 시간 복잡도가 O(1)이라는 점이다. 덕분에 데이터 양에 관계 없이 빠른 성능을 개대 할 수 있다.

✍️ 해시

해시 테이블의 핵심은 해시 함수다.
해시 함수: 임의 크기 데이터를 고정 크기 값으로 매핑하는 데 사용할 수 있는 함수를 말한다.

❗ 특정 함수를 통과하면 고정 크기 값으로 매핑된다

정보를 가능한 한 빠르게 저장하고 검색하기 위해 사용하는 중요한 기법 중 하나다.
최적의 검색이 필요한 분야에 사용되며, 심볼 테이블 등의 자료구조를 구현하기에도 적합하다.

👍 성능 좋은 해시 함수들의 특징
1. 해시 함수 값 충돌의 최소화
2. 쉽고 빠른 연산
3. 해시 테이블 전체에 해시 값이 균일하게 분포
4. 사용할 키의 모든 정보를 이용하여 해싱
5. 해시 테이블 사용 효율이 높을 것

📍생일 문제

❗생각보다 충돌은 쉽게 일어난다

생일의 가짓수는 365개이므로, 여러 사람이 모였을 때 생일이 같은 2명이 존재할 확률을 얼핏 생각해보면 366명 이상이 모여야 일어나는 일 같지만, 실제로는 23명만 모여도 50%를 넘고, 57명이 모이면 그때부터는 99%를 넘어선다.

📍비둘기집 원리

왜 충돌은 일어날 수밖에 없을까?
비둘기집 충돌 원리를 보면, 간단한 귀류법으로 모순을 이끌어내 쉽게 증명할 수 있다.

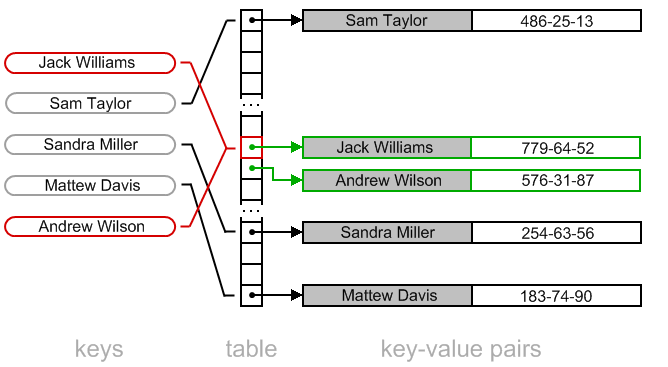
비둘기집 원리에 따라 9개의 공간이 있는 곳에 10개의 아이템이 들어온다면 반드시 1번 이상은 충돌이 발생하게 된다.
좋은 해시 함수라면 단 1번의 충돌이 일어나겠지만, 좋지 않은 해시 함수의 경우 심하면 9번 모두 충돌하게 된다.
여러 번 충돌한다면 그만큼 추가 연산을 필요로 한다.

📍로드 팩터

$load factor = \frac{n}{k}$
해시 테이블에 저장된 데이터 개수 n을 버킷의 개수 k로 나눈 것

로드 팩터 배율에 따라서 해시 함수를 재작성해야 될지 또는 해시 테이블의 크기를 조정해야 할지를 결정한다. 일반적으로 로드 팩터가 증가할수록 해시 테이블의 성능은 점점 감소한다.

📍해시 함수

해시 테이블을 인덱싱하기 위해 해시 함수를 사용하는 것을 해싱이라고한다. 해싱에는 다양한 알고리즘이 있으며, 데이터에 따라 최상의 분포가 제각각이다.

$h(x) = x$ mod $m$

x: 입력값

m: 해시 테이블의 크기(2의 멱수가 아닌 소수)

h(x): 이 값의 모듈로 연산의 결과

💣 충돌

❗아무리 좋은 해시 함수라도 충돌은 발생한다

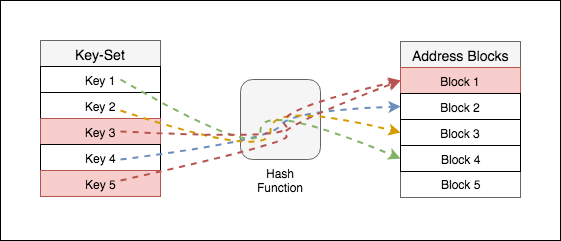
충돌이 발생할 경우 해결하는 방식을 살펴보자.

🔓 개별 체이닝

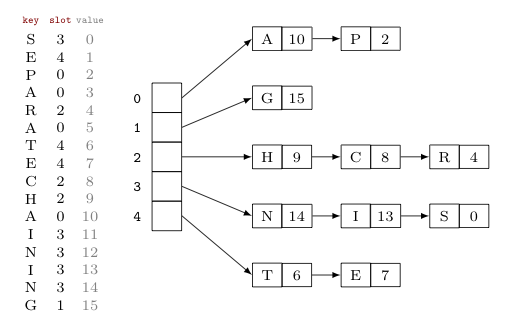
해시 테이블의 기본 방식이기도 한 개별 체이닝은 충돌 발생 시 이 그림과 같이 연결 리스트로 연결하는 방식이다.
이처럼 기본적인 자료구조와 임의로 정한 간단한 알고리즘만 있으면 되므로, 개별 체이닝 방식은 인기가 높다.

간단한 요약
1. 키의 해시 값을 계산한다.
2. 해시 값을 이용해 배열의 인덱스를 구한다.
3. 같은 인덱스가 있다면 연결 리스트로 연결한다.

🔓 오픈 어드레싱

충돌 발생 시 탐사를 통해 빈 공간을 찾아나서는 방식이다. 사실상 무한정 저아할 수 있는 체이닝 방식과 달리, 오픈 어드레싱 방식은 전체 슬롯의 개수 이상은 저장할 수 없다. 개별 체이닝 방식과 달리, 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장은 없다.

여러 오픈 어드레싱 방식 중에서 가장 간단한 방식인 선형 탐사 방식은 충돌이 발생할 경우 해당 위치부터 순차적으로 탐사를 하나씩 진행한다.

선형 탐사의 한 가지 문제점은 해시 테이블에 저장되는 데이터들이 고르게 분포되지 않고 뭉치는 경향이 있다는 점이다. 이러한 현상은 탐사 시간을 오래 걸리게 하며, 전체적으로 해싱 효율을 떨어뜨리는 원인이 된다.

오픈 어드레싱 방식은 버킷 사이즈보다 큰 경우에는 삽입할 수 없다. 따라서 일정 이상 채워지면, 즉 기준이 되는 로드 팩터 비율을 넘어서게 되면, 그로스 팩터의 비율에 따라 더 큰 크기의 또 다른 버킷을 생성한 후 여기에 새롭게 복사하는 리해싱 작업이 일어난다.

📍언어별 해시 테이블 구현 방식

Q. 해시 테이블로 구현된 파이썬의 자료형을 제시하라.
A. 딕셔너리 입니다!

파이썬은 개별 체이닝 방식이 아니다.
파이썬의 해시 테이블은 충돌 시 오픈 어드레싱 방식으로 구현되어 있다.

성능을 높이는 대신, 로드 팩터를 작게 잡아 성능 저하 문제를 해결한다. 파이썬의 로드 팩터는 0.66으로 자바보다 작으며 루비는 0.5로 훨씬 더 작다.

✍️ 파이썬으로 해시테이블 구현

# 리스트를 활용한 간단한 해쉬 테이블 구현

hash_table = list([0 for i in range(8)])  # 해쉬 테이블 공간 생성


def get_key(data):  # 해쉬 키 생성
    return hash(data)  # 내장함수


def hash_function(key):  # Division을 이용한 간단한 해쉬 함수
    return key % 8


def save_data(data, value):
    hash_address = hash_function(get_key(data))  # 해쉬 함수로 산출한 해쉬 주소
    hash_table[hash_address] = value


def read_data(data):
    hash_address = hash_function(get_key(data))
    return hash_table[hash_address]

위에 구현한 해쉬 함수는 데이터를 저장할 때 중복된 해쉬 주소가 생성될 경우(충돌), 데이터를 덮어써버리는 문제가 발생한다.

충돌 해결을 위한 방법
1. 연결리스트를 이용해 데이터를 추가로 뒤에 연결시켜 저장하는 기법 (Open hashing)
2. 충돌이 일어난 해쉬 주소의 다음 주소들 중 빈 공간에 데이터를 저장하는 기법 (Close Hashing)

📍Open Hashing

# Open Hashing 기법을 적용한 hash table (체이닝 기법)
hash_table = list([0 for i in range(8)])  # 해쉬 테이블 공간 생성


def get_key(data):  # 해쉬 키 생성
    return hash(data)


def hash_function(key):  # Division을 이용한 간단한 해쉬 함수
    return key % 8


def save_data(data, value):
    index_key = get_key(data)
    hash_address = hash_function(index_key)

    # 1. 해쉬 충돌이 발생할 경우 ( 해쉬 주소가 동일할 경우 )
    if hash_table[hash_address] != 0:
        for index in range(len(hash_table[hash_address])):
            # 1-1. key가 동일하면 데이터를 덮어 쓴다
            if hash_table[hash_address][index][0] == index_key:
                hash_table[hash_address][index][1] = value
                return
        # 1-2. key가 동일하지 않으면 데이터를 연결해 저장한다.
        hash_table[hash_address].append([index_key, value])
    # 2. 해쉬 충돌이 발생하지 않으면 그 공간에(key, value)를 저장
    else:
        hash_table[hash_address] = [[index_key, value]]


def read_data(data):
    index_key = get_key(data)
    hash_address = hash_function(index_key)

    if hash_table[hash_address] != 0:
        for index in range(len(hash_table[hash_address])):
            if hash_table[hash_address][index][0] == index_key:
                return hash_table[hash_address][index][1]
        return None
    else:
        return None

📍Close Hashing

# Close Hashing 기법을 적용한 hash table (리니어 기법)
hash_table = list([0 for i in range(8)])  # 해쉬 테이블 공간 생성


def get_key(data):  # 해쉬 키 생성
    return hash(data)


def hash_function(key):  # Division을 이용한 간단한 해쉬 함수
    return key % 8


def save_data(data, value):
    index_key = get_key(data)
    hash_address = hash_function(index_key)

    # 1. 해쉬 충돌이 발생할 경우 (해쉬 주소가 동일한 경우)
    if hash_table[hash_address] != 0:
        # 충돌이 일어난 주소부터 끝까지 스캔한다
        for index in range(hash_address, len(hash_table)):
            # 동일한 key일 경우 덮어쓴다
            if hash_table[index][0] == index_key:
                hash_table[index][1] = value
                return
            # 빈 공간을 찾으면 저장한다
            elif hash_table[index] == 0:
                hash_table[index] = [index_key, value]
                return
    # 2. 해쉬 충돌이 발생하지 않으면 그 공간에 데이터(key와 value)를 저장한다
    else:
        hash_table[hash_address] = [index_key, value]


def read_data(data):
    index_key = get_key(data)
    hash_address = hash_function(index_key)

    if hash_table[hash_address] != 0:
        for index in range(hash_address, len(hash_table)):
            if hash_table[index][0] == index_key:
                return hash_table[index][1]
            # 빈 공간이 나올 때까지 동일한 key를 발견하지 못하면 데이터가 없는 것
            elif hash_table[index] == 0:
                return None
    else:
        return None