What is Dijkstra's Algorithm?
- 가중치가 있는 그래프에서 하나의 시작 정점으로부터 다른 모든 정점들까지의 최단 경로를 찾는 알고리즘
- 음이 아닌 가중치를 가진 간선들로 이루어진 그래프에 적용되며 이 알고리즘의 핵심 아이디어는
Greedy 방식
작동원리
- 초기화 : 시작 정점을 제외한 모든 정점까지의 거리를 무한대로 설정하고, 시작 정점의 거리는 0으로 설정
- 방문하지 않은 정점 중 최소 거리 정점 선택 : 현재까지 발견된 가장 짧은 경로를 가진 정점을 선택
- 경로 갱신 : 선택된 정점을 경유지로 하여 다른 모든 정점까지의 경로를 검사. 새로운 경로가 더 짧은 경우, 해당 정점까지의 경로를 갱신
- 완료 검사 : 모든 정점이 방문되었으면 알고리즘을 종료. 그렇지 않다면, 2번 단계로 돌아가 반복
특징
- 다익스트라 알고리즘은 동적 프로그래밍(Dynamic Programming)의 일종으로 볼 수 있음
- 각 단계에서 현재까지 알려진 최단 경로를 저장하고, 이를 바탕으로 다음 최단 경로를 찾아냄
- 이 알고리즘은 주로 두 가지 자료 구조로 구현됨
- 배열: 간단한 구현이지만, 모든 정점을 순회하므로 시간 복잡도가 O(V^2)입니다(V는 정점의 수).
- 우선순위 큐(힙): 이 구조를 사용하면 시간 복잡도를 O((V + E) log V)로 줄일 수 있습니다(E는 간선의 수).
적용
- 네트워크 라우팅 프로토콜
- 지도 어플리케이션에서 경로 찾기
- 그래프에서 최단 경로 문제
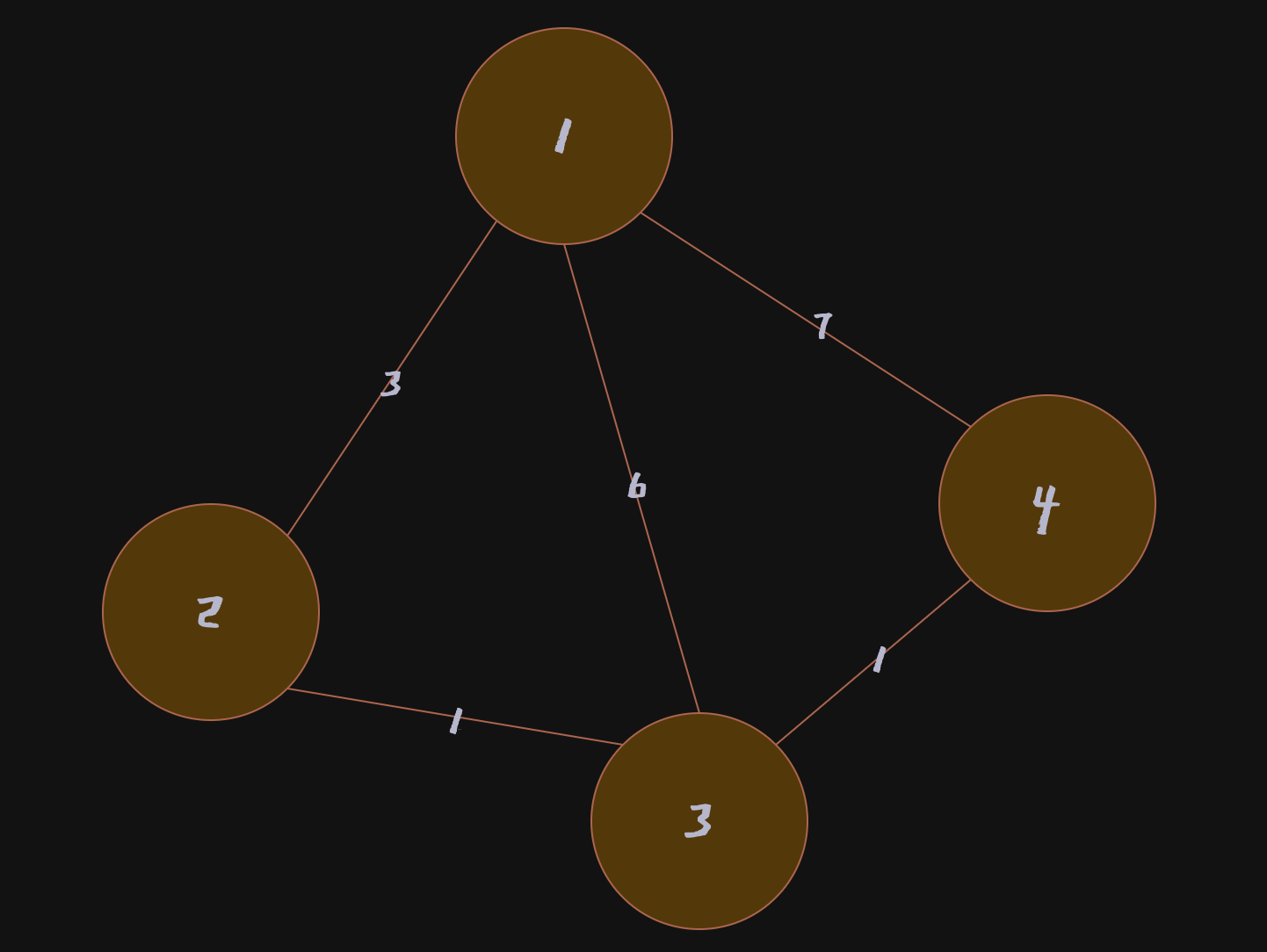
Node1부터 모든 Node까지의 최단 경로를 찾는 방법
1. 초기화 :
- 시작 노드(노드 1)의 거리 값을 0으로 설정
- 나머지 노드들의 거리 값을 무한대로 설정
- 방문 노드 집합은 비워 둠
2. 최소 거리 노드 탐색 :
- 아직 방문하지 않은 노드 중에서 거리 값이 가장 작은 노드를 선택.
처음에는 시작 노드만 거리 값이 0이므로, 노드 1을 선택
3. 인접 노드 거리 갱신 :
- 선택된 노드(노드1)에 인접한 노드들의 거리 값을 검사하고,
노드 1을 거쳐 이동하는 것이 더 짧은 경로인 경우 거리 값을 갱신
- 노드 2로의 거리는 3, 노드 4로의 거리는 7로 갱신.
노드 3은 직접 연결되어 있지 않으므로 거리 값은 변하지 않음(무한대)
4. 방문 표시
- 노드 1을 방문한 것으로 표시하고, 방문한 노드 집합에 추가함
5. 반복
- 노드 1을 제외한 나머지 노드 중에서 아직 방문하지 않고 거리 값이 가장 작은 노드를 선택함
이 경우 노드 2가 선택됨(거리값 3)
6. 인접 노드 거리 갱신(노드 2)
- 노드 2에 인접한 노드들의 거리 값을 검사. 노드 2를 거쳐 노드 3으로 가는 거리는
4(3+1)가 되고, 이는 현재 노드 3의 거리 값보다 작으므로 노드 3의 거리 값을 갱신
- 노드 2를 거쳐 노드 4로 가는 거리는 12(3+6+3)가 되지만,
이는 노드 1에서 직접 가는 거리 7보다 크므로 갱신하지 않음
7. 방문 표시(노드 2)
- 노드 2를 방문한 것으로 표시하고, 방문한 노드 집합에 추가
8. 반복
- 노드 2와 1을 제외한 나머지 노드 중에서 아직 방문하지 않고
거리 값이 가장 작은 노드를 선택함. 이경우 노드 3이 선택됨(거리값 4)
9. 인접 노드 거리 갱신(노드 3)
- 노드 3에 인접한 노드드르이 거리 값을 검사. 노드 3을 거쳐 노드 4로 가는 거리는
5(4+1)가되고, 이는 현재 노드 4의 거리 값보다 작으므로 노드 4의 거리 값을 갱신
10. 방문 표시(노드 3)
- 노드 3을 방문한 것으로 표시하고, 방문한 노드 집합에 추가
11. 반복
- 마지막으로 남은 노드 4가 방문되고, 더 이상 방문할 노드가 없으므로
알고리즘을 종료
> 노드 1 : 거리 0
노드 2 : 거리 3
노드 3 : 거리 4
노드 4 : 거리 5
다익스트라 알고리즘 예시
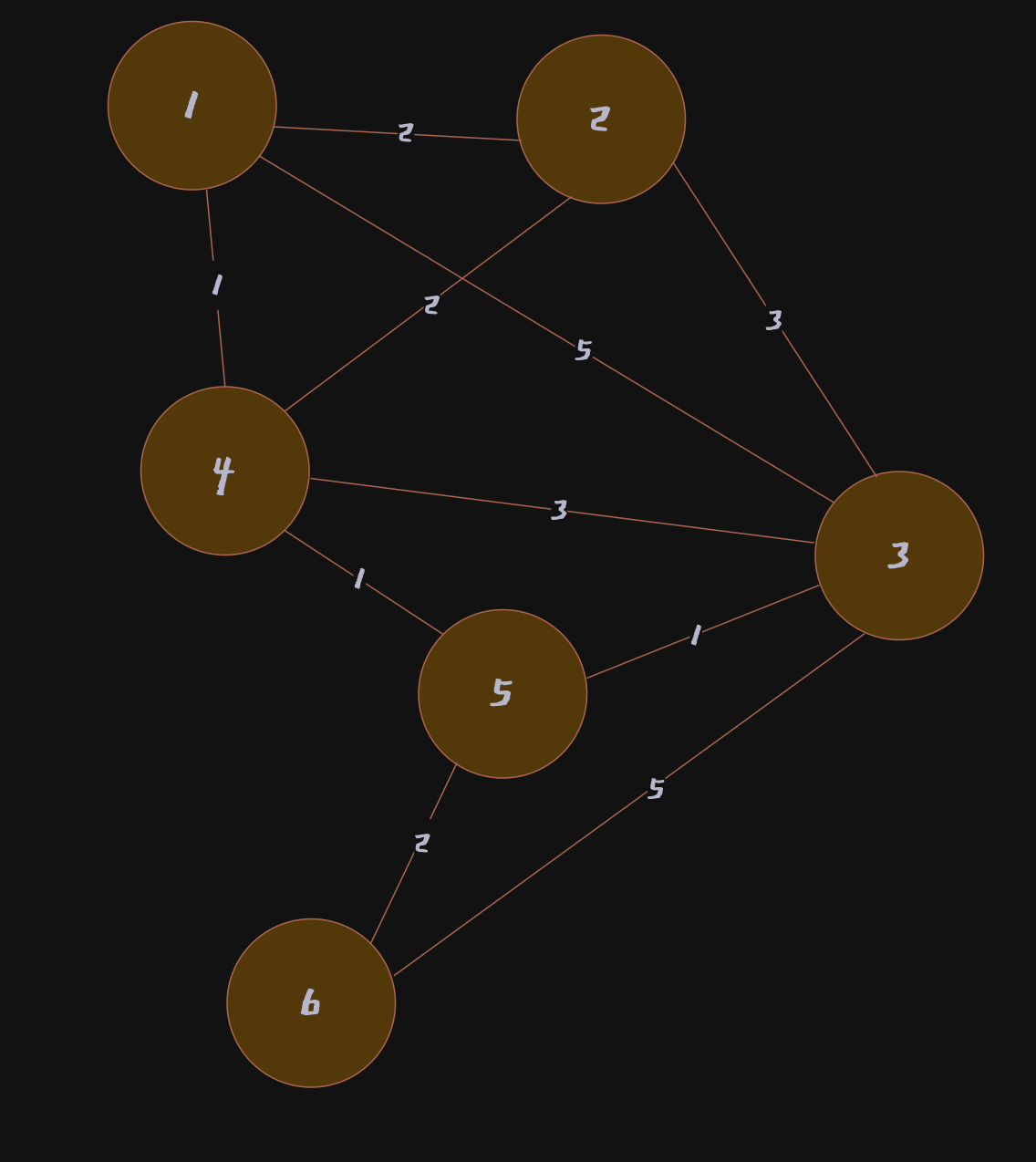
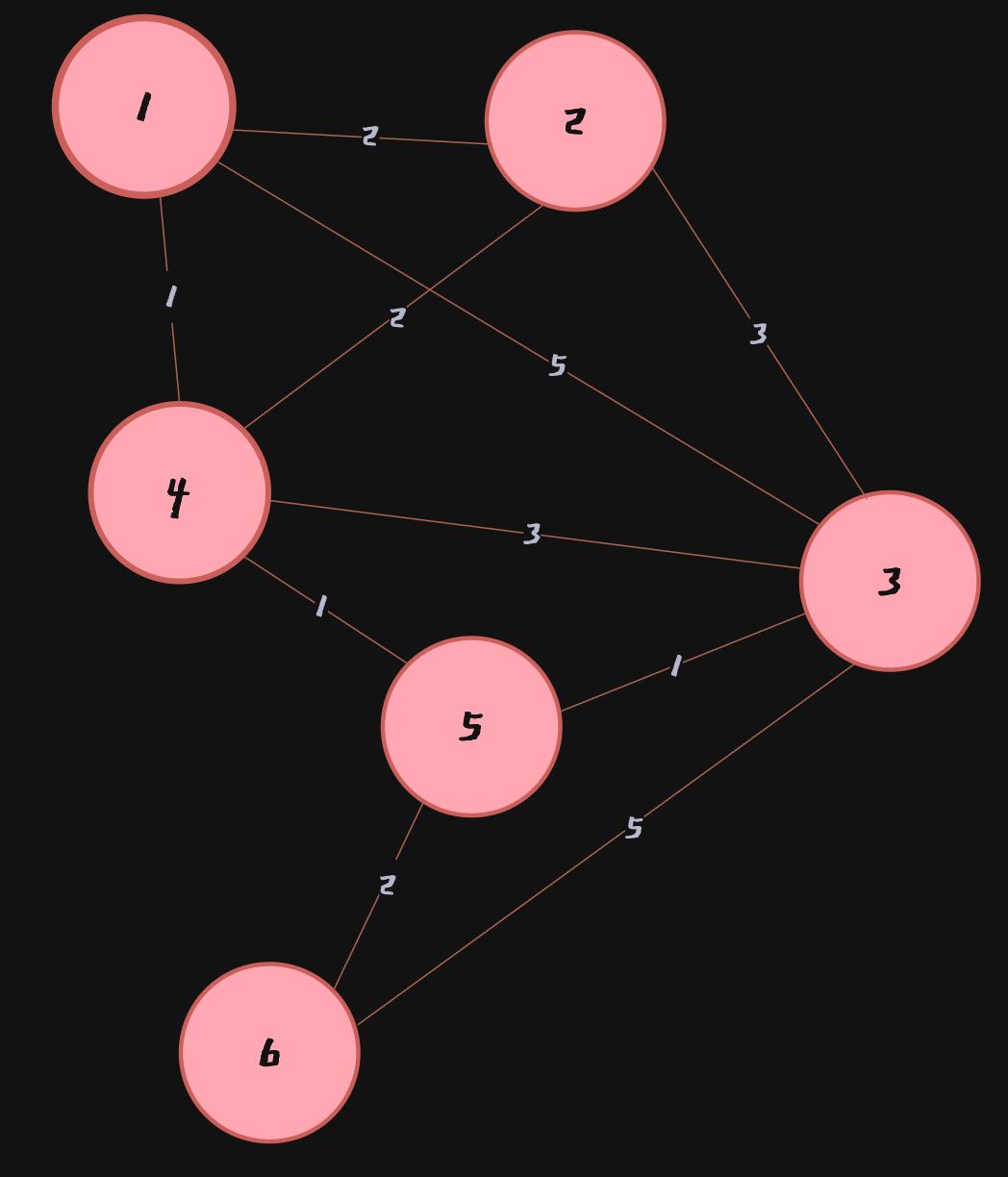
위 그림과 같은 그래프는 실제 컴퓨터 안에서 처리할 때 이차원 배열 형태로 처리해야함
아래 표의 의미는 특정 행에서 열로 가는 비용을 나타낸다.
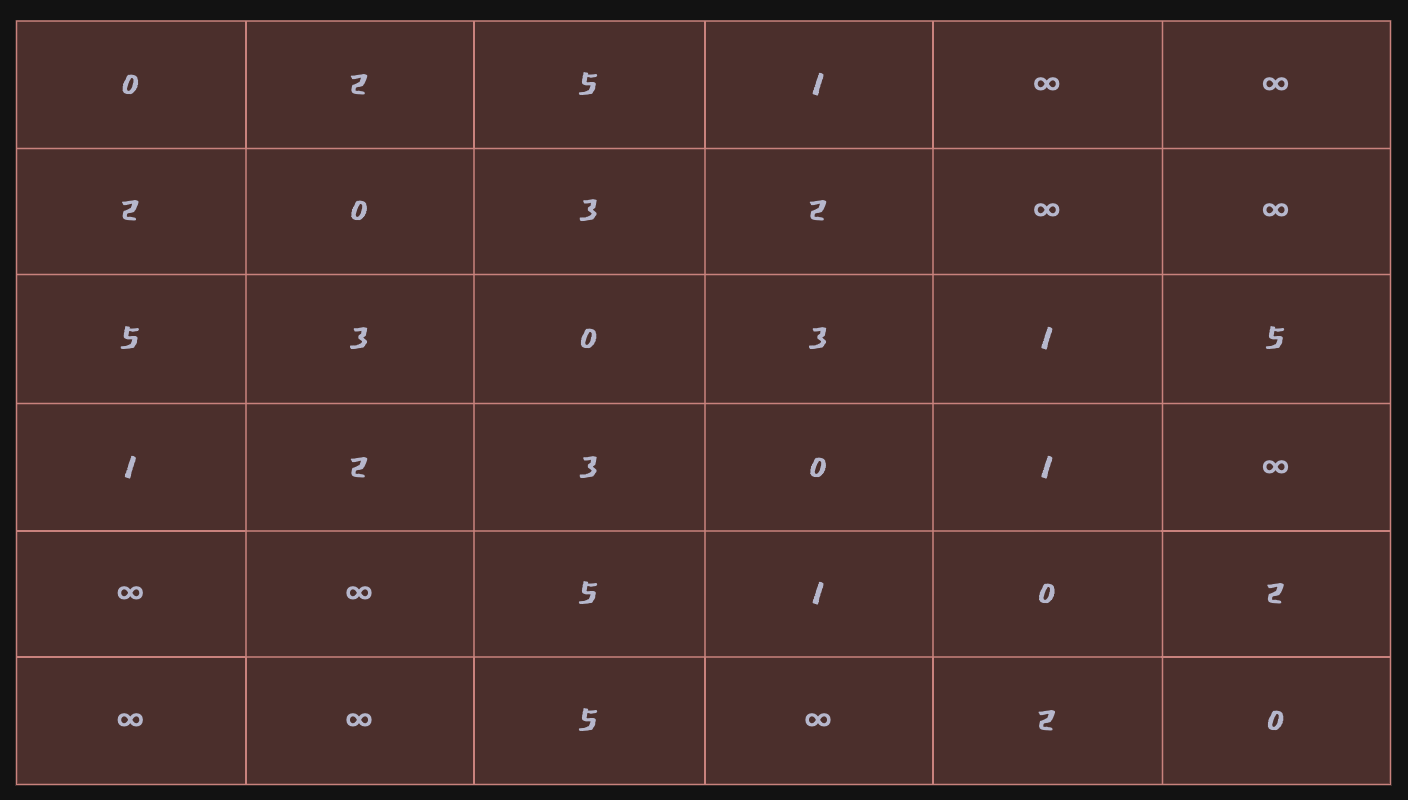
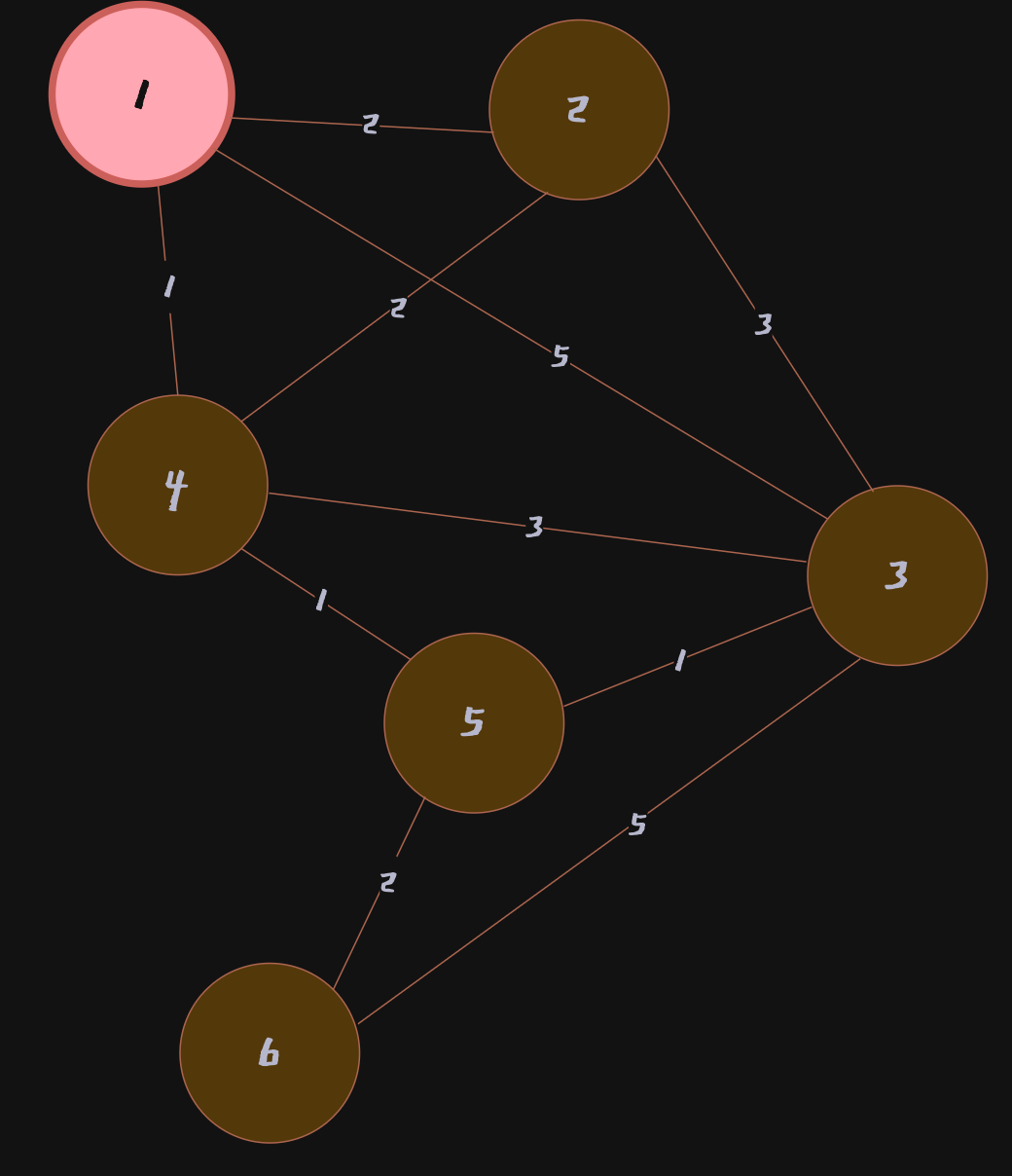
위와 같이
Node 1을 선택한 상태이고,Node 1과 연결된 세 개의 간선을 확인한 상태라고 할 수 있음. 1번 노드에서 다른 정점으로 가는 최소 비용은 다음과 같다. 배열을 만든 뒤에는 이 최소 비용 배열을 계속해서 갱신할 것이고 현재 방문하지 않은 노드 중에서 비용이 가장 적은 노드는Node 4이다.
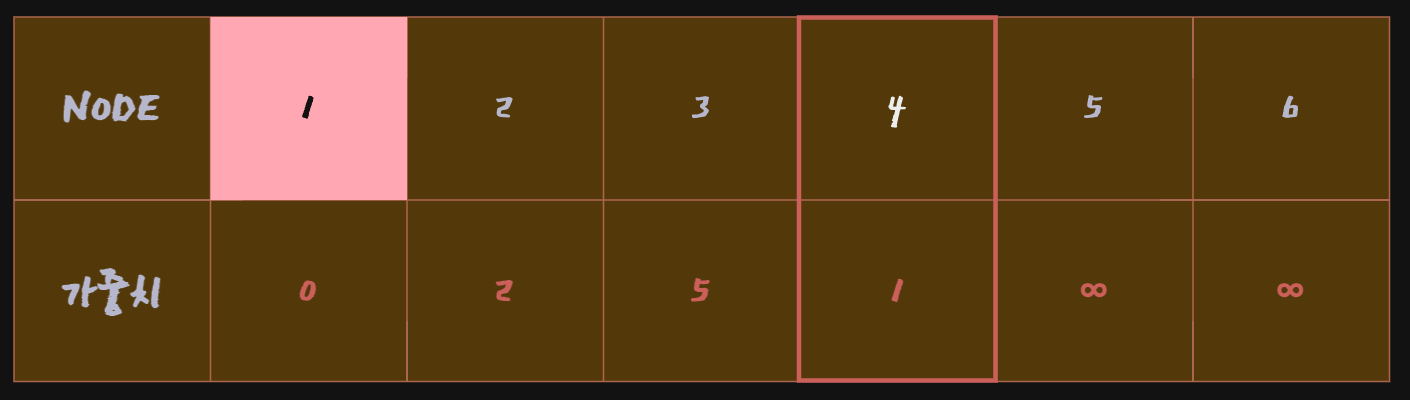
따라서 위 배열의 상태를 고려하여 Node 4가 선택됨
Node 4를 거쳐서 가는 경우를 모두 고려하여 최소 비용 배열을 갱신
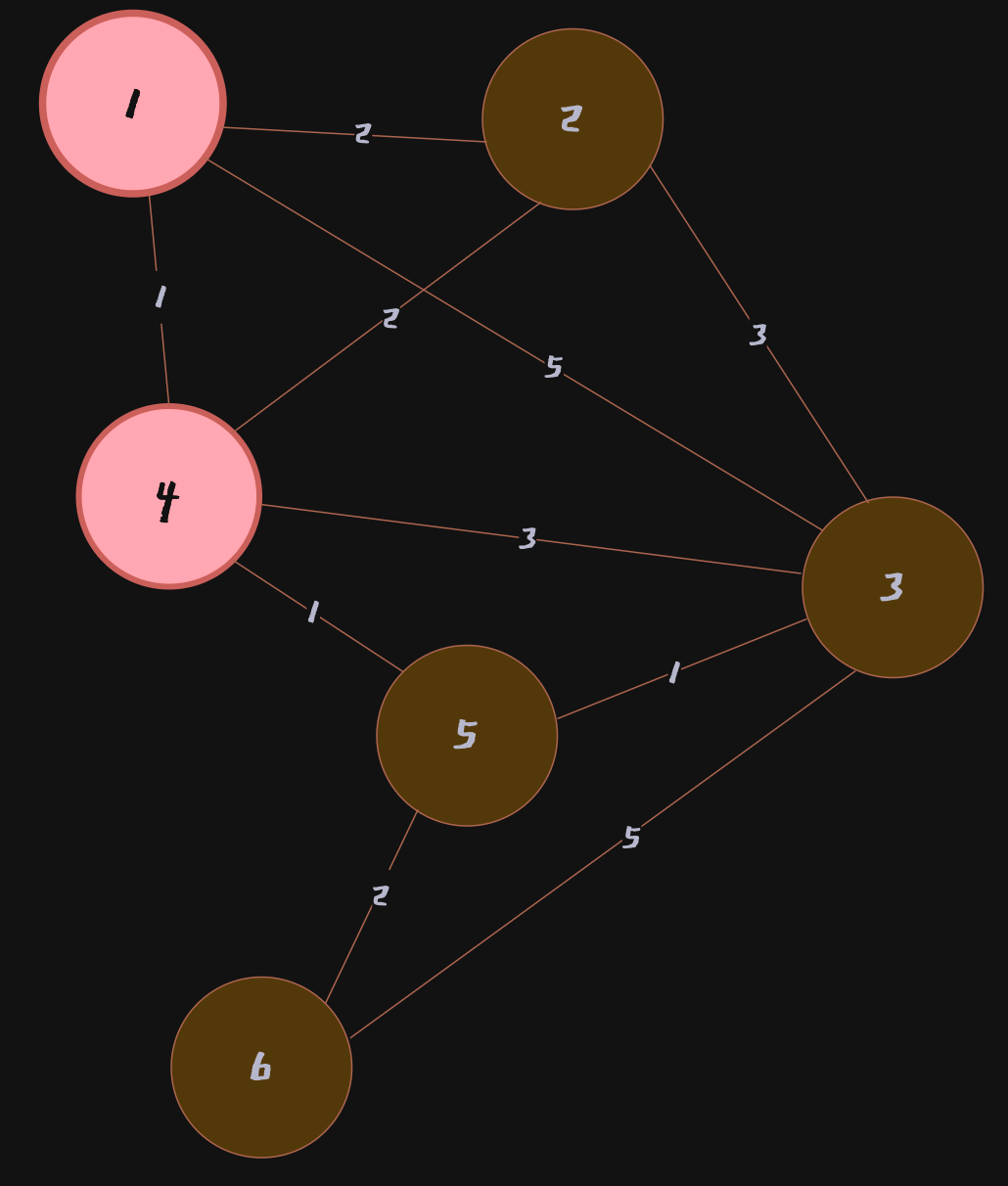
표를 보면 Node 1에서 Node 5로 바로 가는 방법이 없기 때문에 무한대였음
하지만,Node 1 → Node 4 → Node 5로 가는 경우 비용이 2이므로 최소 비용 배열을 갱신해줌
또한Node1 → Node 4 → Node 3으로 가는 경우 비용이 4이므로 기존(5)보다 저렴함
따라서 최소 비용 배열을 갱신해줌
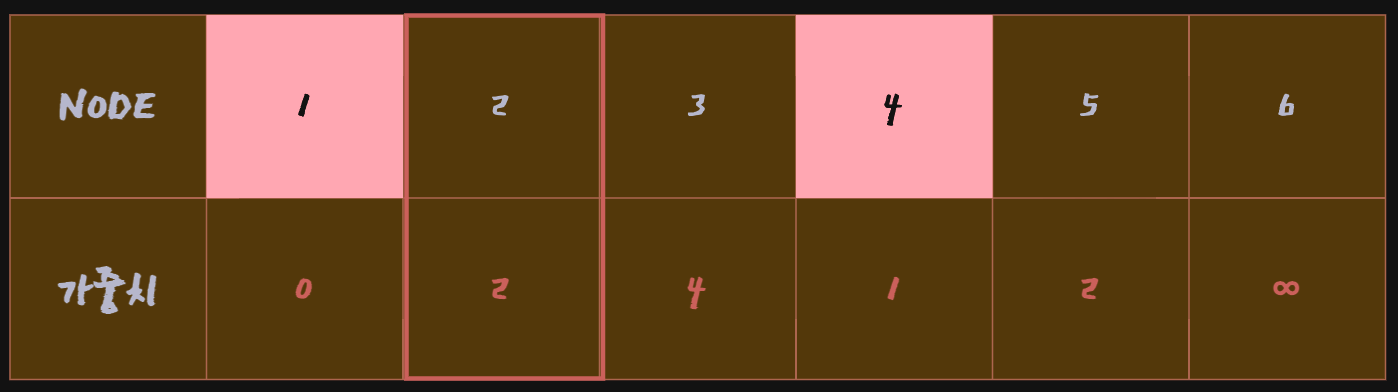
이제 다음으로 방문하지 않은 Node 중에서 비용이 가장 적은 Node 2를 선택
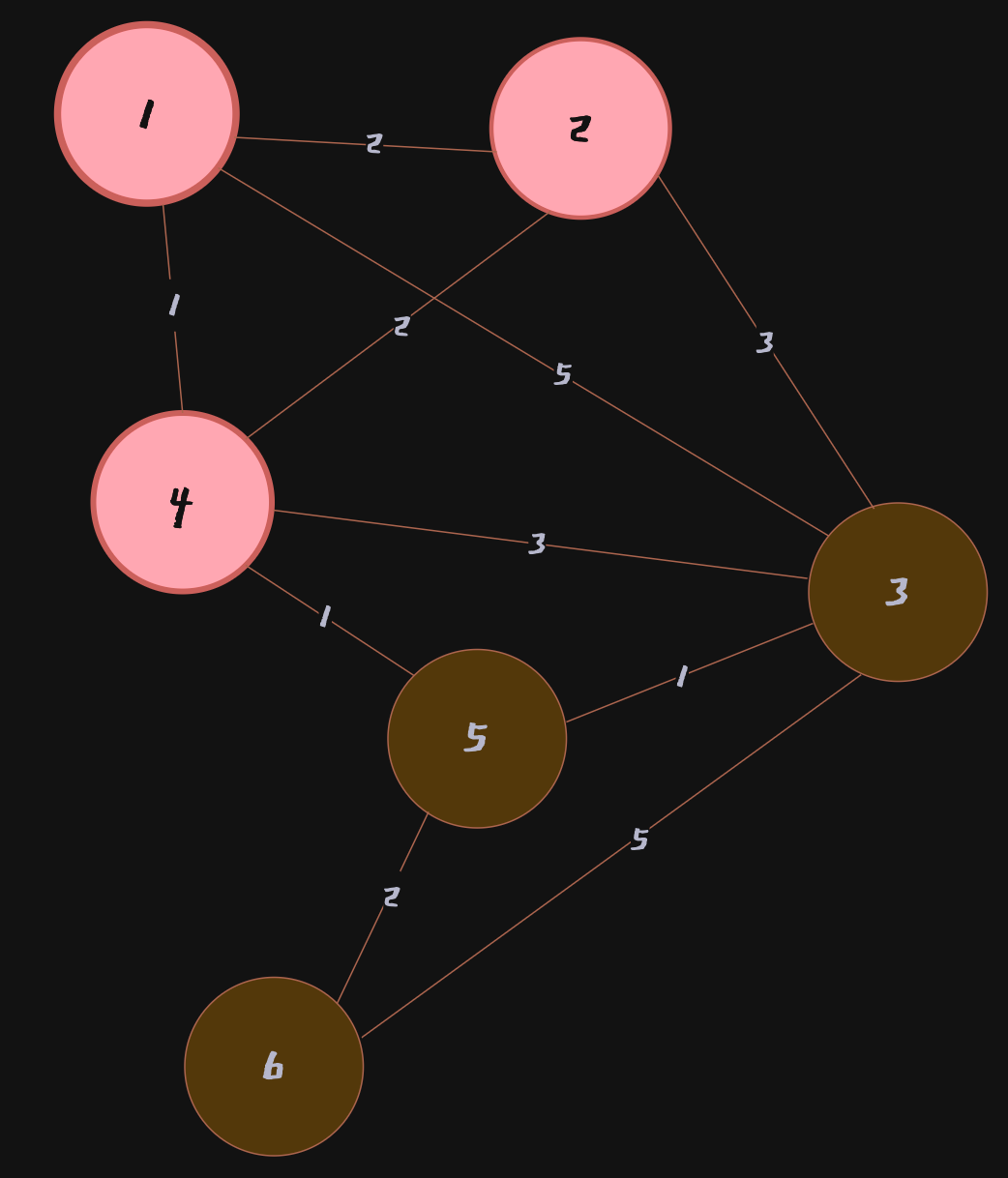
Node 2는 가더라도 비용이 갱신되는 경우가 없기때문에(
Node 1 → Node 3(5), Node 1 → Node 2 → Node 3(2+3)) 배열은 그대로 유지
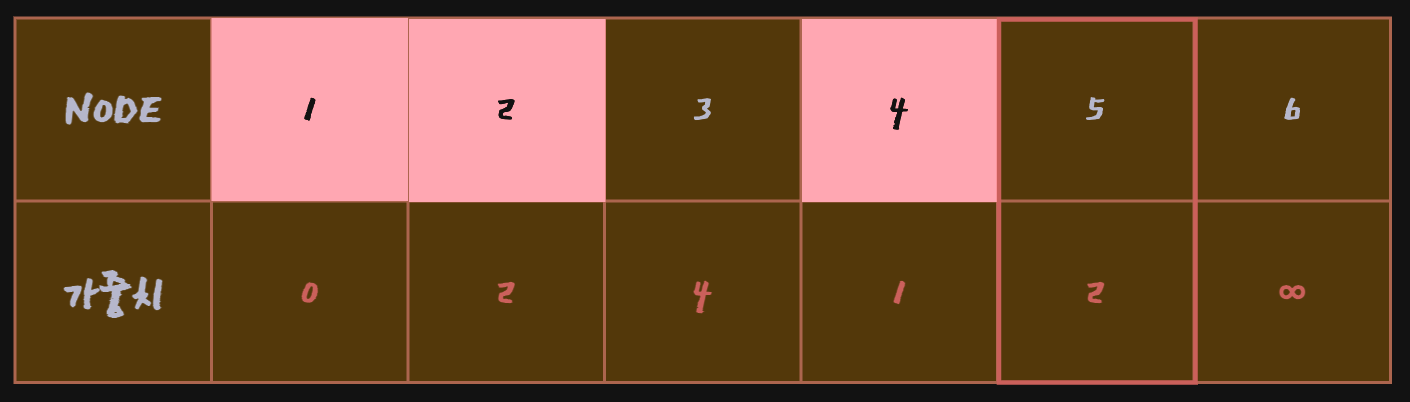
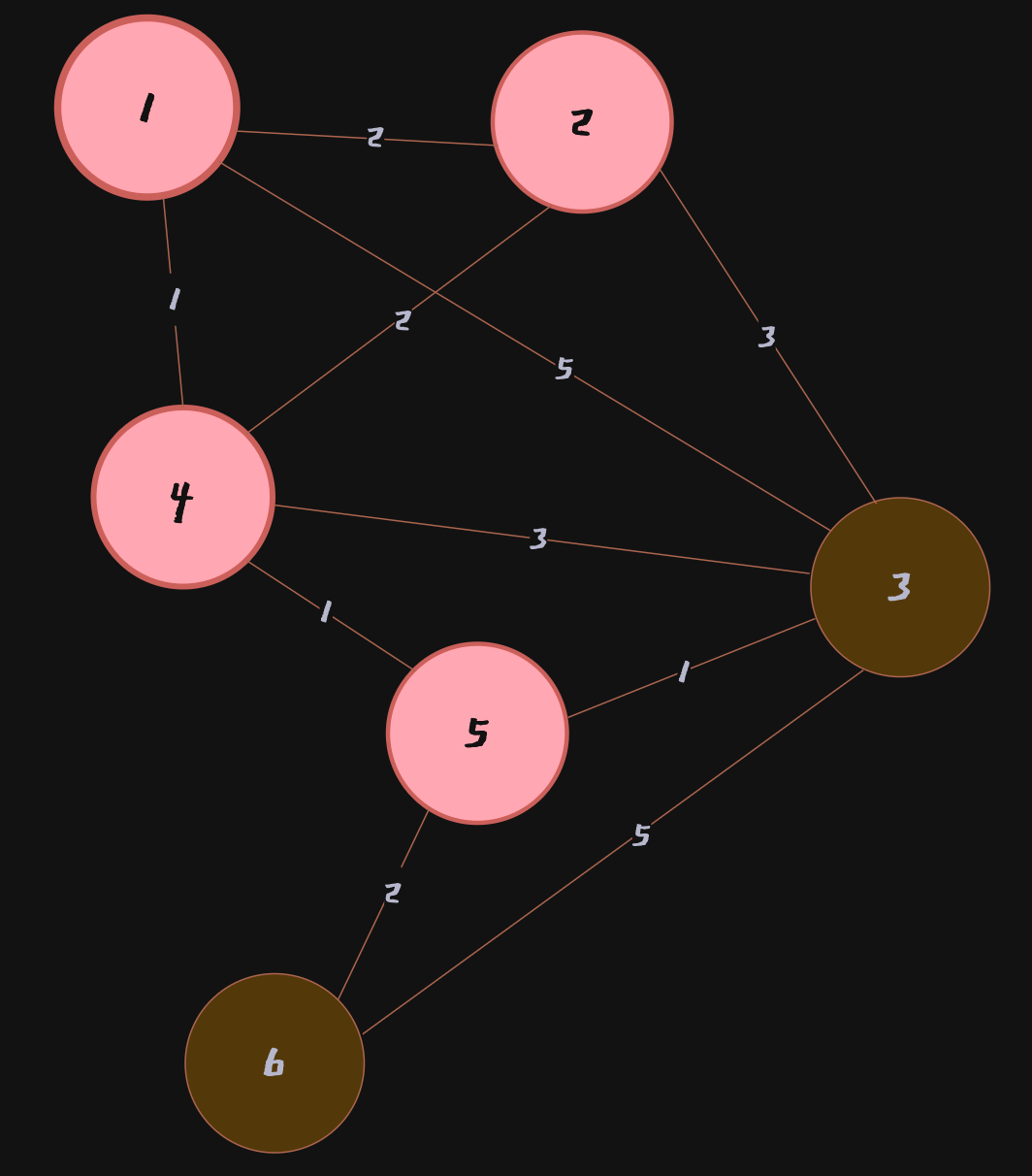
Node 1 → Node 3은 현재Node 1 → Node 4 → Node 3의 값 4로 갱신된 상태
그림과 같이Node 1 → Node 4 → Node 5 → Node 3의 값 3이 기존의 값(4) 보다 더 저렴한 비용이기때문에 갱신
또한,Node 1 → Node 6의 값 무한대에서Node 1 → Node 4 → Node 5 → Node 6의 값 4로 기존의 값(무한대) 보다 저 저렴한 비용이기때문에 갱신
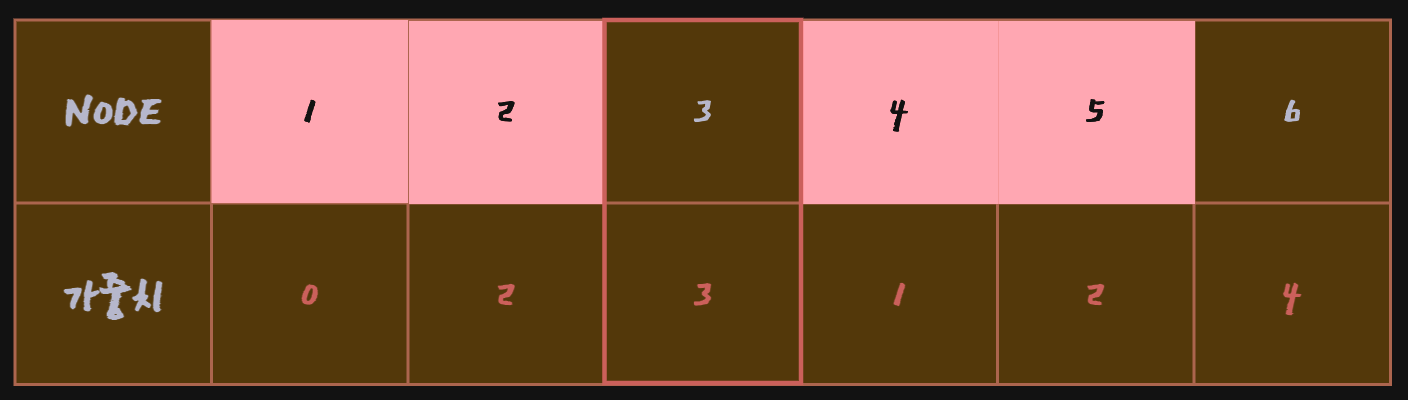
이후 방문하지 않은 노드 중에서 가장 저렴한 Node 3을 방문
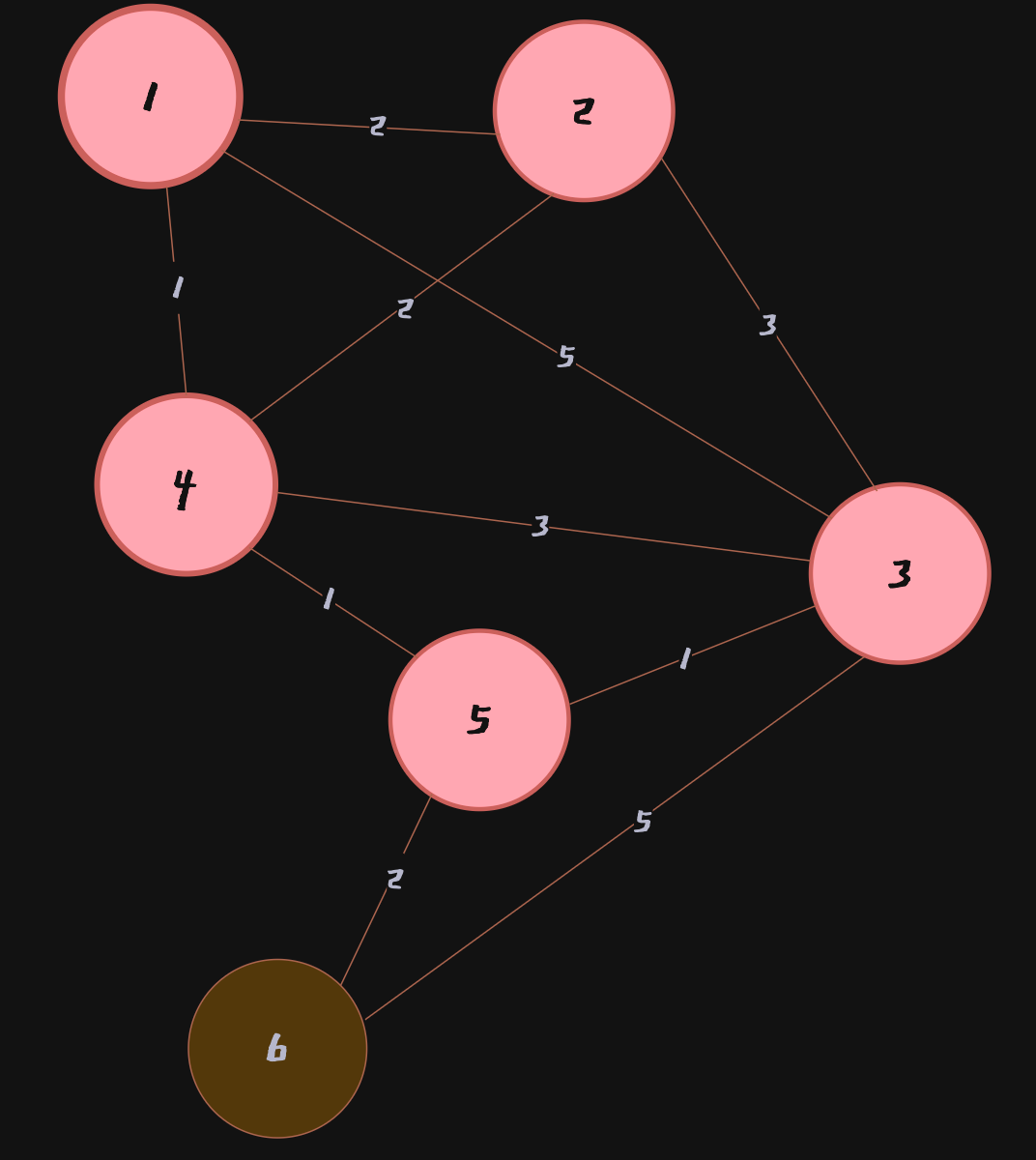
Node 1 → Node 6으로 가는 최소 비용은 현재 4,Node 1 → Node 3 → Node 6으로 가는 비용 10이기 때문에 갱신 안됨
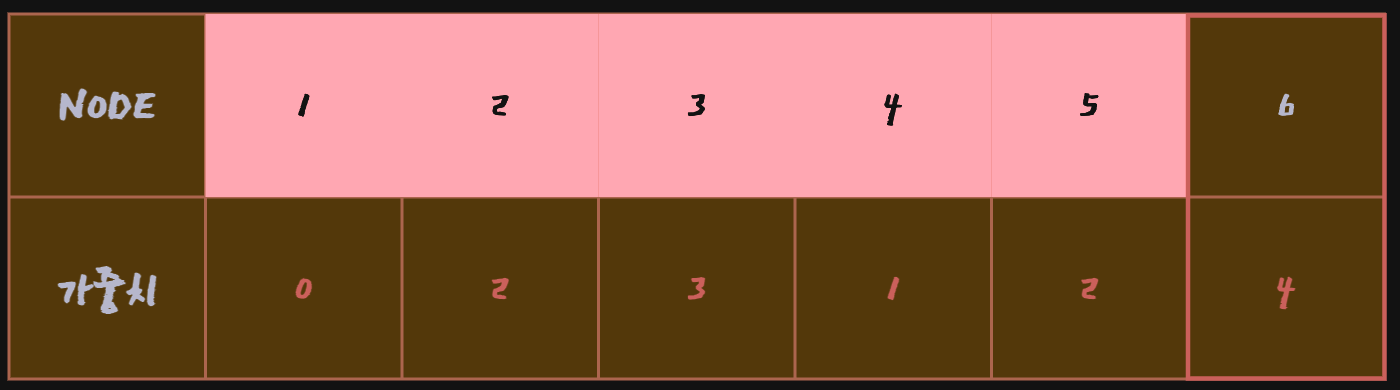
Node 6을 방문한 뒤에도 갱신된 결과가 없기때문에 최종 배열은 다음과 같음
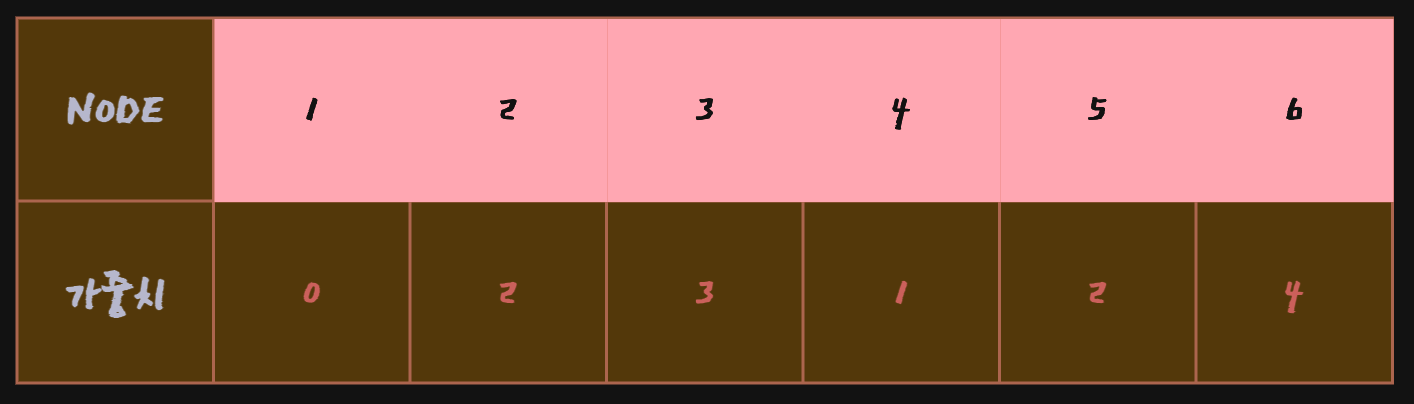
구현 로직
import java.util.*;
public class DijkstraAlgorithm {
public static final int INF = Integer.MAX_VALUE; // 무한대 값을 나타내는 상수
public static void main(String[] args) {
int n = 6; // 노드의 개수
int[][] connections = {
{1, 2, 2},
{1, 4, 1},
{2, 3, 3},
{2, 3, 5},
{3, 4, 3},
{3, 5, 1},
{4, 5, 1},
{5, 6, 2},
{6, 5, 2}
};
solution(n, connections);
}
public static void solution(int n, int[][] connections) {
// 그래프 초기화
List<List<Node>> graph = new ArrayList<>();
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<>());
}
// 간선 정보를 그래프에 저장
for (int[] conn : connections) {
int x = conn[0];
int y = conn[1];
int weight = conn[2];
graph.get(x).add(new Node(y, weight));
graph.get(y).add(new Node(x, weight));
}
// 다익스트라 알고리즘 실행
int[] distances = dijkstra(graph, 1);
// 결과 출력
for (int i = 1; i <= n; i++) {
if (distances[i] == INF) {
System.out.println("Distance from node 1 to node " + i + ": " + "Infinity");
} else {
System.out.println("Distance from node 1 to node " + i + ": " + distances[i]);
}
}
}
private static int[] dijkstra(List<List<Node>> graph, int start) {
int[] distances = new int[graph.size()];
Arrays.fill(distances, INF);
distances[start] = 0;
PriorityQueue<Node> queue = new PriorityQueue<>(Comparator.comparingInt(node -> node.weight));
queue.add(new Node(start, 0));
while (!queue.isEmpty()) {
Node currentNode = queue.poll();
if (distances[currentNode.vertex] < currentNode.weight) {
continue;
}
for (Node adjNode : graph.get(currentNode.vertex)) {
int newDist = distances[currentNode.vertex] + adjNode.weight;
if (newDist < distances[adjNode.vertex]) {
distances[adjNode.vertex] = newDist;
queue.add(new Node(adjNode.vertex, newDist));
}
}
}
return distances;
}
static class Node implements Comparable<Node> {
int vertex;
int weight;
Node(int vertex, int weight) {
this.vertex = vertex;
this.weight = weight;
}
@Override
public int compareTo(Node other) {
return Integer.compare(this.weight, other.weight);
}
}
}
