이분 탐색이란?

• 정렬된 배열에서 사용하기 적합한 탐색 방법
• 배열의 중앙값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽에 있는지 확인하는 방식
  (중앙에서 시작하기 떄문에 탐색 범위가 반으로 줄어드는 효과가 있음)
• 찾고자 하는 항목의 방향이 정해지면 반대 방향은 탐색할 필요가 없기 때문에, 매 단계마다 탐색
  범위를 반 씩 줄일 수 있음
• 이분 탐색은 이진 탐색이라고도 부름
• 탐색 시간은 O(logN)

탐색 방법

1. 정렬된 배열 array[]가 있고, 범위는 left, right로 설정
2. left, right 값으로 mid 값을 설정 : mid = (left + right) / 2
3. array[mid]의 값과 찾고자 하는 값(value)를 비교
   - value > array[mid] : left를 mid + 1로 설정
   - value < array[mid] : right를 mid - 1로 설정
   - value == array[mid] : 값을 찾았으므로 array[mid] 값 리턴
4. left가 right가 될 때까지 위 단계를 반복함

이분 탐색 예제

일반적인 탐색 방법과 이분 탐색 방법

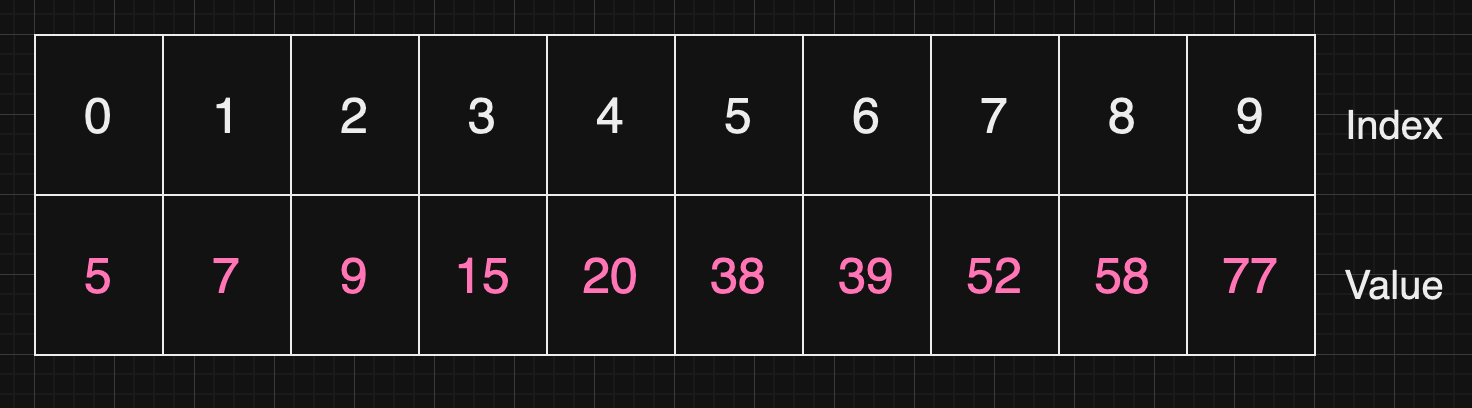
일반적인 탐색 방법

• 찾고자하는 Value : 58
• For 문을 활용하여 index 0부터 9까지 순차적으로 탐색하여 값을 찾아야 함
  • 결과적으로 8번 순차 탐색으로 찾을 수 있음

이분 탐색 방법

• 찾고자하는 Value : 58

1. 해당 배열의 중간 값을 확인 : (0 + 9 ) / 2 = 4
   index 4의 값을 확인 : 20
   58보다 작음
2. index 5부터 9까지의 범위에서 중간 값을 확인 : (5 + 9) / 2 = 7
   index 7의 값을 확인 : 52
   58보다 작음
3. index 8부터 9까지의 범위에서 중간 값을 확인 : (8 + 9) / 2 = 8
   index 8의 값을 확인 : 58
   58과 찾고자하는 Value의 값이 58 일치함을 확인

• 결과적으로 3번의 탐색으로 찾을 수 있음

구현

package programmers;

public class BinarySearch {
	
	static int[] arr;
	static int count;
	
	public static void main(String[] args) {
		
		arr = new int[] {5, 7, 9, 15, 20, 38, 39, 52, 58, 77};
		int cnt = binarySearch(58);
		System.out.println("["+ cnt+"]번만에 value값을 찾았습니다!");
	}
	
	
	public static int binarySearch(int goal) {
		int left = 0;
		int right = arr.length - 1;
		
		
		while(right >= left) {
			
			int mid = (right + left) / 2;
			count++;
			
			if(goal == arr[mid]) {
				return count;
			}else if (goal < arr[mid]) {
				right = mid - 1;
			}else {
				left = mid + 1;
			}
			
		}
		
		return -1;
	}

}