비트(Binary Digit)

• 비트는 컴퓨터에서 데이터를 나타내는 가장 작은 단위이다. 이는 0 또는 1 두 가지 상태만을 나타낼 수 있는 이진수이다. Java에서 부호 없는 N비트 정수형 변수는 최대 N개의 이진수 자리를 사용해 데이터를 표현할 수 있으며, 각 비트의 가치는 2^0부터 2^(N-1)까지의 값을 가질 수 있다.

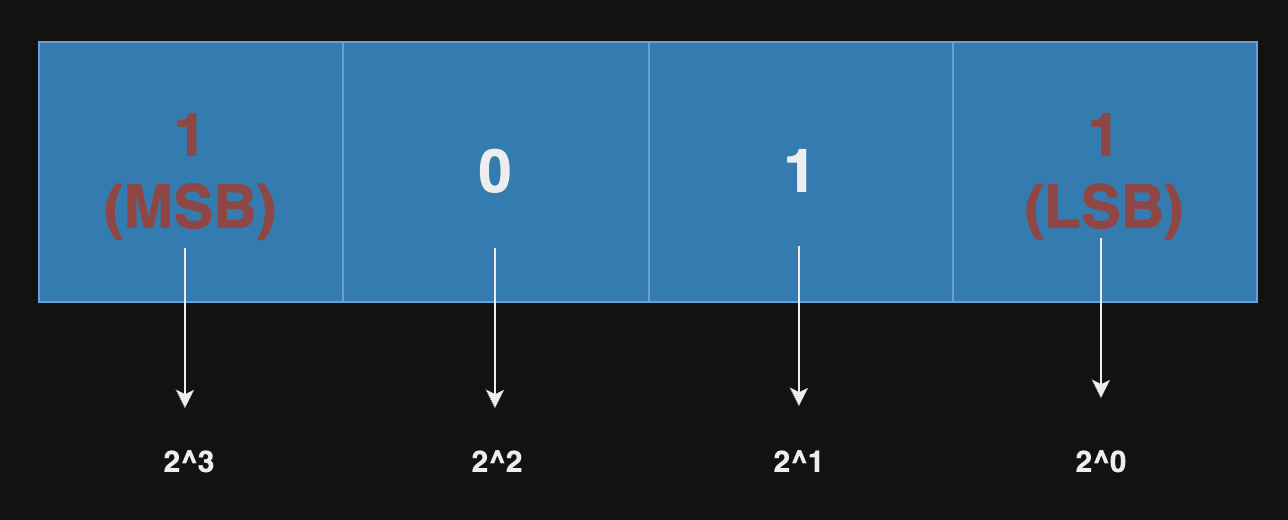
• 최상위 비트(MSB, Most Significant Bit)는 2^(N-1)을 나타내며 최하위 비트(LSB, Least Significant Bit)는 2^0을 나타낸다.

4bit 정수형의 예시(10진수 11)

• 이진수의 각 자리는 2의 거듭제곱 값을 나타낸다.

비트 연산자(Java)

구분	연산자	의미	설명
비트연산자	&	AND	두 정수의 각 비트를 비교하여 둘 다 1이면 결과도 1, 아니면 0을 반환
비트연산자	⎮	OR	두 정수의 각 비트를 비교하여 하나라도 1이면 결과가 1, 아니면 0을 반환
비트연산자	^	XOR	두 정수의 각 비트를 비교하여 서로 다르면 1, 같으면 0을 반환
비트연산자	~	NOT	정수의 각 비트를 1이면 0, 0이면 1로 바꾸는 연산
비트이동자	<<	Left Shift	정수를 왼쪽으로 지정된 비트 수만큼 이동시키며, 빈자리는 0으로 채운다
비트이동자	>>	Right Shift	정수를 오른쪽으로 지정된 비트 수만큼 이동시키며, 빈 자리는 정수의 MSB와 같은 값으로 채운다
비트이동자	>>>	Unsigned Right Shift	정수를 오른쪽으로 지정된 비트 수 만큼 이동시키며, 빈자리는 0으로 채운다

---

예제

public class BitTest {
	
	public static void main(String[] args) {
		
		int x = 10;
		int y = 12;
		
		System.out.println("x= " + Integer.toBinaryString(x));
		System.out.println("y= " + Integer.toBinaryString(y));
		System.out.println("x|y= " + Integer.toBinaryString(x|y));
		System.out.println("x&y= " + Integer.toBinaryString(x&y));
		System.out.println("x^y= " + Integer.toBinaryString(x^y));
		System.out.println("~x= " + Integer.toBinaryString(~x));
	}

}

비트마스크(BitMask)

• 비트마스크는 이진수를 이용한 연산으로 연산이 빠르고 메모리 효율성이 높은 장점이 있다. 각 비트는 켜짐 혹은 꺼짐의 상태를 나타내며 이를 통해 집합의 표현 및 연산을 할 수 있다.

비트마스크의 장점

• 연산 속도가 빠르며 대부분 O(1)에 구현된다.
• 비트 연산자를 사용하여 코드가 간결해진다.
• 메모리를 절약할 수 있으며, 다수의 데이터를 미리 계산하여 저장하는 데 유용하다.

비트마스크를 이용한 집합 구현

• 비트마스크를 이용한 집합 구현은 가장 대표적이고 자주 쓰이는 방법이다. 하나의 bit가 하나의 데이터 상태를 의미한다. bit가 1이면 해당 원소가 집합에 포함되어 있다는 의미이고, 0이면 포함되어 있지 않다는 의미이다. 따라서, N개의 원소를 갖는 집합의 부분 집합들을 모두 표현할 수 있다.

연산	코드	설명	예시
공집합	A = 0;	모든 원소가 포함되지 않은 집합을 의미한다.	int A = 0;
전체 집합	A = (1 << N) - 1;	가능한 모든 원소가 포함된 집합을 의미한다. N은 집합에 포함할 수 있는 원소의 총 개수이다.	int A = (1 << 4) - 1; // 15, 즉 1111
원소 추가	A ⎮= (1 << k);	집합 A에 k번째 원소를 추가한다.	A ⎮= (1 << 2); // 2번째 원소를 추가
원소 삭제	A &= ~(1 << k);	집합 A에서 k번째 원소를 제거한다.	A &= ~(1 << 2); // 2번째 원소를 제거
원소 확인	(A & (1 << k)) == (1 << k);	집합 A에 k번째 원소가 포함되어 있는지 확인한다.	if((A & (1 << 2)) == (1 << 2)) { /* 2번째 원소가 포함되어 있음 */ }
원소 토글	A ^= (1 << k);	집합 A의 k번째 원소가 포함되어 있다면 제거하고, 포함되어 있지 않다면 추가한다.	A ^= (1 << 2); // 2번째 원소 토글
합집합	A ⎮ B;	두 집합 A와 B의 합집합을 구한다.	int union = A ⎮ B;
교집합	A & B;	두 집합 A와 B의 교집합을 구한다.	int intersection = A & B;
차집합	A & (~B);	집합 A에서 집합 B에 포함된 원소를 제외한 집합을 구한다.	int difference = A & (~B);
대칭차집합	A ^ B;	두 집합 A와 B 중 한 집합에만 포함된 원소들의 집합을 구한다.	int symmetricDifference = A ^ B;
집합 크기	Integer.bitCount(A);	집합 A에 포함된 원소의 개수를 구한다.	int size = Integer.bitCount(A);
최소 원소 찾기	A & (-A);	집합 A에서 가장 작은 원소를 찾는다.	int smallest = A & (-A);
최소 원소 지우기	A &= (A - 1);	집합 A에서 가장 작은 원소를 제거한다.	A &= (A - 1);
부분 집합 순회	for (int subset = A; subset > 0; subset = (subset - 1) & A) {}	집합 A의 모든 부분 집합을 순회한다.	for (int subset = A; subset > 0; subset = (subset - 1) & A) { /* 부분 집합 처리 */ }

공집합

• 모든 원소가 포함되지 않은 상태를 나타내므로 모든 비트가 꺼져 있는 상태인 0으로 표현된다.

꽉 찬 집합(전체 집합)

• 꽉 찬 집합은 가능한 모든 원소가 포함된 상태를 나타내므로, 모든 비트가 켜져 있는 상태를 나타내며 예를들어 4개의 원소를 나타내는 전체 집합의 경우 1111(2진수) 15(10진수)가 된다.

원소 추가

• 집합 A에 새로운 원소 k를 추가하려면 k번째 위치의 비트를 1로 설정해야한다. 이를 위해 OR 연산(⎮)을 사용하여 해당 비트만을 1로 만들 수 있다. 예를들어, 집합 A에 2번째 원소를 추가하고자 할때, A ⎮= (1 <<2) 연산을 사용한다.

원소 삭제

• 집합 A에서 원소 k를 제거하려면 k번째 위치의 비트를 0으로 설정해야 한다. 이를 위해 AND 연산(&)과 NOT(~)을 결합하여 사용한다. 예를들어, A &= ~(1<<2)연산은 집합 A에서 2번째 원소를 삭제한다.

원소의 포함 여부 확인

• 집합 A에서 원소 k가 포함되어 있는지 확인하려면 AND 연산을 사용하여 해당 비트 위치가 1인지 확인한다. if((A & (1<<k) == (1<<k))구문은 원소 k가 집합A에 포함되어 있는지 검사한다.

원소의 토글

• 집합 A에서 원소 k의 상태를 토글하려면 XOR(^)을 사용한다. 이 연산은 원소가 집합에 있을 경우 제거하고, 없을 경우 추가한다. 예를들어 A ^= (1<<k)연산은 원소 k의 포함 상태를 토글한다.

두 집합에 대해 연산하기

• 두 집합 A와 B에 대해 합집합, 교집합, 차집합을 구할 때 비트 연산자를 사용한다. 합집합은 OR 연산(⎮), 교집합은 AND(&), 차집합은 AND와 NOT 연산을 조합한 A &(~B)를 사용한다.

집합의 크기 구하기

• 집합 A의 크기 즉, 포함된 원소의 개수를 구하려면 켜져 있는 비트의 수를 세면된다. Java에서는 Integer.bitCount(A) 메서드를 사용하여 이를 쉽게 계산할 수 있다.

최소 원소 찾기

• 집합 A에 포함된 가장 작은 원소 즉, 가장 오른쪽에 있는 1비트를 찾으려면, A와 -A의 AND 연산을 수행한다. -A는 A의 2의 보수이므로 A & (-A) 연산은 가장 오른쪽의 1비트를 찾아준다.

A = 1010
---------
~A = 0101
+1
---------
-A = 0110

따라서 

 1010(A)
&0110(-A)
----------
 0010

최소 원소 지우기

• 집합 A에서 가장 작은 원소를 제거하려면 A &= (A-1)연산을 사용한다. 이 연산은 가장 오른쪽 1비트를 0으로 바꾸고, 그 보다 오른쪽에 있는 모든 비트를 1로 바꾼다.

A = 1010
---------
A-1 = 1001
---------
A&(A-1) = 1000

모든 부분 집합 순회하기

A : 1010
1) 1010 > subset - 1 : 1001 & A : 1000
2) 1000 > subset - 1 : 0111 & A : 0010
3) 0010 > subset - 1 : 0001 & A : 0000