선택 정렬 (Selection Sort)

1. 작동 방식

선택 정렬은 정렬 알고리즘 중 하나로, 배열을 순회하여 가장 작은 원소를 찾은 후, 맨 앞의 원소와 그 원소를 바꾸는 식으로 동작한다.

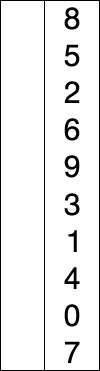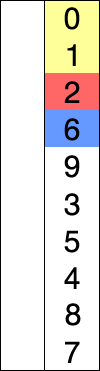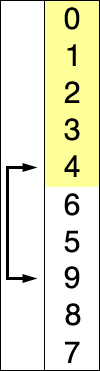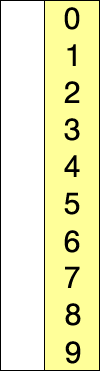
출처 : https://en.wikipedia.org/wiki/Selection_sort

위의 그림처럼 선택 정렬 시 정렬된 원소의 부분 집합과 아직 정렬되지 않은 원소의 부분 집합으로 나뉜다. 정렬되지 않은 원소의 부분 집합에서 가장 작은 원소를 찾아 그 부분 집합의 맨 앞의 원소와 위치를 바꾼다. 그 후에 정렬된 원소의 부분 집합의 오른쪽 경계를 한 칸 늘린다. 이 일련의 동작을 전체 원소가 정렬될 때까지 반복한다.

2. 구현

// 구현부
void SelectionSort(int* arr, int size)
{
	// 정렬된 부분 집합의 오른쪽 경계 하나씩 늘리기
	for (int i = 0; i < size - 1; ++i)
	{
    	// 정렬되지 않은 부분 집합에서 가장 작은 원소 찾기
		int min_idx = i;
		for (int j = i + 1; j < size; ++j)
		{
			if (arr[j] < arr[min_idx])
			{
				min_idx = j;
			}
		}
        
		// 찾은 원소와 정렬되지 않은 부분 집합의 맨 앞 원소 바꾸기
        // (두 원소가 같지 않을 경우)
        if (i != min_idx)
        {
        	std::swap(arr[i], arr[min_idx]);
        }
	}
}

// 실행부
int main()
{
	int arr[]{ 5, 4, 3, 2, 1 };
    int size = sizeof(arr) / sizeof(arr[0]);
    
    SelectionSort(arr, size);
    for (const auto& ele : arr)
    {
    	std::cout << ele << " ";
    }
    
    // 출력 : 1 2 3 4 5
}

3. 시간 복잡도 / 공간 복잡도

- 시간 복잡도

최선, 평균, 최악 : $O(n^2)$

가장 작은 원소를 찾기 위해 필요한 연산의 수가 $(n - 1) + (n - 2) + ... + 1 = n(n - 1) / 2$ 이므로 시간 복잡도는 $O(n^2)$이다.

- 공간 복잡도

선택 정렬은 여분의 메모리 공간을 필요로 하지 않고 배열 내에서 원소의 교환이 이루어지기 때문에 공간 복잡도는 $O(1)$이다.

4. 장점 / 단점

- 장점

1. 원리가 단순하며 구현이 쉽다.
2. 주어진 데이터의 크기가 작을 때 다른 정렬 알고리즘과 성능의 차이가 크지 않다.
3. 메모리의 제약이 있을 경우 사용이 가능하다.

- 단점

1. 불안정 정렬이기 때문에, 데이터의 순서를 보장할 수 없다.
2. 주어진 데이터의 크기가 클 경우 다른 정렬 알고리즘에 비해 비효율적이다.
3. 최선의 상황에서도 시간 복잡도가 $O(n^2)$이기 때문에, 이미 정렬되어 있는 경우 비효율적이다.