문제 설명
이번 포스팅은 백준 1967번: 트리의 지름 문제 풀이에 대한 기록입니다.

[ 입출력 ]
문제를 간단히 요약하자면, "트리에서 가장 거리가 먼 두 노드 간의 거리, 즉 트리의 지름을 알아내는 문제" 입니다.
풀이
1. 처음 생각했던 풀이
처음 이 문제에 도전했을 때, 머리를 짜내어 어떻게든 채점에 통과하기는 했었습니다!
(아래가 그 코드이지만 좋은 코드는 아니니 굳이 읽어보진 않으셔도 됩니다..ㅎㅎ)
import sys
from itertools import combinations
from collections import deque
input = sys.stdin.readline
n = int(input())
from_root = [0]*(n+1)
parents = [0]*(n+1)
tree = [[] for _ in range(n+1)]
# 입력 받기
p = 0
for _ in range(n-1):
p, c, w = map(int, input().split())
tree[p].append((c, w))
# root부터 탐색하며 모든 노드에 대해 root와의 거리 측정
q = deque([1])
while q:
curr = q.popleft()
for c, w in tree[curr]:
if parents[c] == 0:
parents[c] = curr
from_root[c] = from_root[curr] + w
q.append(c)
# 리프 노드만을 모은 list 생성 (리프가 지름의 양 끝점이 되기 때문)
# root의 자식이 하나라면 root도 지름의 양 끝점 중 하나가 될 수 있으므로 포함
leaves = [i for i in range(p+1, n+1)]
if len(tree[1]) > 0 and len(tree[1]) < 2:
leaves.append(1)
# 두 리프 노드의 최소공통조상(LCA)을 구하고
# 미리 계산했던 각 노드와 root와의 거리를 이용하여 두 노드 간의 거리를 계산
# 모든 조합에 대해 위 과정을 반복하여 최대 거리를 도출
max = 0
for case in combinations(leaves, 2):
p1 = []
lca = case[0]
while lca > 1:
p1.append(parents[lca])
lca = parents[lca]
lca = case[1]
while lca not in p1:
lca = parents[lca]
dist = from_root[case[0]] + from_root[case[1]] - 2*from_root[lca]
if max < dist:
max = dist
print(max)
그리고 이게 채점 결과입니다.
보시다시피 굉장한 메모리와 시간을 잡아먹고 있고, 상대적으로 빠른 PyPy3로 채점을 돌려야만 통과했습니다.
이걸 보고 이 문제를 풀었다고하고 넘어갈 수 없었습니다!
분명 더 빠르고 멋있는 풀이가 있을 것이라 생각하고 공부해봤더니, 역시나 제가 모르고 있던 신기한 개념이 있었습니다.
2. 트리의 지름을 구하는 방법 (+증명)
의 시간으로 트리의 지름을 구하는 공식과도 같은 방법이 있었습니다.
바로 "임의의 정점 x에서 가장 먼 정점 y를 구하고, y로부터 가장 먼 정점 z를 구하면 y, z 사이의 거리가 트리의 지름" 이라는 것입니다!
처음에 저 방법을 접했을 땐,
뭔가 '오 뭔가 그럴 것 같아..!' 라는 느낌은 들었지만,
완벽히 이해되고 와닿지 않았기 때문에, 이를 증명하는 과정을 알아봤습니다.
[ 증명 ]
만약 임의의 정점 x에서 가장 먼 정점 y가 지름의 양쪽 끝점 중 하나라면, y로부터 가장 먼 정점 z는 자연스럽게 지름의 반대쪽 끝점이 되고 (지름의 양 끝점은 당연히 서로 가장 멀리 떨어진 점이기 때문), 자연스레 y와 z 사이의 거리가 트리의 지름이 됩니다.
따라서, "임의의 정점 x로부터 가장 먼 정점 y가 항상 지름의 양쪽 끝점 중 하나인가" 를 증명하면 위 방법이 올바르다는 것을 증명할 수 있습니다.
차근차근 증명하는 과정을 살펴보겠습니다.
어떤 트리에서 정점 , 를 연결하는 경로가 이 트리의 지름이라고 먼저 가정을 하고 시작합니다.
이때 임의의 정점 로부터 가장 먼 노드 를 구한다면, 가능한 경우의 수는 아래와 같이 나눠볼 수 있습니다.
1. 가 또는 인 경우
2. 가 또는 인 경우
3. , , , 와 모두 서로 다른 경우
1번의 경우 : 가 또는 인 경우, 에서 가장 먼 노드 는 지름의 양 끝점 중 하나인 또는 가 됨 O
2번의 경우 : 가 지름의 양 끝점 중 하나인 또는 임 O
3번의 경우가 조금 복잡합니다.
3번 경우는 또 다시 두 가지 케이스로 나눌 수 있습니다.
3-1. - 간의 경로가 - 간의 경로와 한 정점 이상 공유
3-2. - 간의 경로가 - 간의 경로와 완전히 독립적
3-1번의 경우.
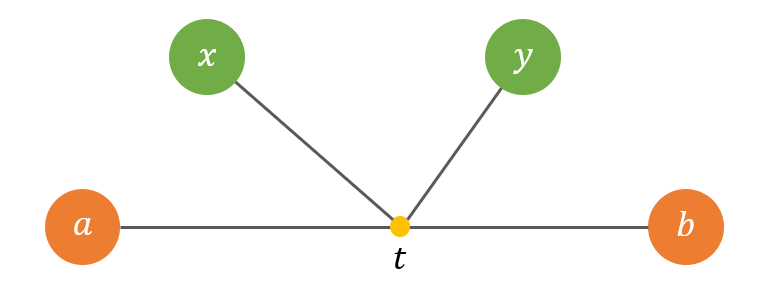
두 정점의 거리를 로 표현하면, 위 그림에서는 = + 입니다.
우리는 와 가장 먼 정점을 라고 했습니다.
따라서 는 에서 가장 먼 정점과의 거리가 되어야, "가 에서 가장 먼 정점" 이라는 것이 성립합니다. 즉, "는 에서 가장 멀리 떨어진 점" 이어야 합니다.
는 트리의 지름 위의 정점입니다. 따라서 와 가장 먼 정점은 또는 입니다.
- 는 에서 가장 멀리 떨어진 정점이어야 함
- 와 가장 먼 정점은 또는
따라서 는 또는 가 됩니다. 이는 "임의의 정점 x으로부터 가장 먼 정점 y가 항상 지름의 양쪽 끝점 중 하나인가" 에 성립하므로 O
3-2번의 경우.
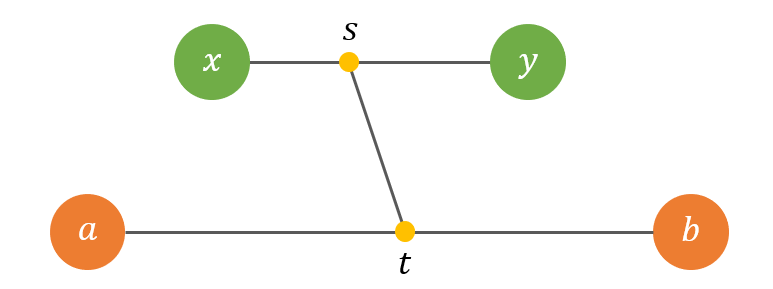
위 그림에서 - - 간의 거리는 각각
= +
= + 입니다.
3-1에서와 마찬가지로 가정에 의해서, 아래와 같이 정리할 수 있습니다.
- 는 에서 가장 멀리 떨어진 점이어야 함
- 는 에서 가장 멀리 떨어진 점이어야 함
그러나, 위 두 가지는 양립할 수 없습니다.
먼저 "는 에서 가장 멀리 떨어진 점이어야 함"이 성립한다면,
1) > + 가 됩니다.
그리고 "는 에서 가장 멀리 떨어진 점이어야 함"이 성립한다면,
2) > + 가 됩니다.
1), 2)를 합쳐보면,
> + > + + 이 되고,
가장 왼쪽 항과 가장 오른쪽 항만 보게 되면,
> + + 이므로
이는 모순입니다.
따라서 3-2번 경우는 존재할 수 없다고 할 수 있겠습니다.
결론적으로, 가능한 모든 경우의 수에 대하여 "임의의 정점 x으로부터 가장 먼 정점 y가 항상 지름의 양쪽 끝점 중 하나인가" 가 참인 것이 증명됐기 때문에, 위 방법이 올바르다는 것이 증명됩니다.
[ 참고한 블로그 ] : https://blog.myungwoo.kr/112
3. 코드로 구현하기
증명하는 과정이 복잡했지만 구현은 아주 간단합니다.
tree = [[] for _ in range(n+1)]
for _ in range(n-1):
p, c, w = map(int, input().split())
tree[p].append((c, w))
tree[c].append((p, w))먼저 입력되는 경로를 양방향으로 저장해줍니다. 트리의 형태이긴 하지만, 우리는 탐색 과정에서 자식 부모로도 이동해야 하기 때문입니다.
def dfs(start):
max = 0
idx = 0
visited = [False]*(n+1)
visited[start] = True
stk = [(start, 0)]
while stk:
curr = stk.pop()
if curr[1] > max:
max = curr[1]
idx = curr[0]
visited[curr[0]] = True
for child in tree[curr[0]]:
if not visited[child[0]]:
stk.append((child[0], child[1]+curr[1]))
return idx, max이제 어떤 정점에서 가장 먼 정점을 찾는 함수를 만들면 됩니다.
시작 정점부터 dfs 방식으로 정점에 방문할 때마다 이동한 거리를 누적하며 기록함으로써 가장 거리가 먼 정점을 찾아낼 수 있습니다.
idx, _ = dfs(1)
_, answer = dfs(idx)
print(answer)이제 임의의 정점 (여기서는 root)로부터 가장 먼 정점을 한번 찾고, 그 정점으로부터 가장 먼 정점을 찾았을 때 그 거리가 트리의 지름이 됩니다.
문제 해결!
결과 코드
import sys
input = sys.stdin.readline
n = int(input())
tree = [[] for _ in range(n+1)]
for _ in range(n-1):
p, c, w = map(int, input().split())
tree[p].append((c, w))
tree[c].append((p, w))
def dfs(start):
max = 0
idx = 0
visited = [False]*(n+1)
visited[start] = True
stk = [(start, 0)]
while stk:
curr = stk.pop()
if curr[1] > max:
max = curr[1]
idx = curr[0]
visited[curr[0]] = True
for child in tree[curr[0]]:
if not visited[child[0]]:
stk.append((child[0], child[1]+curr[1]))
return idx, max
idx, _ = dfs(1)
_, answer = dfs(idx)
print(answer)
