구간합, 누적합 [BOJ10986] 나머지합

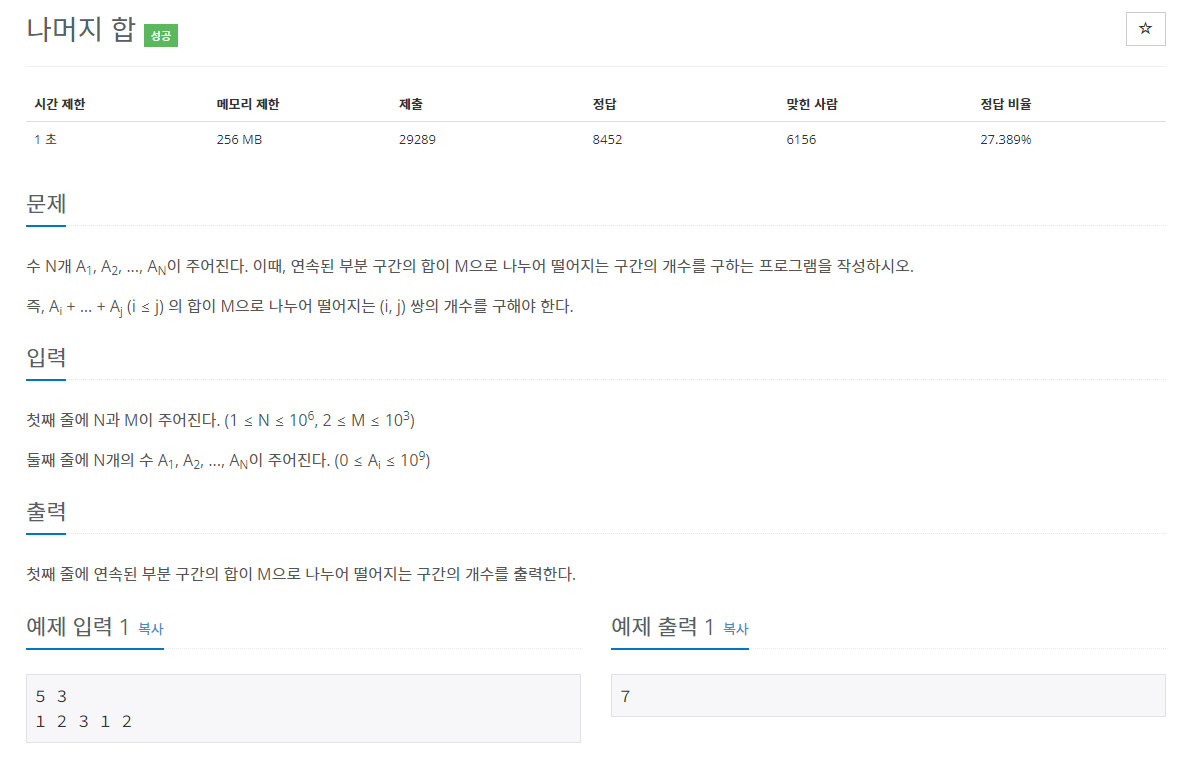
https://www.acmicpc.net/problem/10986

누적합 이용하기

굉장히 전형적인 문제라고 생각했는데 예상외로 생각할 부분들이 많았다.
구간합을 구하는 방법에는 경우에 따라 여러가지가 있겠으나,

기본적으로는 (i,j)까지의 구간합을 구한다고 하면 j까지의 누적합에서 sum[j]
i-1까지의 누적합을 빼는 방법이 있을 수 있다. sum[i-1]

위 문제도 누적합을 이용하여 풀이하면 풀 수 있는데,
중요한 건 10^6 만큼의 데이터의 수가 있기 때문에
10^6개 중 2개의 누적합을 골라서 빼는 방식으로 구간합의 경우의 수를 모두 구하면

O(n^2)의 시간복잡도가 나서 시간초과가 난다.

풀이

문제에서 sum[j]와 sum[i-1]이 M으로 나눴을 때의 나머지가 같은 경우에는 (i,j)구간합이 M으로 나눠 떨어진다.

예를 들어
M=3 이면 sum[j] = 7, sum[i-1]=4 일 때 차가 3 이므로 3으로 나눠떨이지는, 즉 답에 해당하는 구간합인데,

이는
4,7은 모두 3으로나눴을 때 나머지가 1 이므로 되는 것이다.

따라서 나머지를 count 하는 modCount 배열을 만들어 문제를 풀이하였다.

import java.io.*;
import java.util.*;

public class BOJ10986_나머지합 {

	static int N, M;
	static long sum;
	static long ans;
	static int[] mod;
	static int[] modCnt;

	public static void main(String[] args) throws NumberFormatException, IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		st = new StringTokenizer(br.readLine());
		N = Integer.parseInt(st.nextToken());
		M = Integer.parseInt(st.nextToken());

		mod = new int[(int) (N + 1)];
		modCnt = new int[(int) M];
		
		//0으로 카운트를 초기화해준다
		Arrays.fill(modCnt, 0);
		
		
		st = new StringTokenizer(br.readLine());
		// 누적합 배열을 채워주고, 바로 나눠떨어지는 경우에는 답에 ++을 해준다.
		for (int i = 0; i < N; i++) {
			int val = Integer.parseInt(st.nextToken());
			sum += val;
			int sumMod = (int) (sum % M);
			if (sumMod == 0)
				ans++;

			mod[i] = sumMod;
			modCnt[sumMod] += 1;
		}
		
		// 카운트 배열의 각 값에 따라서 2개를 뽑는 조합의 경우의 수를 답에 더해준다.
		for (int i = 0; i < M; i++) {
			long curModCnt = modCnt[i];
			if (curModCnt >= 2) {
				ans += (curModCnt * (curModCnt - 1) / 2);
			}
		}

		System.out.println(ans);

	}
}

유의점

전체 누적합을 담는 sum이 int 범위를 벗어날 수 있기 때문에 long 타입으로 바꿔줘야 한다.