(2-2) LU분해 / 행렬연산 & 선형조합 / 좌표계 변환 / 선형변환

Yongjoo Lee·2020년 12월 8일
ai mathmatrix decomposition
0

Programmers 인공지능 데브코스

목록 보기
9/33
post-thumbnail

3강: LU분해

행렬분해(matrix decomposition)

대표적인 행렬분해

  • LU 분해(LU Decomposition)
  • QR 분해(QR Decomposition)
  • 특이값 분해(SVD; Singular Value Decomposition)

LU 분해 → 가우스 소거법을 행렬의 형태로 나타낸 것

LU 분해

주어진 행렬을 아래의 형태를 가지는 두 행렬의 곱으로 나누는 행렬분해

A[∗∗∗∗∗∗∗∗∗]=L[∗00∗∗0∗∗∗]U[∗∗∗0∗∗00∗]\stackrel{\large\begin{bmatrix}* & * & * \\* & * & *\\* & * & *\end{bmatrix}}{\large A}=\stackrel{\large\begin{bmatrix}* & 0 & 0 \\* & * & 0\\* & * & *\end{bmatrix}}{\large L} \stackrel{\large\begin{bmatrix}* & * & * \\0 & * & *\\0 & 0 & *\end{bmatrix}}{\large U}
  • LL: lower triangular matrix(하삼각행렬)
  • UU: upper triangular matrix(상삼각행렬)

LU 분해를 이용해 Ax = b 문제를 아래와 같이 나타내면

Ax=b⇒(LU)x=b⇒L(Ux)=bAx = b \Rightarrow (LU)x = b \Rightarrow L(Ux) = b
⇒Ly=b,(단,y=Ux)\Rightarrow L\textcolor{red}{y} = b, (단, \textcolor{red}{y} = U\textcolor{blue}{x})

선형시스템을 다음과 같이 두 단계로 간단히 해결할 수 있다.

1) 전방대치법(Forward-substitution)

y\textcolor{red}{y} 구하기

L  y=bL\;\textcolor{red}{y} = b
[∗00∗∗0∗∗∗]L[y1⋮yn]y=[∗∗∗]b\stackrel{\large L}{\large\begin{bmatrix}* & 0 & 0 \\* & * & 0\\* & * & *\end{bmatrix}}\stackrel{\large \textcolor{red}{y}}{\large\begin{bmatrix}y_1 \\\vdots\\y_n\end{bmatrix}}\large=\stackrel{\large b}{\large\begin{bmatrix}*\\*\\*\end{bmatrix}}

2) 후방대치법(Back-substitution)

이전에 구한 y\textcolor{red}{y} 이용하여 x\textcolor{blue}{x} 구하기

U  x=yU \;\textcolor{blue}{x}=\textcolor{red}{y}
[∗∗∗0∗∗00∗]U[x1⋮xn]x=[y1⋮yn]y\stackrel{\large U}{\large\begin{bmatrix}* & * & * \\0 & * & *\\0 & 0 & *\end{bmatrix}}\stackrel{\large\textcolor{blue}{x}}{\large\begin{bmatrix}x_1 \\\vdots\\x_n\end{bmatrix}}\large =\stackrel{\large\textcolor{red}{y}}{\large\begin{bmatrix}y_1 \\\vdots\\y_n\end{bmatrix}}

LU 분해는 가우스 소거법의 전방소거법을 행렬로 코드화 한것!

A=P  L  UA=P\;L\;U

  • LL: 행렬 AA를 전방소거하는데 쓰인 치환(replacement)과 스케일링(scailing)에 대한 EROs를 기록해 둔 행렬

  • PP: 행렬 AA를 전방소거하는데 쓰인 교환(interchange)에 대한 EROs를 기록해 둔 행렬 (옵션)

  • UU: 행렬 AA를 전방소거한 후 남은 상삼각행렬(upper triangular matrix)

    EROs: elementary row operations; 기본행연산

LU 분해의 활용

  • 수치적 안정성

    : 선형시스템 Ax=bAx = b의 해를 역행렬 A−1A^{-1} 를 이용해 직접 구하는 것 보다 PLUPLU 분해를 이용하는 것이 좀 더 수치적으로 안정적

  • ⚡bb가 자주 업데이트 되는 경우

    : 선형시스템 Ax=bAx=b에서 행렬 AA는 고정되어 있고 bb가 자주 변하는 문제가 종종 있음. 이런 경우, 행렬 A를 미리 PLUPLU로 분해해두면 bb가 업데이트될 때마다 선형시스템의 해 xx를 실시간으로 구할 수 있음

4강: 행렬연산과 선형조합

행렬 표기법과 관련 용어

행렬(matrix): 직사각형 구조에 숫자들을 담아 놓은 구조이다. 각 숫자들은 행렬의 요소(Entry)라고 한다.

[311−22−4]\begin{bmatrix}3 & 1\\1 & -2\\2 & -4\end{bmatrix}

백터(vector): 하나의 행 혹은 하나의 열을 가지는 행렬, 행벡터(row vector)와 열벡터(column vector)가 있다.

[  2103  ][13]\begin{bmatrix}\;2 & 1 & 0 & 3\;\end{bmatrix}\begin{bmatrix}1\\3\end{bmatrix}

스칼라(scalar): 행과 열 모두 하나인 1 x 1 행렬

[ 4 ]\begin{bmatrix}\space4\space\end{bmatrix}

📌주요 표기법

A=[a11a11…a1j…a1na21a22…a2j…a2n⋮⋮⋮⋮ai1ai2…aij…ain⋮⋮⋮⋮am1am2…amj…amn]A=\begin{bmatrix}a_{11}&a_{11}&\dots&a_{1j}&\dots&a_{1n}\\a_{21}&a_{22}&\dots&a_{2j}&\dots&a_{2n}\\\vdots&\vdots&&\vdots&&\vdots\\a_{i1}&a_{i2}&\dots&a_{ij}&\dots&a_{in}\\\vdots&\vdots&&\vdots&&\vdots\\a_{m1}&a_{m2}&\dots&a_{mj}&\dots&a_{mn}\end{bmatrix}
  • 행렬 AA의 각 (ii,jj) 요소는 aija_{ij}로 나타낸다.
  • 행렬 AA를 간략히 표기할 때는 A=[ aij ]A=\begin{bmatrix}\space a_{ij} \space\end{bmatrix} 로 나타낸다.
  • 행렬 AA의 크기가 중요할 경우는 A=[ aij ]m×nA=\begin{bmatrix}\space a_{ij}\space\end{bmatrix}_{m\times n} 로 나타낸다.

벡터(Vector)

벡터는 아래의 x와 같이 볼드체 소문자로 표기한다.

📌주요 표기법

x=[x1x2⋮xn]\boldsymbol{x}=\begin{bmatrix} x_1\\x_2\\\vdots\\x_n\end{bmatrix}
  • 벡터라고 하면 일반적으로 열벡터(column vector)를 말한다.
  • nn-벡터는 nn개의 스칼라(scalar)로 구성된 벡터를 말한다.

전치행렬(Transpose Matrix)

m×nm \times n 행렬 AA에 대한 전치행렬 ATA^T는 AA의 행을 열로, AA의 열을 행으로 가지는 m×nm \times n 행렬이다.

즉, (AT)ij=(A)ji(A^T)_{ij} = (A)_{ji} 를 만족한다.

예)

A=[123456]    AT=[135246]A=\begin{bmatrix}1 & 2\\3 & 4\\5 & 6\end{bmatrix}\;\; A^T=\begin{bmatrix}1 & 3 & 5\\2 & 4 & 6\end{bmatrix}

영행렬(Zero matrix)

행렬의 모든 요소가 0이면, 해당 행렬을 영행렬(Zero matrix)라 하고 OO으로 표현한다.

A+O=O+A=AA+O=O+A=A

영행렬은 숫자의 0과 같은 존재로 행렬의 합에 대한 항등원 역할을 한다.

행렬의 합: 행과 열의 개수가 모두 같은 두 행렬 AA와 BB에 대해서, 각 (ii,jj) 요소의 합으로 정의된다.

정방행렬(Square matrix)

행과 열의 개수가 모두 n인 정사각형(Square) 모양의 행렬을 n차 정방행렬(square matrix)이라 한다.

A=[a11a11…a1j…a1na21a22…a2j…a2n⋮⋮⋮⋮ai1ai2…aij…ain⋮⋮⋮⋮am1am2…amj…amn]A=\begin{bmatrix}\colorbox{yellow}{$a_{11}$}&a_{11}&\dots&a_{1j}&\dots&a_{1n}\\a_{21}&\colorbox{yellow}{$a_{22}$}&\dots&a_{2j}&\dots&a_{2n}\\\vdots&\vdots&&\vdots&&\vdots\\a_{i1}&a_{i2}&\dots&\colorbox{yellow}{$a_{ij}$}&\dots&a_{in}\\\vdots&\vdots&&\vdots&&\vdots\\a_{m1}&a_{m2}&\dots&a_{mj}&\dots&\colorbox{yellow}{$a_{mn}$}\end{bmatrix}

특히, aii(i=1,2,…,n)a_{ii}(i=1,2,\dots,n)를 행렬 AnA_n의 주대각선(main diagonal)이라 한다.

항등행렬(Identity matrix)

주대각선이 1이고 나머지 요소는 모두 0인 n차 정방행렬을 항등행렬(Identity matrix)이라 한다.

In=[10…001…0⋮⋮⋮00…1]I_n=\begin{bmatrix}1&0&\dots&0\\0&1&\dots&0\\\vdots&\vdots&&\vdots\\0&0&\dots&1\end{bmatrix}

항등행렬은 숫자의 1과 같은 존재로 행렬의 곱에 대한 항등원 역할을 한다.

⭐행렬의 곱

m×rm \times r 행렬 A=[aij]A=\begin{bmatrix} a_{ij} \end{bmatrix} 와 r×nr \times n 행렬 B=[bij]B=\begin{bmatrix} b_{ij}\end{bmatrix} 가 있을 때, 두 행렬의 곱 AB는 아래와 같은

m×nm \times n 행렬 C=[cij]C=\begin{bmatrix} c_{ij} \end{bmatrix} 를 정의한다.

m×rr×nm×n[∗∗…∗⋮⋮⋮ai1ai2…air⋮⋮⋮∗∗…∗][∗…b1j…∗∗…b2j…∗⋮⋮⋮∗…brj…∗]=[∗…∗…∗⋮⋮⋮∗…cij…∗⋮⋮⋮∗…∗…∗]ABCm\times r \hspace{7.5em} r\times n \hspace{9.5em} m\times n\\\begin{bmatrix}*&*&\dots&*\\\vdots&\vdots&&\vdots\\a_{i1}&a_{i2}&\dots&a_{ir}\\\vdots&\vdots&&\vdots\\*&*&\dots&*\end{bmatrix}\begin{bmatrix}*&\dots&b_{1j}&\dots&*\\*&\dots&b_{2j}&\dots&*\\\vdots&&\vdots&&\vdots\\*&\dots&b_{rj}&\dots&*\end{bmatrix}=\begin{bmatrix}*&\dots&*&\dots&*\\\vdots&&\vdots&&\vdots\\*&\dots&c_{ij}&\dots&*\\\vdots&&\vdots&&\vdots\\*&\dots&*&\dots&*\end{bmatrix}\\A\hspace{9em}B\hspace{11.5em}C
cij=ai1b1j+ai2b2j+⋯+airbrjc_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\dots+a_{ir}b_{rj}

🔥행렬의 곱에서 반드시 숙지해야할 사항

  • 행렬 CC의 각 요소 cijc_{ij}는 '곱의 왼쪽 행렬 AA의 ii번째 행벡터'와 '곱의 오른쪽 행렬 BB의 jj번째 열벡터'의 내적(inner product)이다.

    • 따라서, 두 행렬의 곱 ABAB에 대해 AA의 열 개수와 BB의 행 개수는 일치해야 한다. (Am×r,Br×nA_{m \times r}, B_{r \times n})
    • 일반적으로 AB≠BAAB \not= BA이다. 왜냐하면 행과 열을 뽑아오는 방법이 다르기 때문이다.

  • 행렬의 곱은 병렬처리(parallel processing)로 가속할 수 있다!

    (행렬 AA의 각 행과 행렬 BB의 각 열은 연산에 독립적이다)

계층적 구조 이해하기 - 텐서

  • 스칼라
  • 벡터
  • 행렬
  • 텐서

스칼라 → 백터 → 행렬

스칼라는 숫자 하나로 구성되어 있다.

77

이 스칼라를 백터로 표현하면 1개의 구성요소로 이루어진 1-벡터가 된다.

[7]\begin{bmatrix}7\end{bmatrix}

이 스칼라를 행렬로 표현하면 1개의 구성요소로 이루어진 1 x 1 행렬이 왼다.

[7]1×1\begin{bmatrix}7\end{bmatrix}_{1\times 1}

벡터 → 행렬

벡터는 여러 숫자가 일열로 늘어선 구조이다.

[1234]\begin{bmatrix}1\\2\\3\\4\end{bmatrix}

이 벡터를 행렬로 표현하면 여러 모양의 행렬로 표현할 수 있다.

[1234]4×1[1234]2×2[1324]2×2[1234]1×4\begin{bmatrix}1\\2\\3\\4\end{bmatrix}_{4\times 1} \hspace{3em} \begin{bmatrix}1&2\\3&4\end{bmatrix}_{2\times 2} \hspace{3em} \begin{bmatrix}1&3\\2&4\end{bmatrix}_{2\times 2} \hspace{3em} \begin{bmatrix}1&2&3&4\end{bmatrix}_{1\times 4}

👉표현하고자 하는 행렬의 모양은 응용문제에 따라 결정한다.

행렬 → 벡터

행렬은 사각형 구조에 여러 숫자가 행과 열로 늘어선 구조이다.

[123456]2×3\begin{bmatrix}1&2&3\\4&5&6\end{bmatrix}_{2\times 3}

이 행렬을 벡터로 표현하면 6-벡터로 표현할 수 있다.

[123456][142536]\begin{bmatrix}1\\2\\3\\4\\5\\6\end{bmatrix}\hspace{3em}\begin{bmatrix}1\\4\\2\\5\\3\\6\end{bmatrix}

👉행렬을 벡터로 변환할 때, 행부터 혹은 열부터 읽을 것인지는 응용문제에 따라 결정한다.

텐서

텐서(tensor)는 스칼라, 벡터, 행렬을 아우르는 개념이다.

숫자가 늘어설 수 있는 방향이 k개면 k-텐서로 부른다.

  • 0-텐서: 스칼라
  • 1-텐서: 벡터 # 행 또는 열
  • 2-텐서: 행렬 # 행과 열

만일 아래의 TT의 각 요소 P(i,j)P(i,j)가 벡터라면, TT는 3-텐서로 볼 수 있다.

T=[P(1,1)P(1,2)P(1,3)P(1,4)P(2,1)P(2,2)P(2,3)P(2,4)P(3,1)P(3,2)P(3,3)P(3,4)P(4,1)P(4,2)P(4,3)P(4,4)]T=\begin{bmatrix}P\scriptsize(1,1)&P\scriptsize(1,2)&P\scriptsize(1,3)&P\scriptsize(1,4)\\P\scriptsize(2,1)&P\scriptsize(2,2)&P\scriptsize(2,3)&P\scriptsize(2,4)\\P\scriptsize(3,1)&P\scriptsize(3,2)&P\scriptsize(3,3)&P\scriptsize(3,4)\\P\scriptsize(4,1)&P\scriptsize(4,2)&P\scriptsize(4,3)&P\scriptsize(4,4)\end{bmatrix}

3-텐서의 대표적인 예는 컬러영상이다. P(i,j)P(i,j)가 3-벡터이면 RGB 영상을, 4-벡터이면 RGBA 영상을 나타낸다고 볼 수 있다.

🤔4-텐서는?

P(i,j)P(i,j) 가 행렬일 경우 4-텐서?

→ 컬러영상이 시간을 가지는 경우 (동영상)

분할행렬(Partitioned Matrix)

행렬을 조각(partition) 단위로 분할하여 생각해도 무방하다.

이런 관점에서 본다면, 행렬은 부분행렬(submatrix)로 이루어진 직사각형 구조로 확장해서 생각할 수 있다.

![https://velog.velcdn.com/images%2Fleeyongjoo%2Fpost%2F44743eba-dc78-43cf-b300-6bf1d0d0b4c2%2Fimage.png%5D(https%3A%2F%2Fimages.velog.io%2Fimages%2Fleeyongjoo%2Fpost%2F44743eba-dc78-43cf-b300-6bf1d0d0b4c2%2Fimage.png)

두 가지 관점

  1. 행렬은 행백터로 이루어진 열벡터이다.
  2. 행렬은 열벡터로 이루어진 행벡터이다.

(2번째 관점이 일반적!)

이렇게 행렬을 구조적으로 보는 방법은 분할행렬(partitioned matrix) 또는 블록행렬(block matrix)이라 한다.

분할행렬로 행렬의 곱 이해하기

선형조합(Linear Combination)

행렬 * 벡터 ⇒ 선형조합

행렬을 구조적으로 바라보는 가장 효과적인 방법은

행렬을 열벡터의 리스트로 보는 것이다.

A=[a11a11…a1na21a22…a2n⋮⋮⋮⋮⋮⋮am1am2…amn]=[a1a2…an]A=\begin{bmatrix}a_{11}&a_{11}&\dots&a_{1n}\\a_{21}&a_{22}&\dots&a_{2n}\\\vdots&\vdots&&\vdots\\\vdots&\vdots&&\vdots\\a_{m1}&a_{m2}&\dots&a_{mn}\end{bmatrix}=\large\begin{bmatrix}\bold a_1 & \bold a_2 & \dots & \bold a_n\end{bmatrix}

여기서 ai\bold a_i는 행렬 AA의 ii-번째 열벡터이다.

특히 각 열벡터는 mm-벡터이기 때문에, ∗∗m×n**m \times n 행렬은 mm-벡터가 nn개 있다**고 해석하면 된다.

Ax=bAx = b 에서

∗∗Ax**Ax는 행렬 AA가 가지고 있는 열벡터의 선형조합**이다.

선형대수에서는 이처럼 벡터들에 대한 가중치 합을 특히 선형조합(linear combination)이라 부른다.

👉Ax의 결과는 행렬 A가 가지고 있는 열벡터의 선형조합으로만 한계가 지어진다!

가중치 합을 했는데 우항을 절대로 만들어낼 수 없다?

→ 그것을 만족하는 x가 존재하지 않는다.

🔥(정리) 선형시스템 Ax=bAx=b 를 선형조합 관점에서 바라보기

행렬 AA의 열벡터의 가중치 합으로 선형조합할 때 벡터 bb를 만들 수 있는 가중치 조합이 존재한다면,

선형시스템 Ax=bAx=b 의 해는 존재한다. 그 해는 가중치 xix_i들로 구성된 xx이다.

열공간(Column Space)

행렬 A의 열벡터들에 대한 가능한 모든 선형조합의 결과를 모아 집합으로 구성할 수 있을 것이다.

이것을 열공간(Column Space)라고 하고 다음과 같이 표기한다.

col(A)col(A)
  • 선형시스템 Ax=b의 해가 존재하면(consistent), b∈col(A)b \in col(A)를 만족한다.
  • 선형시스템 Ax=b의 해가 없으면(inconsistent), b∉col(A)b \notin col(A)를 만족한다.

3차원 공간에서의 예제

  1. 행렬 AA의 col(A)col(A)는 3-차원 공간

    A=[−13212−321−2]A=\begin{bmatrix}-1&3&2\\1&2&-3\\2&1&-2\end{bmatrix}

    선형 시스템 Ax=bAx=b를 구성할 때

    어떤 3-벡터 bb를 이용하더라도 해당 선형시스템의 해는 존재한다.

  2. 행렬 AA의 col(A)col(A)는 xyxy-평면

    A=[−13212−3000]A=\begin{bmatrix}-1&3&2\\1&2&-3\\0&0&0\end{bmatrix}

    선형시스템 Ax=bAx=b를 구성할 때

    • xyxy-평면 상의 3-벡터 bb를 이용하면, 해당 선형시스템의 해는 존재하지만,
    • xyxy-평면을 벗어난 3-벡터 bb를 이용하면, 해당 선형시스템의 해는 존재하지 않는다.

5강: 좌표계 변환

벡터 : 크기와 방향을 가진 물리량

좌표계를 도입한 후, 벡터의 시작점을 원점으로 맞추고
끝점의 위치를 벡터 v의 수학적 표현으로 정의

좌표계(Coordinate System)

좌표계 : 좌표값 = 행렬 : 벡터

  • 행렬은 좌표계
  • 벡터는 좌표값
v=[ab]=[1001][ab]=a[10]+b[01]v = \begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix} = a\begin{bmatrix}1\\0\end{bmatrix} + b\begin{bmatrix}0\\1\end{bmatrix}

v 벡터는 xy-평면 상에서는 원점 (0,0)에서 시작하여 (a,b)에서 끝나는 벡터를 의미한다.

수식의 각 요소는 다음과 같다.

  • a[10]a\begin{bmatrix}1\\0\end{bmatrix} : x-축의 단위로 a번 전진함을 뜻함
  • b[01]b\begin{bmatrix}0\\1\end{bmatrix} : y-축의 단위로 b번 전진함을 뜻함
  • xyxy-좌표계 : [1001]\begin{bmatrix}1&0\\0&1\end{bmatrix}

각 항에서 동일한 지점을 표현하면 다음과 같다.

[v1v2][43]=[ab]\begin{bmatrix}\\\Large v_1&\Large v_2\\\\\end{bmatrix}\Large\begin{bmatrix}4\\3\end{bmatrix} = \Large\begin{bmatrix}a\\b\end{bmatrix}

  • (우항): e1e_1 과 e2e_2 를 기저(basis)로 가지는 표준좌표계에서의 좌표값은 (a, b)이다.

    [v1v2][43]=[1001][ab]\begin{bmatrix}\\\Large v_1&\Large v_2\\\\\end{bmatrix}\Large\begin{bmatrix}4\\3\end{bmatrix} = \Large\begin{bmatrix}1&0\\0&1\end{bmatrix}\Large\begin{bmatrix}a\\b\end{bmatrix}

    ⚡벡터만 있으면 그 앞에는 표준좌표계(Standard Coordinate System)라고 하는 항등행렬이 존재함
    (생략되었다고 생각)

  • (좌항): v1v_1 과 v2v_2 를 기저(basis)로 가지는 좌표계에서의 좌표값은 (4, 3)이다.

Ax=bAx = b에서

  • 행렬 AA는 좌표계
  • 벡터 xx는 AA 좌표계에서의 좌표값
  • 벡터 bb는 표준좌표계에서의 좌표값

좌표계 변환(Change of Basis)

Ax=b[1−122][21]=[16]Ax=b\\\begin{bmatrix}1&-1\\2&2\end{bmatrix}\begin{bmatrix}2\\1\end{bmatrix} = \begin{bmatrix}1\\6\end{bmatrix}

👉표준좌표계에서 어떤 벡터의 좌표값은 bb 인데, 그 좌표값이 AA 좌표계에서는 xx 이다.

x=A−1b[1214−1214][16]=[21]x=A^{-1}b\\\begin{bmatrix}\frac{1}{2}&\frac{1}{4}\\-\frac{1}{2}&\frac{1}{4}\end{bmatrix}\begin{bmatrix}1\\6\end{bmatrix} = \begin{bmatrix}2\\1\end{bmatrix}

👉표준좌표계에서 어떤 벡터의 좌표값은 xx 인데, 그 좌표값이 A−1A^{-1} 좌표계에서는 bb 이다.

A[v]A=B[v]BA[v]_{A} = B[v]_{B}

  1. BB를 기준으로(BB를 표준좌표계로 하고) [v]A[v]_{A} 의 좌표를 보고 싶으면

    B−1A[v]A=[v]BB^{-1}A[v]_{A}=[v]_{B}

  2. AA를 기준으로(AA를 표준좌표계로 하고) [v]B[v]_{B} 의 좌표를 보고 싶으면

    [v]A=A−1B[v]B[v]_{A}=A^{-1}B[v]_{B}

Ax = b는 "AA라는 좌표계에서 xx는 얼만큼, yy는 얼만큼을 가야 표준좌표계에서의 bb라는 좌표값에 도착하는지" 를 뜻함.

예제 # 1

벡터 vv가 표준좌표계에서 (2,3)(2, 3)으로 표현된다고 한다.

벡터 (3,1)(3, 1)과 (1,−2)(1, -2)를 기저벡터로 가지는 새로운 좌표계를 도입했을 때, 해당 벡터 vv는 어떤 좌표값을 가질까?

[311−2][v]=[23]\begin{bmatrix}3&1\\1&-2\end{bmatrix}\begin{bmatrix}\large v\end{bmatrix} = \begin{bmatrix}2\\3\end{bmatrix}

→ 가우스 소거법이나 역행렬을 이용하여 v(x1,x2)v(x_1, x_2)를 구하면 됨

🔥좌표계에 따른 좌표값이 달라도 동일한 지점이 될 수 있다!!!

예제 # 2

벡터 vv가 표준좌표계에서 (2,1,3)(2, 1, 3)으로 표현된다고 한다.

벡터 (1,3,1)(1, 3, 1)과 (1,−2,2)(1, -2, 2)를 기저벡터로 가지는 새로운 좌표계를 도입했을 때, 해당 벡터 vv는 어떤 좌표값을 가질까?

[113−212][v]=[213]\begin{bmatrix}1&1\\3&-2\\1&2\end{bmatrix}\begin{bmatrix}\large v\end{bmatrix} = \begin{bmatrix}2\\1\\3\end{bmatrix}

→ 가우스 소거법이나 역행렬을 이용하여 v(x1,x2)v(x_1, x_2)를 구하면 됨

좌표계가 열벡터 2개로 이루어져 있기 때문에 3차원 공간에 있는 2차원 평면만 다닐 수 있음

⭐3차원 좌표계를 가지지만 왜 2차원 좌표값을 가질까?

AA는 3차원 좌표계를 가지지만 2개의 백터로 이루어져 있다.

따라서 각각 다른 방향을 가리키는 두 벡터를 이용해서만 갈 수 있는 좌표값만 접근할 수 있다.

(두 벡터로 이루어진 평면)

그리고 2개의 열백터로 이루어져 있기 때문에 1개의 열백터 bb가 되기 위해서는 다음 식을 만족해야 한다.

3×2∗[v]=3×1[v]:2×13 \times 2 * [v] = 3 \times 1\\ [v]: 2 \times 1

🔥각 좌표값의 차원이 다를 수 있다!

6강: 선형변환

선형함수(Linear Function)

함수(Function)

입력이 들어가면 어떤 기능을 수행한 다음 출력을 반환

입력이 정의되는 집합 DD를 정의역(domain)

출력이 정의되는 집합 CC를 공역(codomain)이라 하며,

공역 중 실제 함수의 출력이 나오는 부분집합 f(x)f(x)를 치역(range)라고 한다.

함수 ff는 아래 그림과 같이 DD의 각 원소 xx가 CC의 한 원소 y(∋f(x))y( \ni f(x)) 에 대응되는 매핑룰(mapping rule)이다.

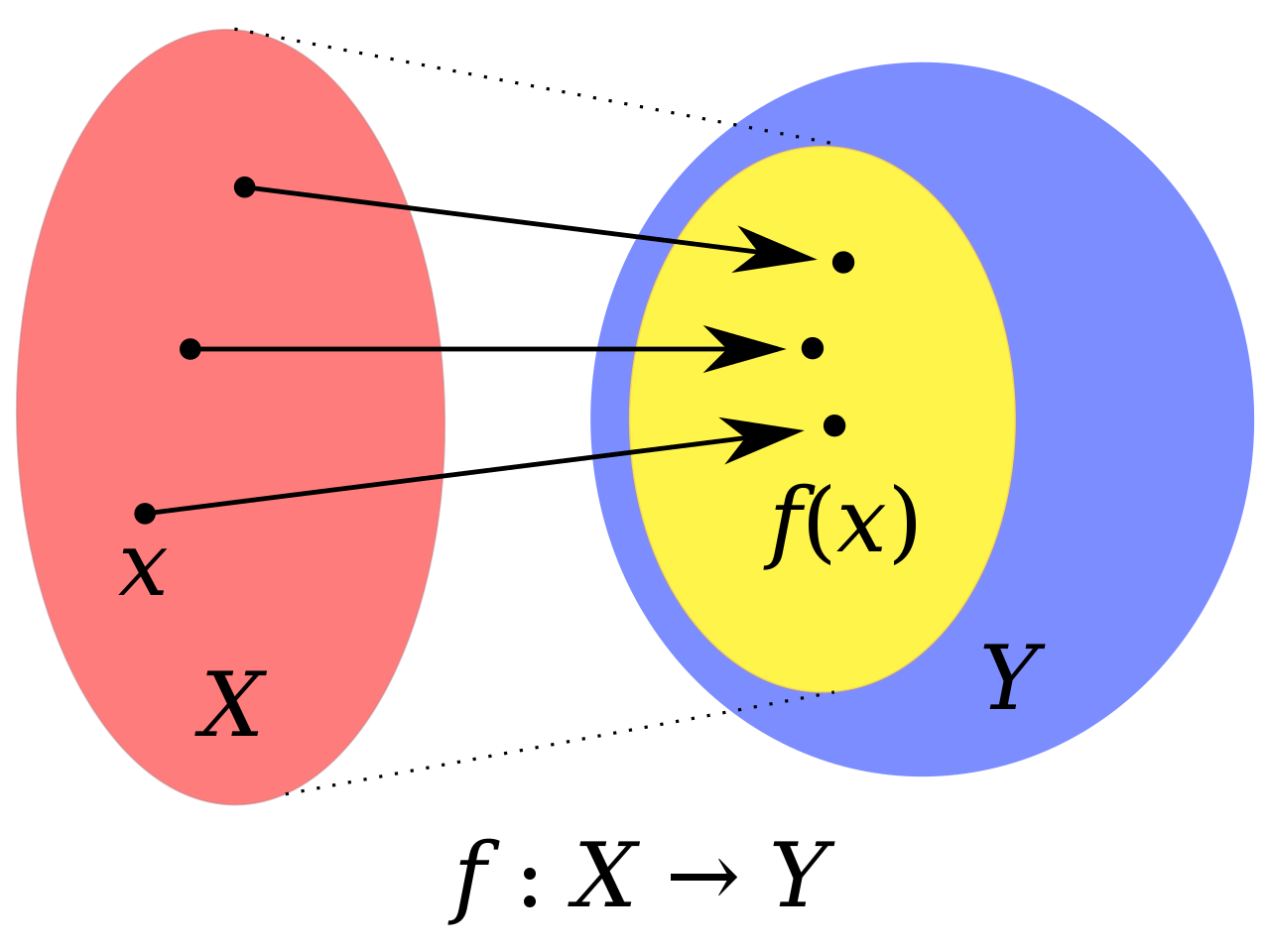
[그림출처: Wikipedia]

만일 함수 ff가 아래 두가지 조건을 만족하면 함수 ff를 선형함수(linear function)이라고 한다.

  1. f(x+y)=f(x)+f(y)f(x+y)=f(x)+f(y)
  2. f(cx)=cf(x)    (단,  c는  임의의  스칼라)f(cx)=cf(x)\;\;(단,\;c는\;임의의\;스칼라)

선형함수 : 일직선으로 나타나는 함수

행렬변환(Matrix Transformation)

변환(Transformation)

함수의 입력이 nn-벡터이고 출력이 mm-벡터인 함수 TT가 있을 때,

함수의 입출력이 벡터인 함수를 변환(Transformation)이라고 한다.

T:Rn→RmT:\mathbb{R^n}\rightarrow \mathbb{R^m}

만약 n=mn=m인 경우, 해당 변환을 연산자(operator)라고 한다.

m×nm\times n 행렬 AA에 대해 AxAx는 nn-벡터를 입력으로 받아 mm-벡터를 출력으로 내는 변환 Ax=TA(x)Ax = T_{A}(x)으로 볼 수 있다.

이 변환은 행렬이 정의하기 때문에 행렬변환(matrix Transformation)이라고 한다.

TA:Rn→RmT_{A}:\mathbb{R^n}\rightarrow \mathbb{R^m}

선형변환(linear Transformation)

그런데, 행렬변환은 다음의 선형함수 성질을 모두 만족하기 때문에 선형변환(linear Transformation)이다.

A(x+y)=A(x)+A(y)A(cx)=cA(x)A(x+y)=A(x)+A(y)\\A(cx)=cA(x)
  • 좌항의 ++ 는 nn-벡터의 덧셈, 우항의 ++는 mm-벡터의 덧셈
  • 좌항의 cxcx는 nn-벡터의 스케일링, 우항의 cA(x)cA(x)는 mm-벡터의 스케일링

👉 m×nm \times n 행렬은 nn-벡터를 입력으로 받아 mm-벡터를 출력을 내는 선형변환이며,

임의의 선형 변환은 행렬로 표현 가능하다. 즉, 행렬은 선형변환의 구현체이다.

표준행렬(Standard Matrix)

💡행렬변환이 입출력이 벡터로 정의된 선형함수라면, 해당 함수를 어떻게 코딩할 수 있을까?

다음 절차를 통해 원하는 방식대로 동작하는 행렬변환을 코딩할 수 있다.

  1. 구현하고자 하는 기능(function)의 입력과 출력이 벡터로 정의되는지 확인
  2. 구현하고자 하는 기능이 선형인지 확인
  3. 입력이 nn-벡터이고, 출력이 mm-벡터이면 m× nm \times\ n 표준행렬(standard matrix)을 구성

📌표준행렬 구하기

  • nn-차원 표준기저벡터 {e1,e2,…,en}\{e_1, e_2, \dots, e_n\} 를 생각한다. → 항등행렬
  • 각 nn-차원 표준기저벡터 eie_i에 대해, 우리가 원하는 기능을 동작시켜 얻은 결과인 mm-차원 벡터 T(ei)T(e_i)를 표준행렬의 각 열에 적는다.

😃표준행렬을 이용한 선형변환 코딩 예제

Q. 2차원 벡터를 입력으로 받아, 해당 벡터를 x-축에 프로젝션하는 기능을 구현해보자.

  • 구현하고자 하는 기능의 입력과 출력이 벡터로 정의되는지 확인

    입력으로 (3,2)(3, 2)인 2-벡터를 넣으면 출력으로 (3,0)(3, 0) 2-벡터로 정의됨

  • 구현하고자 하는 기능이 선형인지 확인

    출력이 x축을 그리기 때문에 선형임

  • m×nm \times n 표준행렬 구성

    1. 입력으로 첫 번째 기저벡터 (1,0)(1,0)를 넣어서 나오는 출력을 첫 번째 열벡터에 추가

      f([10])→[10]⇒T=[1∗0∗]f(\begin{bmatrix}1\\0\end{bmatrix})\rightarrow \begin{bmatrix}1\\0\end{bmatrix} \hspace{2em}\Rightarrow \hspace{2em}T=\begin{bmatrix}1&*\\0&*\end{bmatrix}

    2. 두 번째 기저벡터 (0,1)(0, 1)을 넣어서 나오는 출력을 두 번째 열벡터에 추가

      f([01])→[00]⇒T=[1000]f(\begin{bmatrix}0\\1\end{bmatrix})\rightarrow \begin{bmatrix}0\\0\end{bmatrix} \hspace{2em}\Rightarrow \hspace{2em}T=\begin{bmatrix}1&0\\0&0\end{bmatrix}
profile
Yongjoo Lee
하나씩 정리하는 개발공부로그입니다.
이전 포스트

(2-1) 선형시스템 / 가우스 소거법

다음 포스트

(2-3) 벡터 & 직교분해 / QR분해 / SVD, PCA / 최소 제곱법

0개의 댓글