
Parity Bit(패리티 비트)
정보 전달 과정에서 오류가 생겼는지 검사하기 위해 전송하고자 하는 데이터의 각 문자에 1비트를 더하여 전송한다.
- 패리티 비트는 2가지 종류(짝수, 혹수)로 나뉩니다.
- 8Bit 의 데이터를 전송할 때 패리티 비트가 뒤에 붙는데 비트 값에 따라 짝수 패리티(Even Parity) 와 홀수 패리티(Odd Parity)로 나뉜다.
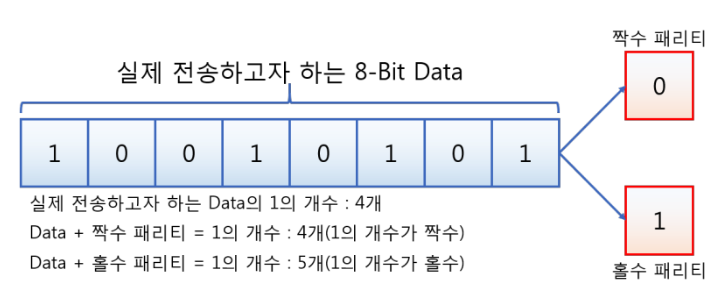
- 단, 짝수 패리티라고 비트값이 0이고 홀수 패리티라서 값이 1인건 아니다
- 실제 전송하고자 하는 비트들의 값중 1의 개수가 짝수면 짝수 패리티는 짝수를 유지하기 위해 0이 되고 홀수 패리티는 1의 갯수를 홀수로 맞추기 위해 1이 된다.
- 즉 짝수패리티는 1의 개수가 짝수가 되기 위해, 홀수 패리티는 1의 개수가 홀수가 되기 위해 비트값이 설정된다고 보면 된다.
사용하는 이유
- 통신을 할 때 데이터는 비트를 한개씩 전송하는데 어떠한 요인으로 인해 비트의 값이 변조되거나 중간에 전송이 실패하는 경우가 있다.
- 이때 송신측에서는 패리티비트를 이용하여 계산함으로써 데이터가 제대로 전송됐는지 확인할 수 있다.
- 패리티 비트는 주로 시리얼 통신의 거리가 상당히 멀 경우에 주로 적용 된다.
해밍 코드(Hamming Code)
해밍코드는 데이터 전송 시 1비트의 에러를 정정할 수 있는 자가 오류정정 코드를 말한다.
패리티비트를 보고, 1 비트에 대한 오류를 수정할 수 있다.
- 1비트는 오류 검출 및 정정이 가능하지만 2비트는 오류검출만 가능하고 정정이 불가능하다.
- 전송하는 데이터비트에서 추가되는 패리티 비트의 수는 아래와 같다.
2^p >= d + p + 1(p 는 패리티 비트의 수, d 는 데이터 비트의 수)
- 만약 데이터 비트의수가 4라면
2^p >= 5 +p가 되므로 패리티 비트의 수는 최소 4개 이다.

- 패리티 비트의 위치는
2^n(1,2,4,8,16...)에 위치한다. - 2^n 위치에 패리티 비트는 n번씩 건너뛰어 결정된다 !!
정보비트를 해밍코드로 변환 및 오류 검출
- 정보비트
1011에 홀수 패리티 비트를 적용하여 해밍코드를 변환한다고 하자. - 우선 패리티 비트는 1,2,4,8.. 과 같이 2의n승에 위치에 오고 데이터 비트가 4개이므로 패리티 비트의 수는 최소 4개이다.
p p 1 p 0 1 1로 변환된다(p는 패리티 비트)- 1 번째 패리티 비트는
p 1 0 1의 홀수 패리티가 되야 하므로 1 이 된다. - 2 번째 패리티 비트트
p 1 1 1의 홀수 패리티가 되야 하므로 0 이 왼다. - 3 번째 패리티 비트트
p 0 1 1의 홀수 패리티가 되야 하므로 1 이 온다. - 즉,
1011의 홀수패리티 해밍코드는1 0 1 1 0 1 1이 된다.만약
1011의 해밍코드인1011011이 통신중간에 오류로 인해1111011로 변하면 송신측에서는 아래와 같이 검사 및 수정할 수 있다.2^n 번째 패리티 비트를 역순으로 나열하여 수정할 부분을 도출해 낼 수 있다 !!
- 첫번째 패리티 비트 :
1101(정상) = 0 - 두번쨰 패리티 비트 :
0111(비정상) = 1 - 세번째 패리티 비트 :
1011(정상) = 0 - 역순으로
010해리티 비트를 10진수로 변환하면 2번째 자리에서 오류가 났음을 송신측에서 알 수 있다.
- 첫번째 패리티 비트 :