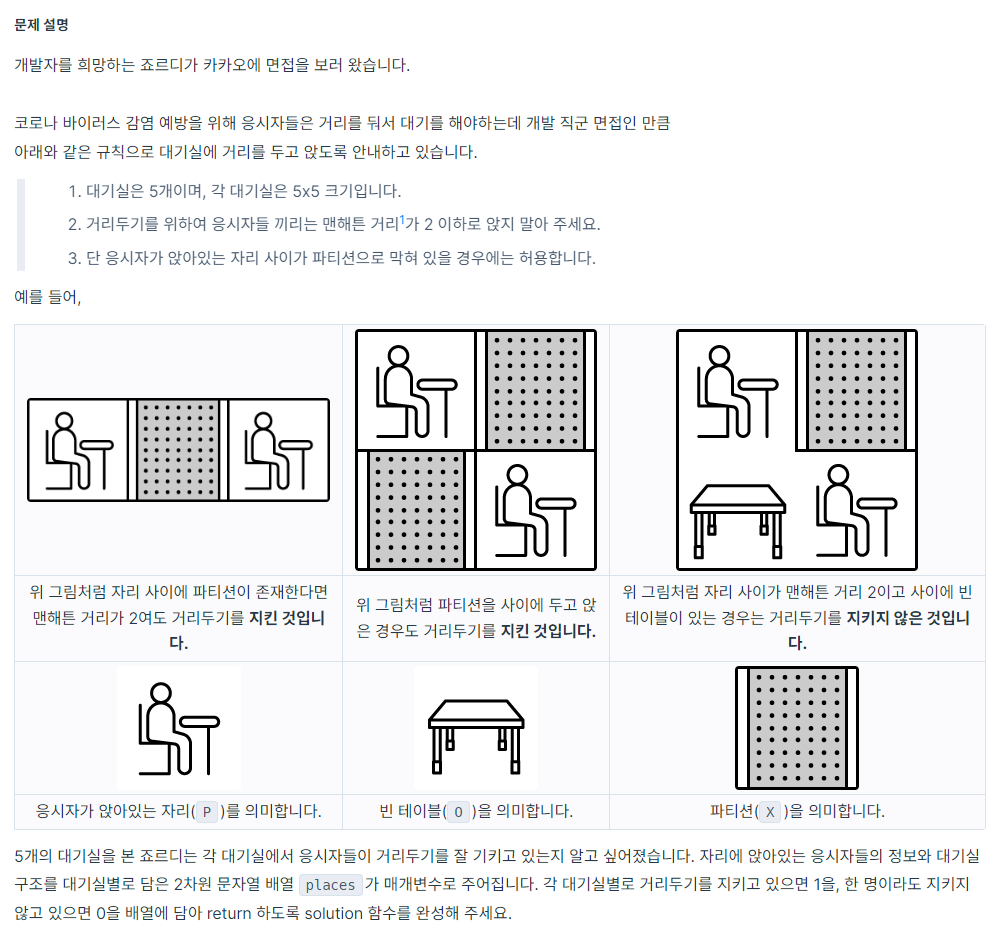
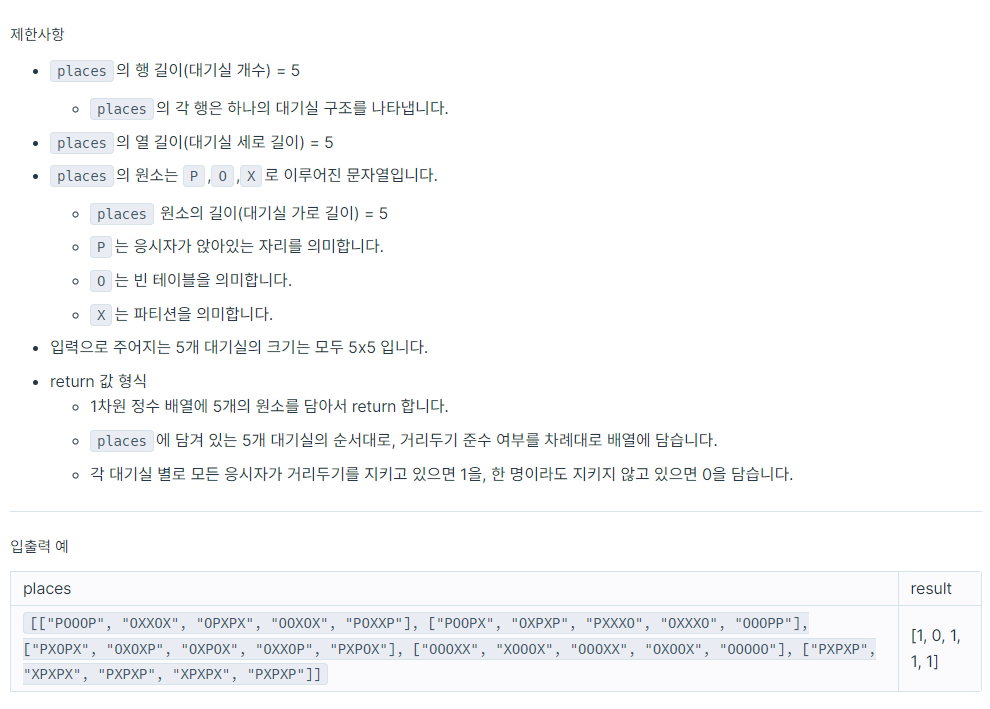
📒문제
📌정답 풀이
나름 BFS/DFS 공부는 정말 열심히 했기 때문에 이 문제도 딱 보자마자 BFS/DFS로 푸는 문제라는 생각이 들었다. 두 참석자가 대각선으로 위치할 때 파티션이 있는지 없는지 판단하는 데서 조금 버벅이긴 했지만 결국 문제는 풀 수 있었다.
이 코드는 어쨌거나 정답 코드이므로 조금 설명을 자세히 써볼까 한다.
from collections import deque
def solution(places):
def bfs(r, c):
q = deque() #BFS를 수행할 Queue
visit = [[False for _ in range(5)] for _ in range(5)]
#BFS를 수행할 방향을 미리 설정
d_r = [1, -1, 0, 0]
d_c = [0, 0, 1, -1]
#시작점은 (r,c)이므로, queue에 넣고 visit[r][c]=True
q.append((r, c))
visit[r][c] = True
while(q):
T = q.popleft()
c_r, c_c = T[0], T[1]
visit[c_r][c_c] = True
#BFS 수행하며 queue에서 pop하고, pop한 위치에 대해선 visit = True수행
for i in range(4):
n_r = c_r + d_r[i]
n_c = c_c + d_c[i]
# BFS 수행할 방향을 더해줌
if n_r < 0 or n_c < 0 or n_r > 4 or n_c > 4: continue # 맵밖을 나간다면 조건에 맞지 않으므로 제외
if visit[n_r][n_c] == True: continue # 이미 방문한 위치라면 굳이 더 방문할 이유 없으므로 제외
if abs(n_r-r) + abs(n_c-c) <= 2 and room[n_r][n_c] == 'P':
# 만일 맨해튼 거리가 2이하라면, 파티션이 중간에 가로막고 있는지 판단해야 함.
# 가로 막고 있다면 거리두기를 지킨 거지만, 그렇지 않다면 지키지 않은 것임.
if n_r == r or n_c == c:
if room[(n_r+r)//2][(n_c+c)//2] != 'X': return False
# 만일 행이나 열 중 하나가 같다면 (가로, 세로로 두 참석자가 배열되어 있다면)
# 그 중간은 무조건 파티션이어야만 거리두기를 지킬 수 있음.
else:
if room[n_r][c] != 'X' or room[r][n_c] != 'X': return False
# 만일 행과 열이 전부 다르다면 이 두 참석자는 대각선으로 배열되어 있는 상태
# 2*2에서 참석자를 제외한 2칸은 모두 파티션이어야 거리두기를 지킬 수 있음.
elif room[n_r][n_c] == 'O':
q.append((n_r, n_c))
# 'O'라면 BFS의 길이므로 queue에 append
return True
result = []
for place in places:
room = []
for p in place:
room.append(list(p))
s = True
for i in range(5):
for j in range(5): #이중 for문을 돌면서 해당 요소가 참석자라면, 그 위치부터 BFS 수행
if room[i][j] == 'P':
s = bfs(i, j)&s
if s: result.append(1)
else: result.append(0)
return result이중 for문을 통해 방을 돌면서 만일 해당 요소가 참석자라면 그 위치로부터 bfs를 수행한다.
자세한 설명은 주석에 달아 놓는다.
📌모범 풀이
내가 이 문제를 버벅였던 이유는 대각선으로 위치한 참석자들의 조건을 전부 고려하지 못했기 때문이다. 그래서 당연히 대각선에 위치한 참석자를 고려하는게 관건이라고 생각했던 문젠데, 인터넷 풀이를 보니 대각선을 오히려 고려하지 않는게 더 쉽게 풀 수 있다고 한다.
# 출처: https://velog.io/@hammii/ velog참조
from collections import deque
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
def bfs(place, x, y):
visited = [[False] * 5 for _ in range(5)]
q = deque()
q.append((x, y, 0))
visited[x][y] = True
while q:
x, y, cost = q.popleft() #이렇게도 쓸 수 있는 건 처음 알았다...
if cost == 2:
continue
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < 5 and 0 <= ny < 5:
if visited[nx][ny]:
continue
# cost==1 지점에서 다음으로 가는 과정에서 미리 거리두기 준수 여부를 판단.
if place[nx][ny] == 'P':
return False
if place[nx][ny] == 'O':
q.append((nx, ny, cost + 1))
visited[nx][ny] = True
return True
def solution(places):
answer = []
for place in places:
p = [list(place[i]) for i in range(5)] # 대기실
flag = True
for i in range(5):
for j in range(5):
if p[i][j] == 'P':
if not bfs(p, i, j): # 거리두기 안 지켰을 경우
flag = False
if not flag:
break
if flag:
answer.append(1)
else:
answer.append(0)
return answer이 코드는 거리까지 bfs queue에 담았다.
-
q에서 pop한 정점이 cost==2일때, 이 지점은 빈 책상이라는 것을 암묵적으로 의미한다. (queue에 append되는 때는 빈 책상일때 뿐이기 때문)
-
이때 여기서 continue해주는 부분은, 이 이상 BFS를 수행한다면 이후 방문하는 지점들은 무조건 맨해튼 거리가 2를 넘으므로, 그 지점이 X이든, O이든, P이든 거리두기 준수 여부에 영향을 미치지 않는다.
-
이 코드는 cost==1 지점에서 다음으로 가는 과정에서 미리 거리두기 준수 여부를 판단한다. 따라서 대각선으로 참석자들이 위치할 때 cost==1지점에서 그 다음 지점에 'P'가 있다면 이는 거리두기 미준수로 볼 수 있다.
-
만일 대각선으로 위치한 참석자 사이가 모두 파티션으로 막혀있다면, 맨해튼 거리(절대적인 거리)는 2지만 애초에 'O'인 지점만을 방문하기 때문에 cost==2보다 멀리 있는 지점은 애초에 탐색조차 하지 않는다.
-
따라서 막혀있다면 아예 고려하지 않고, 안 막혀있다면 다음 지점에서 탐색을 해주기 때문에 대각선을 굳이 따로 생각해 줄 이유가 없다.
