[PS, Algorithm] - 수식 최대화 (2020 카카오 인턴십, LEVEL 2) 🎈

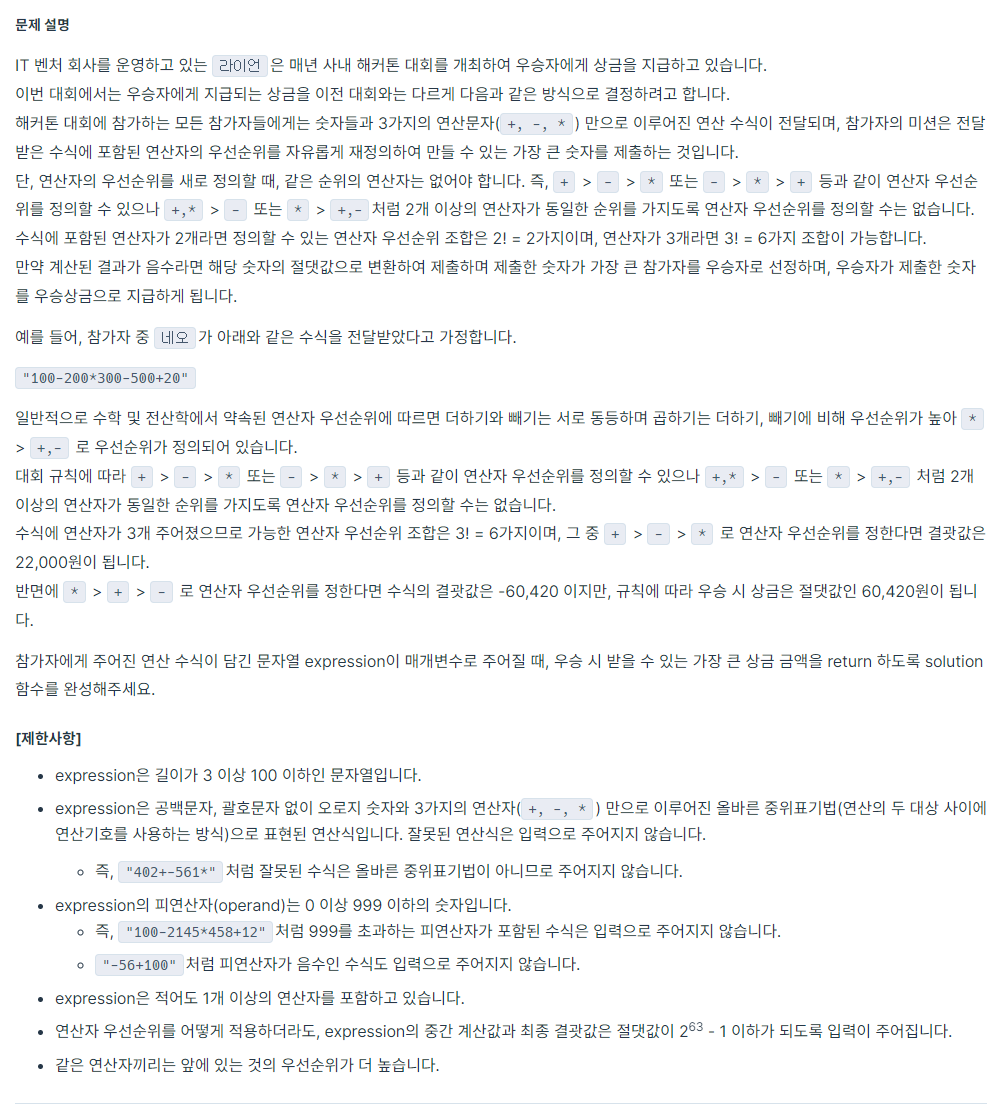
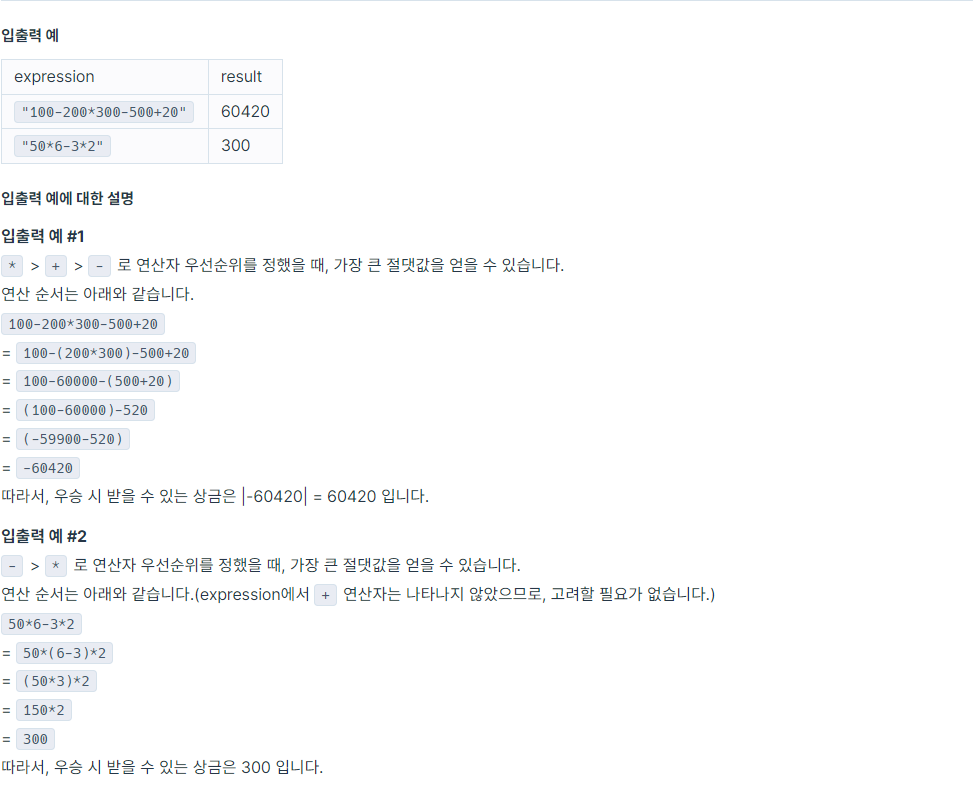
📒문제

---

📌풀이

from itertools import permutations as permu
from collections import defaultdict

def solution(expression):
    def convert(expression):
        result = []
        stack = [] #연산자 담기 위한 스택
        
        for exp in expression:
            if exp.isnumeric(): result.append(exp) # 피연산자면 그대로 append
            else:
                if not stack: stack.append(exp) # 스택이 비어있으면 바로 연산자 스택에 추가
                else:
                    if pr[stack[-1]] < pr[exp]: stack.append(exp) # 스택 top의 연산자 순위가 현재 연산자 순위보다 낮다면 걍 stack에 넣기
                    else: # 스택 top의 연산자 순위가 현재 연산자 순위보다 높다면 top이 더 낮아질때까지 pop하고 걍 stack에 넣기
                        while stack and pr[stack[-1]] >= pr[exp]:
                            d = stack.pop(-1)
                            result.append(d)
                        stack.append(exp)
        if stack:
            while stack:
                d = stack.pop(-1)
                result.append(d)
    
        return result
    
    def calculate(expression):
        stack = []
        for exp in expression:
            if exp.isnumeric(): stack.append(int(exp))
            else:
                n2 = stack.pop(-1)
                n1 = stack.pop(-1)
                
                if exp == "+": stack.append(n1+n2)
                elif exp == "-": stack.append(n1-n2)
                elif exp == "*": stack.append(n1*n2)
                
        return stack[-1]

    cases = list(permu(range(3), 3))
    pr = defaultdict(int) # 각 연산자의 우선순위 저장
    
    expression =  expression.replace("-", " - ").replace("+", " + ").replace("*", " * ").split()
    new_expression = []
    
    answer = 0
    for c in cases:
        pr["+"], pr["-"], pr["*"] = c
        new_expression = convert(expression)    
        
        tmp = abs(calculate(new_expression))
        if answer < tmp:
            answer = tmp
    
    return answer

내가 생각한 아이디어는

• 우선순위는 순열을 사용해서 구현하자.
• 연산자 우선순위에 따른 계산은 후위표기식의 원리를 사용하자.

였다.

순열은 어차피 연산자는 여기서 3개밖에 존재하지 않기에 기껏해봐야 6개의 case밖에 존재하지 않는다. 그리고 이런 계산식과 관련된 문제는 스택을 이용하여 풀었었기 때문에 후위표기식을 사용하야겠다고 생각했다.

🎈 얻어 갈 점

이 문제를 풀면서 얻어갈 수 있었던 것은

• 문자열을 여러개의 기준으로 분리하려고 할 때 정규표현식을 사용할 수도 있지만 replace를 통해서 이해하기 쉽게 분리할 수도 있다는 점

    expression =  expression.replace("-", " - ").replace("+", " + ").replace("*", " * ").split()
    # -, +, *을 기준으로 분리함

• 중위표기식(우리가 일반적으로 볼 수 있는 피연산자와 연산자가 서로서로 뒤섞인 형태의 수식)에서 후위표기식으로의 변환 방식

특히 중위표기식->후위표기식의 변환 방식은 1학년 자료구조 시간에 배웠던 게 어렴풋이 기억이 났었는데, 정작 구현해보려 하니 잘 생각이 안나 다시 공부했다.

🎈 중위 표기식 -> 후위 표기식 변환

연산자의 배치는 스택을 통해 해준다는 것이 변환의 핵심이다.

• 피연산자는 어떤 수든 상관없이 변환식에 더해준다.
• 연산자는 우선순위에 따라 달라지게 되는데,
  1. 스택에 연산자가 없으면 그냥 스택에 넣어준다.
  2. 만일 탐색한 연산자의 우선순위가 스택의 top연산자의 우선순위보다 높다면, 그냥 스택에 넣어준다.
  3. 만일 탐색한 연산자의 우선순위가 스택의 top연산자의 우선순위보다 낮거나 같다면, 탐색 연산자의 우선순위가 스택 top 우선순위보다 높을때까지 스택에서 pop해준다. pop한 연산자는 pop한 순서대로 변환식에 더해준다.

---

📌모범 풀이

# 참조 사이트: https://2hs-rti.tistory.com/entry/%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%A8%B8%EC%8A%A4-Lv2-%EC%88%98%EC%8B%9D-%EC%B5%9C%EB%8C%80%ED%99%94-%ED%8C%8C%EC%9D%B4%EC%8D%AC

from itertools import permutations as perm
from collections import deque


def solution(expression):
    answer = 0
    for priority in list(perm(['+', '-', '*'], 3)):
        answer = max(answer, abs(make_result(priority, expression)))
    return answer


def make_result(priority, expression):
    # arr 만들기
    arr = deque()
    num = ''
    for k in expression:
        if k.isdigit():
            num += k
        else:
            arr.append(num)
            num = ''
            arr.append(k)
    arr.append(num)
    # 계산
    for op in priority: # 우선순위가 높은 연산자를 기준으로
        stack = []
        while len(arr) != 0:
            temp = arr.popleft()
            if temp == op: # 그 연산자라면 eval함수를 통해 먼저 그 연산자 처리 후 계산값을 stack에 넣어둔다.
                result = str(eval(stack.pop()+op+arr.popleft()))
                stack.append(result)
            else:
                stack.append(temp) # 그 연산자가 아니라면 걍 스택에 일단 넣어둔다.
        arr = deque(stack) #연산자 처리 완료, 그다음 연산자 처리를 위해 stack에 남겨둔 애들을 arr에 복사
    return int(arr.pop())

중위표기식 후위표기식 사실 몰라도 풀 수 있는 문제긴 했다. 순열로 연산자의 우선순위를 정하는 건 똑같고, 그저 우선순위 높은 연산자만 먼저 연산해주고 나머지는 스택에 넣어둔 다음, 그 다음 우선순위가 높은 연산자 기준으로 먼저 연산해준다.....

생각보다 간단하게 풀 수 있는 문제였다.