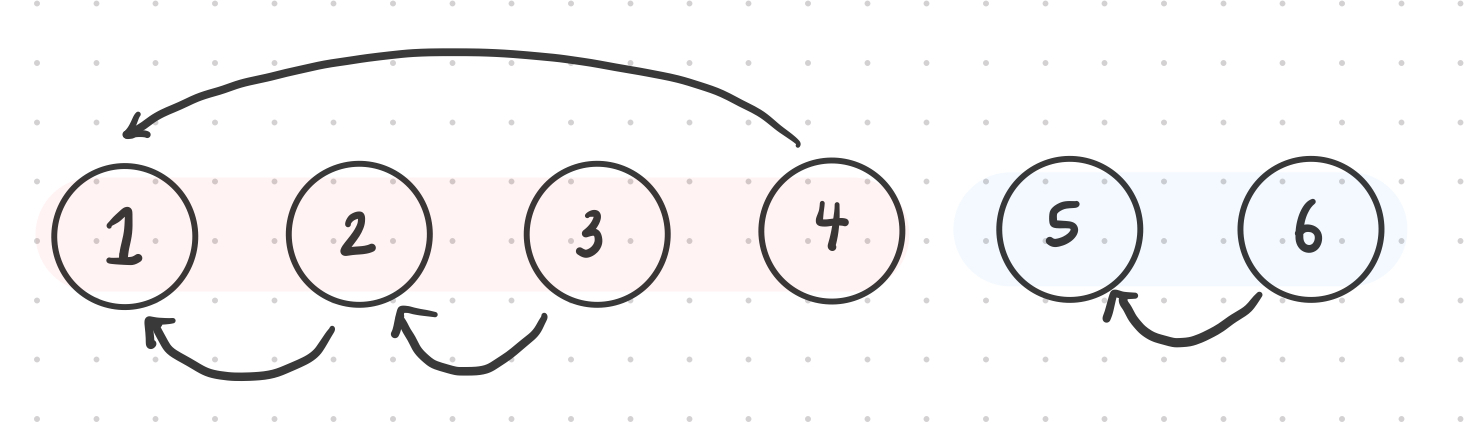
📒문제
🎈풀이
from collections import defaultdict
def solution(n, wires):
def dfs(start, visited):
visited.append(start)
for i in graph[start]:
if i not in visited:
dfs(i, visited)
return visited
answer, tr = 10000000, 0
for i in range(n-1):
graph = defaultdict(list)
for j in range(n-1):
if j == tr: continue
else:
graph[wires[j][0]].append(wires[j][1])
graph[wires[j][1]].append(wires[j][0])
n1 = len(dfs(1, []))
n2 = n - n1
if answer > abs(n1-n2): answer = abs(n1-n2)
tr += 1
return answern이 100이하라서 그냥 완전탐색으로 풀어도 상관이 없겠다고 판단했다.
tr값을 하나씩 올리면서 임시적으로 무시할 wire를 선택해주었고, 그걸 바탕으로 graph를 재구성한 후 dfs를 통해 첫 번째로 만들어지는 그래프의 사이즈를 파악해주고, 두 번째 그래프는 전체 사이즈에서 첫 번째 그래프 사이즈만큼 빼주어 사이즈를 구한 후 최소 차를 구해주었다.
사실 n이 훨씬 컸으면 O(n^2) 시간 복잡도를 가지는 이 코드 특성상 통과가 안 됐을 것 같은데, 다른 방법이 있는지도 살펴보아야 겠다.
🎈다른 풀이
union-find 알고리즘을 통해서도 문제를 풀 수 있다고 하는데, 이 알고리즘에 대한 기억이 가물가물해서... 오늘 일단 정리부터 하려고 한다.
Union-find 알고리즘은 서로소 집합, 상호배타적 집합 알고리즘 (Disjoint set)이라고도 불리는데, 여러 노드 중 두 노드가 서로 같은 그래프 상에 속하는지를 판별하는 알고리즘이다.
📢 1. 초기화 단계: 각 노드의 부모 노드를 담는 배열 parent를 각자 자신으로 초기화 하는 과정
📢 2. Union 단계: 서로 연결된 노드들을 하나의 그래프로 합치는 과정 (Parent 배열로 표현)
ex) union 1, 3 과 union 2, 4연산이 수행되면 1, 3은 같은 그래프이며 2, 4가 같은 그래프에 위치한다.
📢 3. Find 단계: Union 단계에서 만들어진 그래프를 통해 노드가 같은 그래프에 속하는지 확인하는 과정
위와 같은 그래프가 있다고 가정해 보면, (1 - 2, 2 - 3, 1 - 4가 연결되어 있고, 5 - 6으로 연결되어 있는 그래프)
📢 1. 부모 테이블 초기화
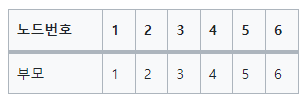
- parent 배열의 초기 값은 자기 자신을 가지도록 초기화한다.
📢 2. Union 연산
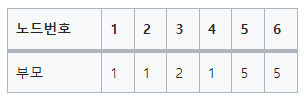
- 각 노드의 루트 노드(가장 꼭대기 층에 있는 노드)를 찾아, 더 큰 값의 루트 노드를 갖는 노드의 parent를 더 작은 루트노드로 변경
ex) 초기화 테이블 단계에서 union 1, 4연산시, 1의 루트노드는 1, 4의 루트노드는 4이므로, 4의 parent를 1로 변경
📢 3. Find 연산
- 그래프의 최종적인 루트 노드의 parent값은 자기 자신과 같으므로, find 함수는 재귀를 통해 루트노드 값을 찾아 반환
ex) 노드 4의 루트 노드는 1이고, 노드 6의 루트 노드는 5임 (1과 5의 parent값이 각각 자기 자신 1, 5) 따라서 두 개의 parent값은 서로 같지 않으므로 해당 노드들은 서로 다른 그래프임.
🎈구현 코드
INF = int(1e9)
from collections import Counter
def solution(n, wires):
def find(a):
if parent[a] != a:
parent[a] = find(parent[a])
return parent[a]
def union(a, b):
a = find(a)
b = find(b)
if a < b:
parent[b] = a
else:
parent[a] = b
answer = INF
for i in range(n-1):
parent = [a for a in range(n+1)]
for j in range(n-1):
if j == i: continue
else:
union(wires[j][0], wires[j][1])
result = []
for j in range(1, len(parent)):
result.append(find(j))
n1 = max(list(Counter(result).values()))
n2 = n - n1
if answer > abs(n1-n2): answer = abs(n1-n2)
return answer📢 union-find 알고리즘의 경로 압축
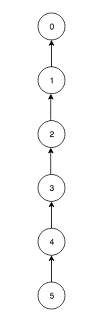
- union연산만 진행했을 때의 parent의 값은 최종적인 루트 노드라고 할 수 없다.
위의 그래프의 경우에는 최종 루트 노드는 0이지만, union연산을 진행 했을 때 각 노드의 parent값은 자기 자신보다 한 단계 위의 상위 노드를 가리킨다.- 따라서 경로 압축을 해주어야 하는데, union으로 얻어낸 parent배열의 각 요소들을 find에 다시 넣어 경로 압축을 해줄 수 있다.
def find(a): if parent[a] != a: parent[a] = find(parent[a]) return parent[a]union연산후 최적화된 find를 한번더 돌려주면 노드들의 최종적인 root배열로 정리가 되게 된다. (위의 그래프의 경우 노드들의 모든 parent값이 0으로 변경됨)
union find 알고리즘을 활용해서 그래프 내의 사이클을 판별할 수 있다.
📢 2. union-find 알고리즘으로 사이클 판별하기
이걸 보고 한방에 이해가 됐다...