[PS, Algorithm] - 후보키 (2019 KAKAO BLIND RECRUITMENT, LEVEL 2)

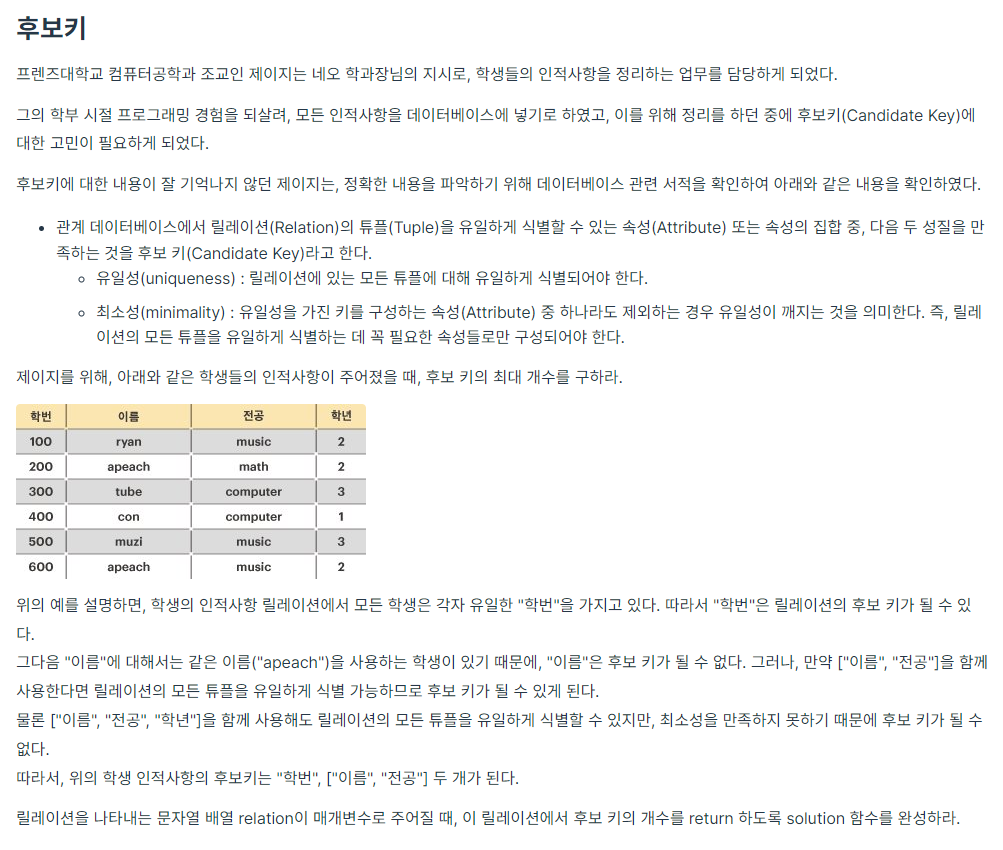
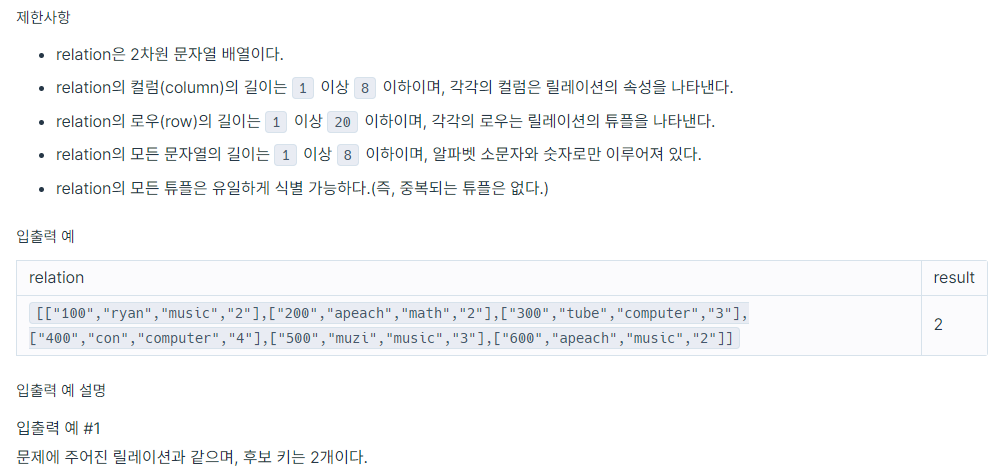
📒문제

---

📌풀이

from itertools import combinations as combi

def solution(relation):
    n_tuple = len(relation)
    n_attr = len(relation[0])
    
    candidates = []
    for i in range(1, n_attr+1):
        candidates.extend(combi(range(n_attr), i)) 
    
    T = []
    for c in candidates:
        tmp = [tuple(item[key] for key in c) for item in relation] #인덱스를 객체로 만들어준다.
        if len(set(tmp)) == n_tuple: T.append(c)
    
    rm = set()
    for i in range(len(T)):
        for j in range(i+1, len(T)):
            if set(T[i]) & set(T[j]) == set(T[i]): rm.add(T[j])
            
    return len(set(T) - rm)
    

1.

• 먼저, tuple의 개수(행의 개수), attribute의 개수(열의 개수)를 각각 구해 n_tuple, n_attr에 각각 저장해 주었다.

    n_tuple = len(relation)
    n_attr = len(relation[0])

2.

• extend 함수를 통해 인덱스로 표현한 속성을 선택하는 모든 경우의 수를 담는다.

	candidates = []
    for i in range(1, n_attr+1):
        candidates.extend(combi(range(n_attr), i))

1. append 함수는 요소 그 자체를 리스트에 더하지만,

list1 = [1, 2]
list1.append([1,2,3]) #list1 = [1, 2, [1,2,3]]

2. extend 함수는 요소 내부의 모든 요소를 전부 끄집어내어 리스트에 더한다.

list1 = [1, 2]
list1.extend([1,2,3]) #list1 = [1, 2, 1, 2, 3]

3.

tmp = [tuple(item[key] for key in c) for item in relation] 
# c = (0, 1)일 때 
#tmp = [('100', 'ryan'), ('200', 'apeach'), ('300', 'tube'), ('400', 'con'), ('500', 'muzi'), ('600', 'apeach')]
if len(set(tmp)) == n_tuple: T.append(c)
# 중복되는 경우가 있다면 uniqueness에 위배

tmp가 왜 저렇게 되는지는 주석으로 처리된 실제 케이스를 보면서 이해하는 게 편하다.

• c = (0, 1)이라면, 이 말은 곧 속성 0번과 속성 1번(여기선 학번, 이름)을 사용하겠다는 말과 같다.
• for item in relation으로 모든 tuple을 순회하고, for key in c로 모든 key를 순회하면서 최종적인 키를 담는다.

그 후 set로 중복을 제거하여 만일 길이가 다르다면 중복되는 튜플이 존재했다라는 의미이므로, 유일성에 위배된다.

4.

    rm = set()
    for i in range(len(T)):
        for j in range(i+1, len(T)):
            if set(T[i]) & set(T[j]) == set(T[i]): rm.add(T[j])
            
    return len(set(T) - rm)

그 후 유일성을 만족하는 후보군 T에서, for문을 돌며 모든 후보군과 교집합 연산을 하는데, 만일 교집합이 자기자신이 나온다면 이는 곧 상대 후보군은 최소성을 만족하지 못함을 의미한다. 따라서 제거할 후보군 rm에 넣고, 결과값을 구할 때는 T와 rm의 차집합이 최종적으로 구하고자 하는 정답이 된다.

---

문제를 풀면서 느낀 거지만 아직도 파이썬 list comprehension이나 STL함수 쓰는 능력이 아직 많이 부족한 것 같다. extend함수나, tmp 구하는 부분은 복잡하긴 하지만 충분히 생각해 낼 수 있었던 내용인데 그러지 못해서 아쉬웠다.