
🔗
풀이
물건을 잘라서 넣을 수 없으므로 그리디처럼 풀 수는 없다. 모든 물건에 대해서 배낭에 넣거나 넣지 않거나 2가지 경우의 수가 있기 때문에 완전 탐색으로 풀게 되면 2^(물건의 개수)의 경우의 수를 가진다. 하지만 물건의 수가 100이라 불가능하다.
어떤 물건을 넣거나, 넣지 않거나 모든 경우의 수를 다 따져볼 수 없다면 매번 최적의 수를 구할 수 있는 다른 방법을 찾아야 한다. 최대 무게 K까지 모든 물건을 넣거나 넣지 않아보면서 최대 가치를 찾아나가야 한다.
최대 무게 K가 7일 때 각 물건이 아래와 같이 있다고 하자. (무게, 가치) 순이다.
1번 물건 : (6, 13)
2번 물건 : (4, 8)
3번 물건 : (3, 6)
4번 물건 : (5, 12)
1번 물건부터 배낭에 넣는다고 생각한다. 최대 무게가 7이기 때문에 1번 물건은 넣을 수 있다. 1번 물건을 넣었으므로 현재 최대값은 13이다. 만약 배낭의 무게가 6kg 미만이었다면 이 물건을 넣을 수 없었을 것이다. 만약 1번 물건을 넣지 않는다면 가치는 0이 되고 어떤 물건도 들어가있지 않게 된다. 1번 물건을 넣게 되면 무게 7에서 1번 물건의 무게인 6을 뺀 1만큼의 무게만 남게 되고, 가치의 최대값은 13이다.
2번 물건을 넣는 경우를 생각해보자. 1번 물건을 넣거나 넣지 않은 경우를 따져본 상태이기 때문에 2번 물건을 넣을 때는 1번 물건이 들어있는지 아닌지도 고려해야 한다. 6미만의 무게에는 1번 물건이 들어갈 수 없고, 2번 물건의 무게인 4이상의 경우에만 2번 물건을 넣을 수 있다. 4이상 6미만은 2번 물건만 넣을 수 있으므로 가치는 8이다. 6이상부터는 1번 물건을 넣은 경우와 비교해서 따져야 한다. 1번 물건을 넣는 것과 2번을 넣는 것 둘 중 어떤 것이 더 최대값을 가질 수 있을까? 둘 다 넣을 수 있다면 좋겠지만 1번의 무게가 6이기 때문에 최대 무게 7에서 6을 빼면 남는 공간은 1이라 불가능하다. 만약 최대 무게가 10이었다면 가능했을 것이다. 아무튼 무게 6이상에서는 둘 중 하나만 넣어야 하고 그렇다면 가치가 더 큰 것을 넣는 게 이득이므로 1번을 넣게 된다.
현재까지 1,2번 물건을 넣거나 넣지 않은 경우를 고려한 현재 상태를 표로 나타내면 아래와 같다.
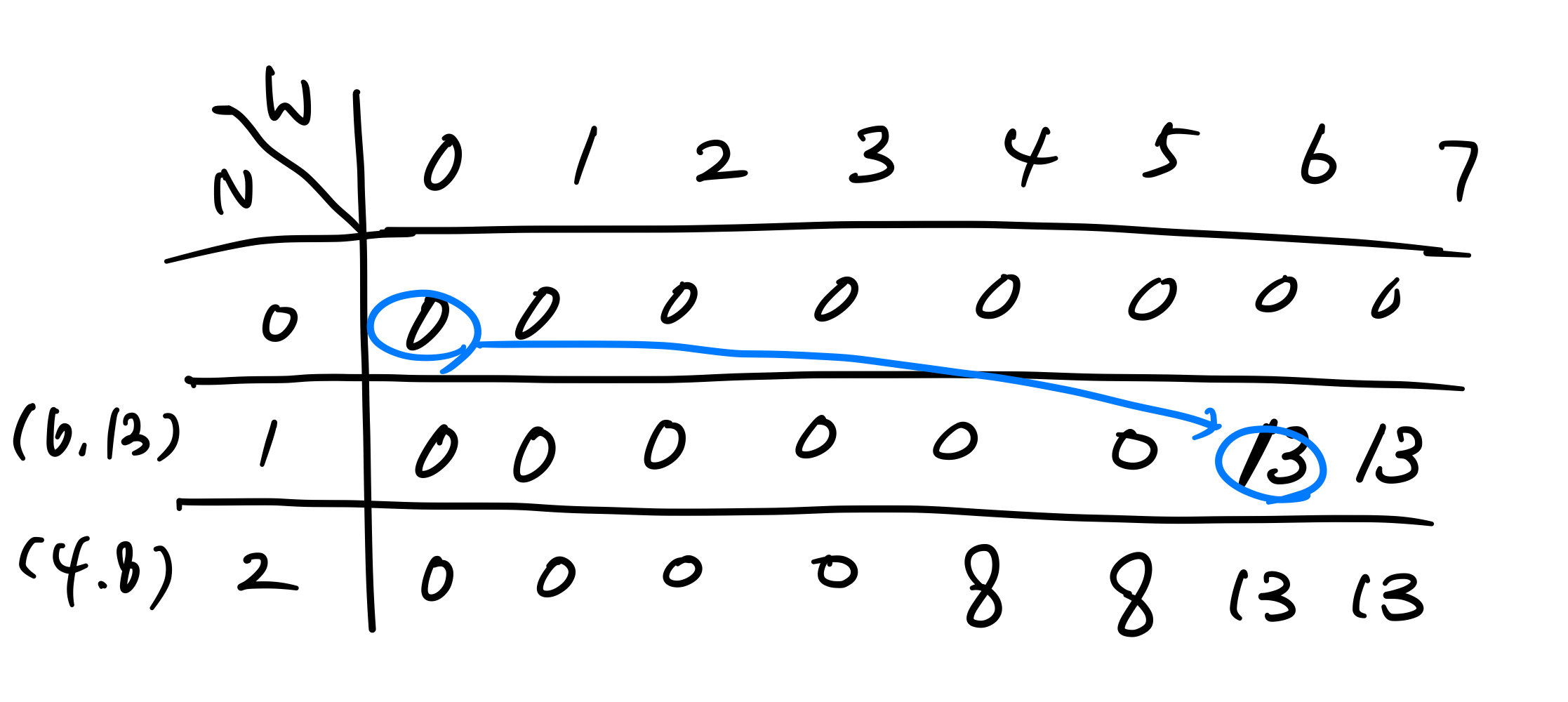
표로 표현된 2차원 배열의 이름을 dp라고 하자. dp[i][j]는 i번 물건을 넣었을 때, j개의 무게가 최대무게라고 가정했을 때 가질 수 있는 가치의 최댓값을 의미한다. 즉 2번 물건까지 넣었을 떄 최대 무게가 4라면 가질 수 있는 무게는 dp[2][4] = 8이 되는 것이다.
표를 보면 크게 3가지 경우로 나뉠 수 있다는 걸 짐작할 수 있다.
1. 최대 무게 w보다 현재 넣으려는 물건의 무게가 큰 경우
1번의 무게가 6이라서 최대 무게가 5인 경우에는 넣을 수 없던 경우를 생각하면 된다. 표에서는 1행의 5열까지, 2행의 3열까지가 여기에 해당한다. 이 경우는 현재 물건을 넣을 수 없으므로 이전 물건을 넣었을 때의 최대 값을 그대로 가져온다. 현재 물건을 넣지 않는 경우이다.
dp[i][j] = dp[i-1][j]
2. 물건을 반드시 넣는 경우
최대 무게보다 현재 물건의 무게가 적게 나가고 현재 물건을 넣는 경우이다. 가치에 음수가 없으므로 물건은 많이 넣을 수록 이득이지만 그렇다고 무조건 넣을 수는 없다.
물건을 차례대로 넣고 있기 때문에 현재 물건의 직전 물건까지 넣고 나서의 남은 무게를 계산하고 가능한지 확인해야 한다. 만약 물건을 무조건 넣으려고 한다면 현재 넣으려는 물건의 무게만큼 공간을 비워야 한다. 즉, 현재 물건의 무게만큼 뺀 다음에 거기에 현재 물건을 넣어야 한다는 개념이다
즉 현재 물건의 무게가 w이고, 최대 무게가 K라면 K-w일 때의 무게에 현재 물건을 넣어야 하는 것이다. 즉 직전 물건까지 넣었을 때 최대 무게가 K-w인 경우의 값을 가져오면 된다. 현재 물건이 i번이라면 dp[i][K] = dp[i-1][K-w] + (i번 물건의 가치) 가 된다.
dp[i][j] = dp[i-1][j-w] + (i번의 가치)
3. 물건을 반드시 넣지 않는 경우
아예 넣지 않는 경우도 존재할 수 있다. 현재 물건을 넣기 위해서는 현재 물건 만큼 무게를 빼야 하는데, 그렇게 빼고 현재 물건을 넣었을 때 가치가 하락할 수 있기 때문이다. 현재 물건을 넣지 않았다면 직전 물건을 넣었을 때의 최대 가치를 그대로 가져오면 된다.
dp[i][j] = dp[i-1][j]
현재까지 설명을 정리하면 아래와 같다.

연두색 표시는 물건의 무게가 최대 무게를 초과하는 경우이다. 이 경우는 아예 넣을 수 없다.
파란색의 경우 가방에 물건을 반드시 넣게 되는 경우이다. 최대 무게가 2이고, 물건의 무게도 2이므로 직전 행의 0번째 열에서 값을 가져와서 현재 가치를 더하면 된다.
빨간색의 경우 현재 물건을 넣는 경우와 넣지 않는 경우를 비교하게 된다. 현재 물건을 넣게 되면 dp[2-1][4-4]+6 = 6이지만 현재 물건을 넣지 않고 직전 물건만 넣은 가치를 그대로 가져오게 되면 8로 더 큰 가치를 지닌다.
하지만 무게가 6이 되었을 때인 초록색의 경우는 2번 물건을 넣었을 때 더 큰 가치를 가지게 된다. dp[2-1][6-2] = 8이기 때문이다.
종합해서 찾은 점화식은 아래와 같다.

# 평범한 배낭
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
items = [list(map(int, input().split())) for _ in range(N)]
dp = [[0]*(K+1) for _ in range(N+1)]
for i in range(1, N+1):
w, v = items[i-1]
for j in range(1, K+1):
if j < w:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j-w]+v, dp[i-1][j])
print(dp[-1][-1])