[BOJ] 1504. 특정한 최단 경로 (🥇, 다익스트라)

🔗

풀이

1 에서 N 으로 갈 때 u, v 두 개의 정점을 반드시 지나야 한다고 하는데 경로 그려보면 가능한 경우는 아래 두 가지 뿐이다.

결국 구해야 하는 최단 경로는 아래와 같다.

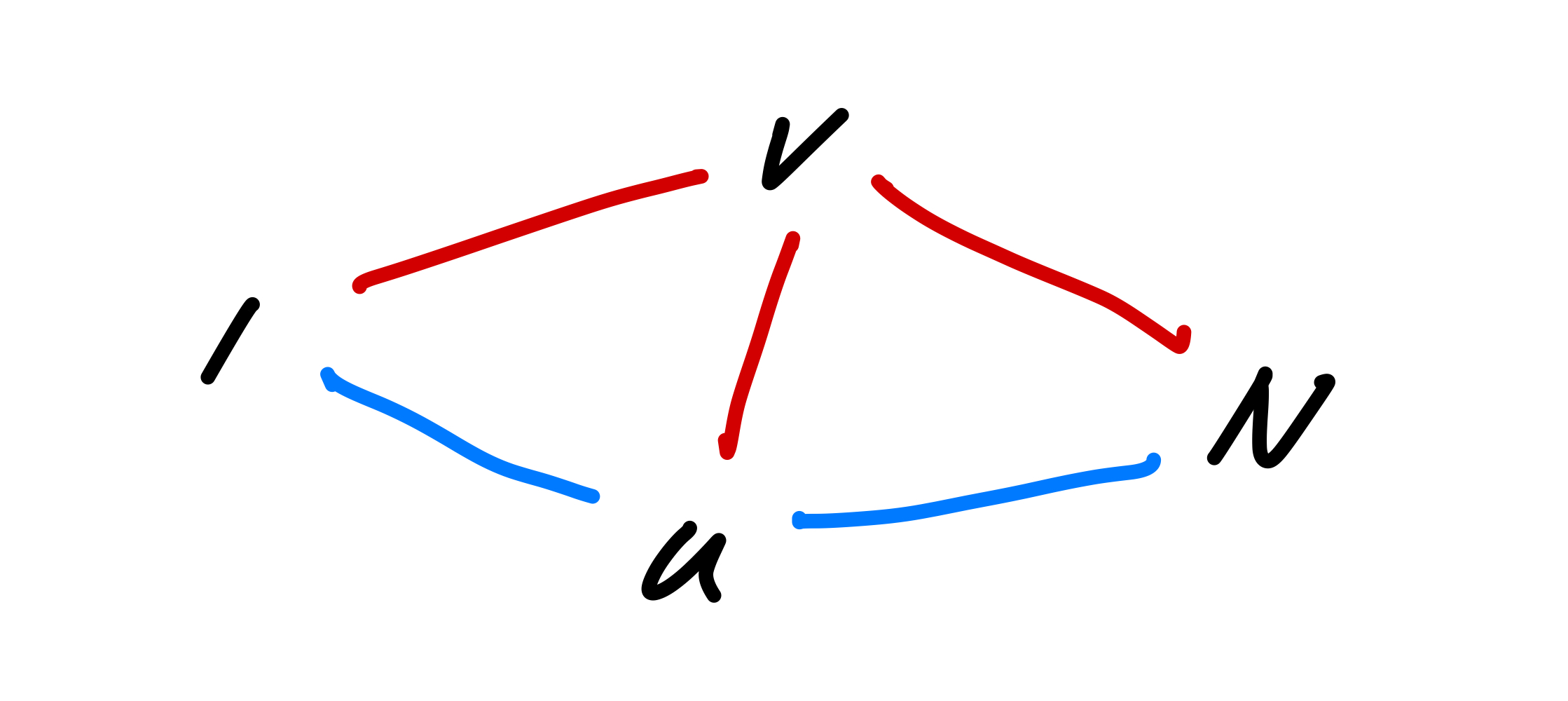
v 에서 1, u, N으로 가는 경로들과 u에서 1, v, N으로 가는 최단 경로들을 구하면 된다. 방향성이 없기 때문에 v에서 u로 가든 u에서 v로 가든 똑같다. 각 경로에 가중치가 있으므로 다익스트라를 통해 u와 v 두 개의 정점에 대해 나머지 모든 정점에 대한 최단 경로를 구한 뒤 1차원 배열 distance 형태로 반환하고 거기서 값을 찾아서 계산하면 될 것 같았다.

문제는 만약 도달할 수 없는 경우는 어떻게 구할 것이냐의 문제였다. 결국은 위의 그림에 있는 경로들 중 단 하나의 경로라도 불가능하다면 도달할 수 없게 된다. 다익스트라에서는 해당 정점에 도달하지 못하는 경우 초기화 해둔 최대값이 그대로 남아있게 되는데 만약 해당 정점에 여전히 최대값이 저장되어 있다면 해당 정점에 도달할 수 없는 것으로 판단한다.

// 특정한 최단 경로 

package Baekjoon.Gold;

import java.io.*;
import java.util.*;

public class baekjoon_1504 {
    static int N;
    static int E;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        E = Integer.parseInt(st.nextToken());

        List<List<long[]>> graph = new ArrayList<>();
        for (int i = 0; i < N+1; i++) {
            graph.add(new ArrayList<>());
        }

        for (int i = 0; i < E; i++) {
            st = new StringTokenizer(br.readLine());
            int v1 = Integer.parseInt(st.nextToken());
            int v2 = Integer.parseInt(st.nextToken());
            int c = Integer.parseInt(st.nextToken());
            graph.get(v1).add(new long[]{v2, c});
            graph.get(v2).add(new long[]{v1, c});
        }

        st = new StringTokenizer(br.readLine());
        int u = Integer.parseInt(st.nextToken());
        int v = Integer.parseInt(st.nextToken());
        long[] uDistance = shortDistance(u, graph);
        long[] vDistance = shortDistance(v, graph);


        System.out.println(solution(uDistance, vDistance, u, v));
    }

    private static long solution(long[] distance1, long[] distance2, int u, int v) {
        if (E == 0 || distance1[1] == Long.MAX_VALUE || distance1[u] == Long.MAX_VALUE || distance1[N] == Long.MAX_VALUE ||
                distance2[1] == Long.MAX_VALUE || distance2[N] == Long.MAX_VALUE) return -1;

        return Math.min(distance1[1] + distance1[v] + distance2[N], distance2[1] + distance2[u] + distance1[N]);
    }

    /**
     * 특정 정점에 대해 다른 모든 정점에 대한 최단 거리 구하기
     */
    private static long[] shortDistance(int start, List<List<long[]>> graph) {
        PriorityQueue<long[]> pQ = new PriorityQueue<>(Comparator.comparingLong(arr -> arr[1]));
        long[] distance = new long[N+1];
        Arrays.fill(distance, Long.MAX_VALUE);
        distance[start] = 0;
        pQ.add(new long[]{start, 0});

        while (!pQ.isEmpty()) {
            long[] now = pQ.poll();

            int nowNode = (int) now[0];
            if (now[1] > distance[nowNode]) continue;
            for (long[] next : graph.get(nowNode)) {
                int nextNode = (int) next[0];
                long addDistance = next[1];
                if (distance[nextNode] > now[1] + addDistance) {
                    distance[nextNode] = now[1] + addDistance;
                    pQ.add(new long[]{nextNode, distance[nextNode]});
                }
            }
        }

        return distance;
    }
}