[BOJ] 17831. 대기업 승범이네 (💎, 트리 DP)

🔗

풀이

멘토링 관계를 자료구조로 표현하면 트리 구조가 된다. 멘토는 부모 노드, 멘티는 자식 노드다. 만약 부모 노드가 하나의 자식 노드와 멘토링 관계를 맺게 되면 나머지 자식 노드들과는 멘토링 관계를 맺을 수 없다. 결국 멘토링 관계라는 건 모든 노드들에 대해서 자식 노드와 관계를 맺거나 맺지 않거나 하는 두 가지 선택지만 존재할 수 있다. 이때 한 노드가 하나의 자식 노드와 관계를 맺는 경우를 부모가 선택된 경우라고 하자. 그럼 하나의 노드가 그 어떤 자식 노드와도 관계를 맺지 않게 되는 경우도 존재할 것이다.

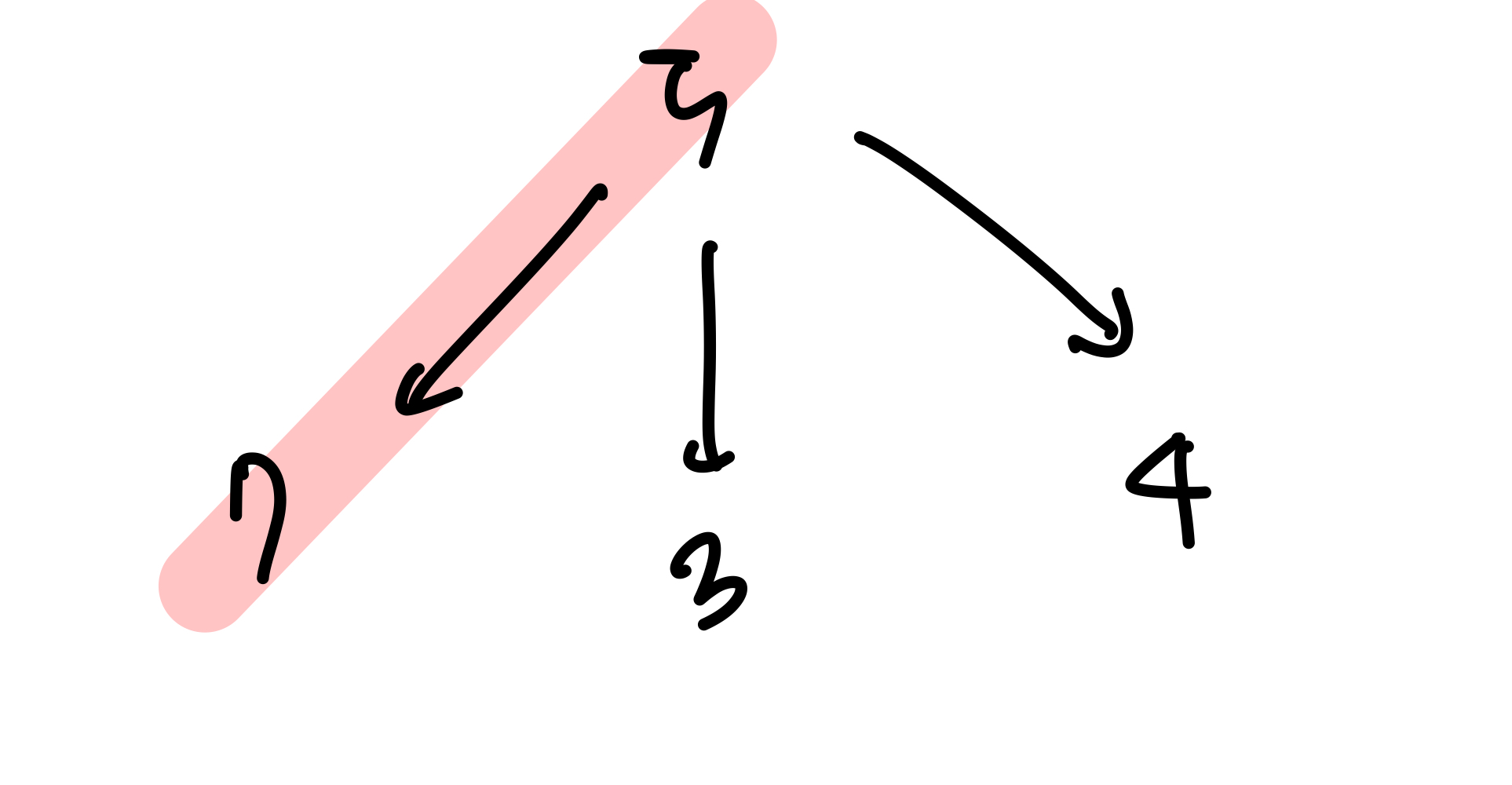
그림에서처럼 5와 7이 관계를 맺게 될 경우, 7은 자신의 자식 노드들과는 관계를 맺을 수 없다. 반면 5의 나머지 자식 노드들인 3과 4는 5와는 관계를 맺을 수 없지만 자신의 자식노드들과는 관계를 맺을 수도 있고 아닐 수도 있다. 정리하면 아래와 같다.

1. 하나의 노드가 하나의 자식 노드와 관계를 맺을 경우 해당 자식 노드는 그의 자식 노드들과 관계를 맺을 수 없다.
2. 이때 나머지 노드들은 자식 노드와 관계를 맺을 수도 있고 아닐 수도 있으며 둘 중 더 큰 경우를 택한다.

결국 dp[i][0] 은 특정 자식 노드와의 실력을 곱한 값에 특정 자식 노드가 선택되지 않은 dp[child][1] 값을 더하고, 거기에 나머지 자식 노드들이 선택되거나 or 선택되지 않은 값들 중 최대값을 더한다. dp[i][1] 은 해당 노드가 어차피 선택되지 않으므로 모든 자식 노드에 대해서 선택되거나 or 선택되지 않은 값 중 최대값들만 더하면 된다.

풀이에서는 모든 자식 노드들에 대해서 선택되거나 or 선택되지 않은 값을 totalSum으로 미리 구하고, 특정 자식 노드들을 선택한 경우 만약 해당 노드가 자식 노드와 관계를 맺을 경우가 아닌 경우보다 큰 값이라면 totalSum에 값이 더해져 있을 것이므로 제외하고, 자식 노드와 관계를 맺지 않은 경우에 대한 값을 더해서 보정한 후 해당 자식 노드와 부모의 실력을 곱한 값을 더하는 방식으로 구했다.

탐색은 1번 노드에서 시작하여 리프 노드까지 도달한 후 다시 역으로 1번 노드까지 되돌아올 수 있도록 하기 위해 깊이 우선 탐색을 사용했다.

import java.util.*;
import java.io.*;

public class Main {
    static List<List<Integer>> tree = new ArrayList<>();
    static int[] talent;
    static void dfs(int cur, long[][] dp) {
        if (tree.get(cur).size() == 0) {
            return;
        }

        int totalSum = 0;
        for (int child : tree.get(cur)) {
            dfs(child, dp);
            totalSum += Math.max(dp[child][0], dp[child][1]);
        }
        dp[cur][1] += totalSum;

        for (int selectChild : tree.get(cur)) {
            if (dp[selectChild][0] > dp[selectChild][1]) {
                dp[cur][0] = Math.max(dp[cur][0], (totalSum - dp[selectChild][0]) + dp[selectChild][1] + talent[selectChild] * talent[cur]);
            } else {
                dp[cur][0] = Math.max(dp[cur][0], totalSum + talent[selectChild] * talent[cur]);
            }
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        for (int i = 0; i < N; i++) {
            tree.add(new ArrayList<>());
        }
        
        int par;
        StringTokenizer st = new StringTokenizer(br.readLine());
        for (int i = 1; i < N; i++) {
            par = Integer.parseInt(st.nextToken());
            tree.get(par-1).add(i);
        }

        talent = new int[N];
        st = new StringTokenizer(br.readLine());
        for (int i = 0; i < N; i++) {
            talent[i] = Integer.parseInt(st.nextToken());
        }
        
        long[][] dp = new long[N][2];
        dfs(0, dp);
        // for (int i = 0; i < dp.length; i++) {
        //     System.out.println(Arrays.toString(dp[i]));
        // }

        System.out.println(Math.max(dp[0][0], dp[0][1]));
    }
}