[BOJ] 1937. 욕심쟁이 판다 (🥇, DP/DFS)

🔗

풀이

예제에서 이동할 수 있는 최대 경로의 길이는 4이고 가능한 경로는 위의 3가지이다.

단순하게 모든 칸을 다 순회하면서 최대 경로를 찾는 방법도 가능하겠지만 최대 칸 수가 2만이 넘기 때문에 모든 칸에 대해 브루트포스로 찾는 것은 불가능하다.

대신 한 번 방문한 칸에 대해서는 그 칸에서 출발했을 때 최대 경로의 길이가 얼마나 가능한지는 알아낼 수 있다. 즉, 한 점에서 출발해서 가능한 모든 경로를 탐색하면서 모든 경로들에 대해서 해당 위치에서 출발했을 때 가능한 최대 경로들을 구해두는 것이다. 그래서 다음 번에 그 경로를 다시 방문해야 할 일이 생겼을 때는 그 최대 경로의 값을 가져와서 더해주기만 하면 된다.

1. 해당 위치에서 출발해 가능한 모든 곳 dfs 탐색
2. 한 번 탐색된 곳은 해당 위치에 대한 가능한 최대 경로 길이에 대해 저장
3. 최대 경로 길이가 저장된 곳에 대해서는 재탐색X

그림에서 보면 1 -> 7 -> 15로 이동하는 경로가 가능하다. 그런데 15에서는 주변에 자신보다 더 높은 값을 가지는 칸이 없기 때문에 어느곳으로도 이동이 불가능하다. 그래서 자신의 값에 1을 저장하고 이 값을 반환하게 된다. 그러면 15로 이동하기 전의 칸이었던 7로 되돌아오게 되고 7은 반환받은 값 1에다가 +1을 해주고(7에서 15로 한 칸 더 이동했었기 때문에) 이 값을 다시 반환하게 된다. 이런식으로 깊이 우선 탐색을 수행하면서 반환받은 값에 +1을 더한 값을 더해서 최대 경로를 구하는 것이 기본적인 풀이 방법이다.

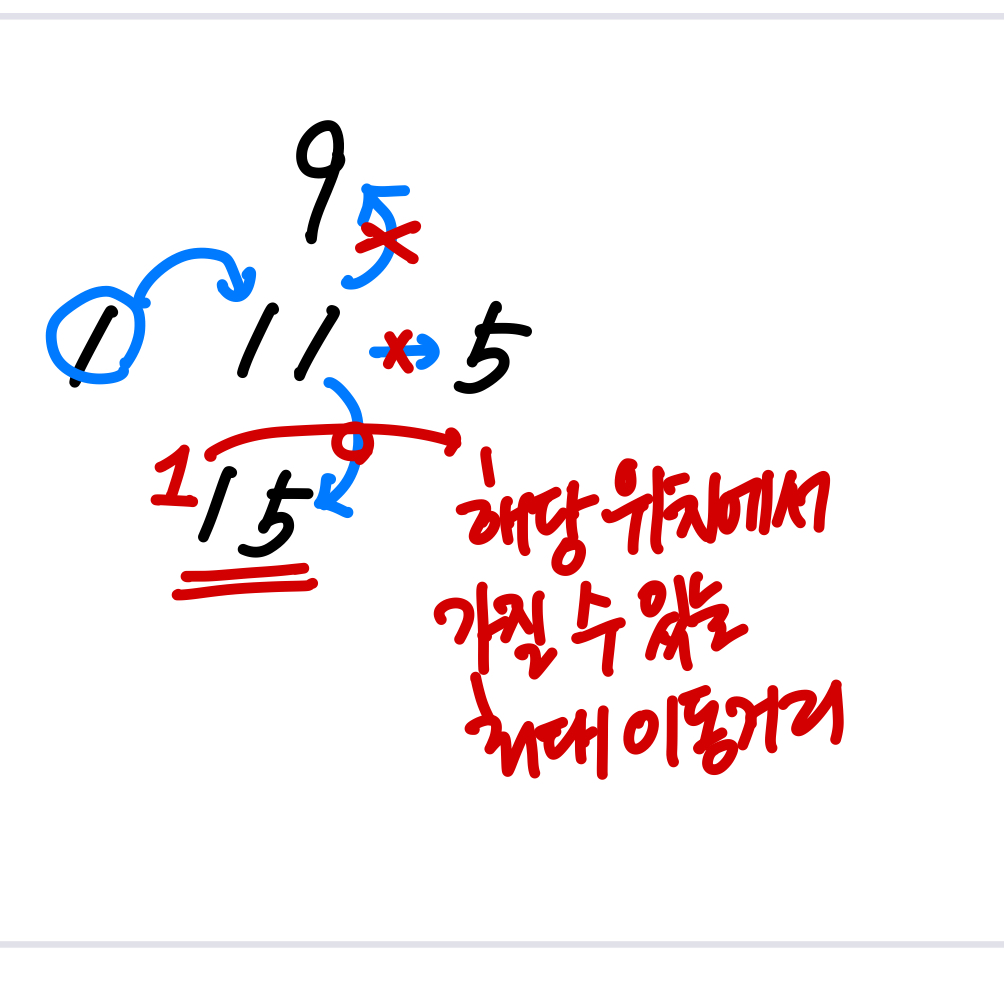
여기에 DP 개념을 추가해주게 되는데, 그림을 보면 1에서 11로 이동하게 되면 15로 다시 이동할 수 있다. 하지만 위에서 이미 15에서 얻을 수 있는 최대 경로 길이(1)을 구해놨기 때문에 이런 경우에는 굳이 15로 이동할 필요 없이 그 값만 가져와서 더해주면 된다.

1. 이동하려는 칸이 최대 경로 값을 이미 갖고 있다면 가져와서 더해줄 것
2. 갖고 있지 않다면 dfs 탐색

위의 2가지 방법을 상, 하, 좌, 우 칸에 대해 모두 반복하고 반복한 값들 가운데 가장 큰 값을 저장해서 매번 반환하면 된다.

파이썬으로 풀이했고 최대 재귀 탐색 깊이가 999이기 때문에 25001으로 늘려주었다. 추가적으로 작은 칸의 값부터 시작하면 좀 더 유리할 것이라 생각해서 우선순위큐에 칸의 값이 작은 순서대로 담아서 문제를 풀이했는데 그닥 유리했던 것 같진 않다. (0, 0)부터 차례대로 풀이해도 가능할듯.

# 욕심쟁이 판다

import heapq, sys
sys.setrecursionlimit(25001)

def dfs(i, j):
    for ni, nj in (i-1, j), (i+1, j), (i, j-1), (i, j+1):
        if ni < 0 or nj < 0 or ni >= n or nj >= n or forest[ni][nj] <= forest[i][j]:
            continue

        if dist[ni][nj]:
            dist[i][j] = max(dist[i][j], dist[ni][nj]+1)
        else:
            dist[i][j] = max(dist[i][j], dfs(ni, nj))
    return dist[i][j]+1


n = int(input())
forest = [list(map(int, input().split())) for _ in range(n)]
dist = [[0] * n for _ in range(n) ]
pq = []

for i in range(n):
    for j in range(n):
        heapq.heappush(pq, (forest[i][j], i, j))

while pq:
    x, i, j = heapq.heappop(pq)
    if dist[i][j]:
        continue
    dist[i][j] = max(1, dfs(i, j))

answer = 0
for row in dist:
    answer = max(answer, max(row))

print(answer)