[BOJ] 21923. 곡예 비행 (✈️, DP)

🔗

풀이

전체 배열의 크기가 1000x1000으로 백만이기 때문에 브루트포스 방식으로 모든 경우의 수를 탐색하는 건 불가능하고 한 번의 탐색으로 최대값을 구할 수 있어야 하므로 다이나믹 프로그래밍을 사용했다.

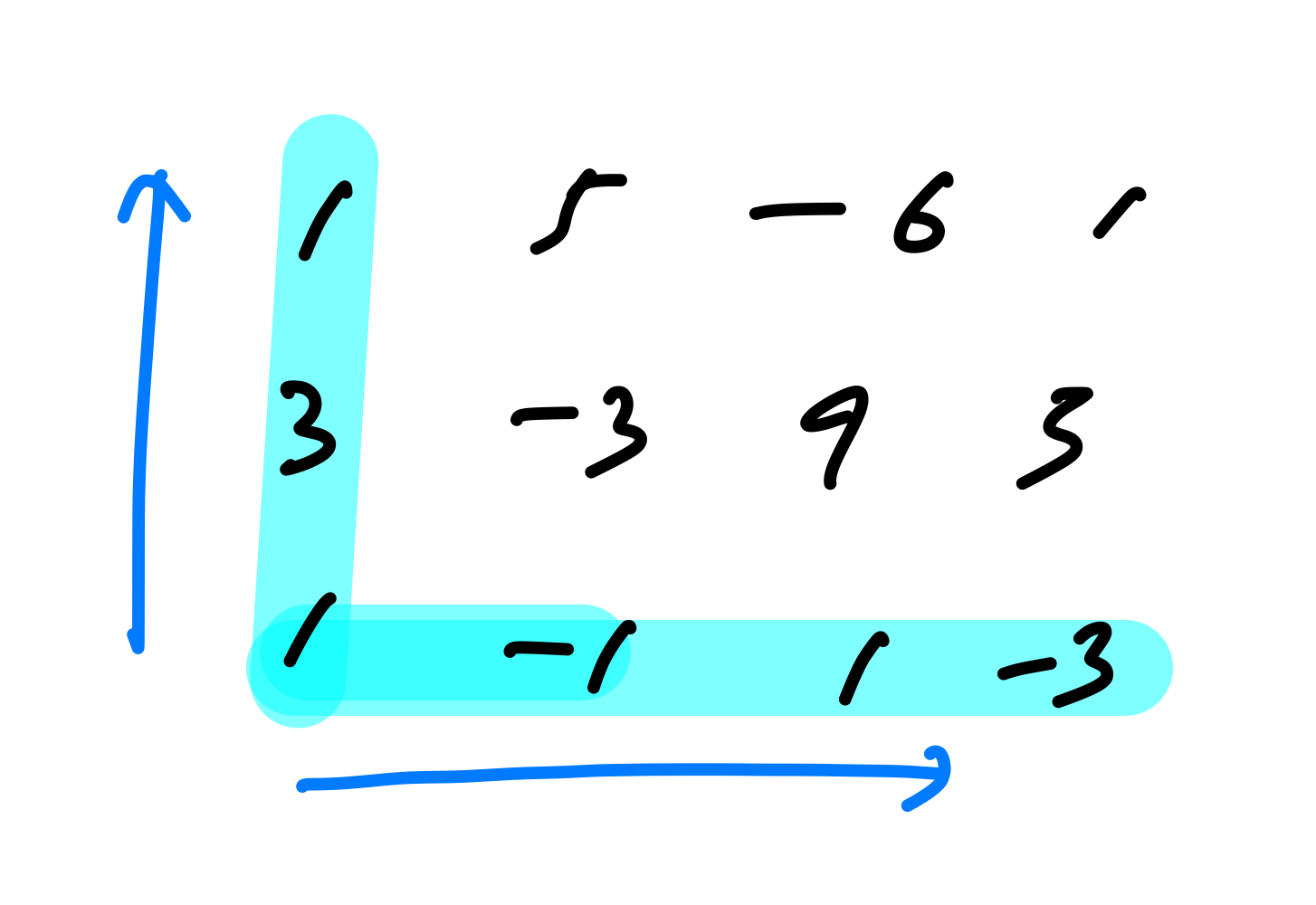
우선 상승의 경우 위와 오른쪽으로만 갈 수 있다고 하였고 시작점은 반드시 좌측 하단이여야 한다. 즉, 파란색 경로는 무조건 위로 올라오는 방식과 무조건 오른쪽으로 이동해서 도착하는 방법 외에는 없다는 뜻이 된다.

해당 경로의 점수를 누적해서 구하면 위와 같다.

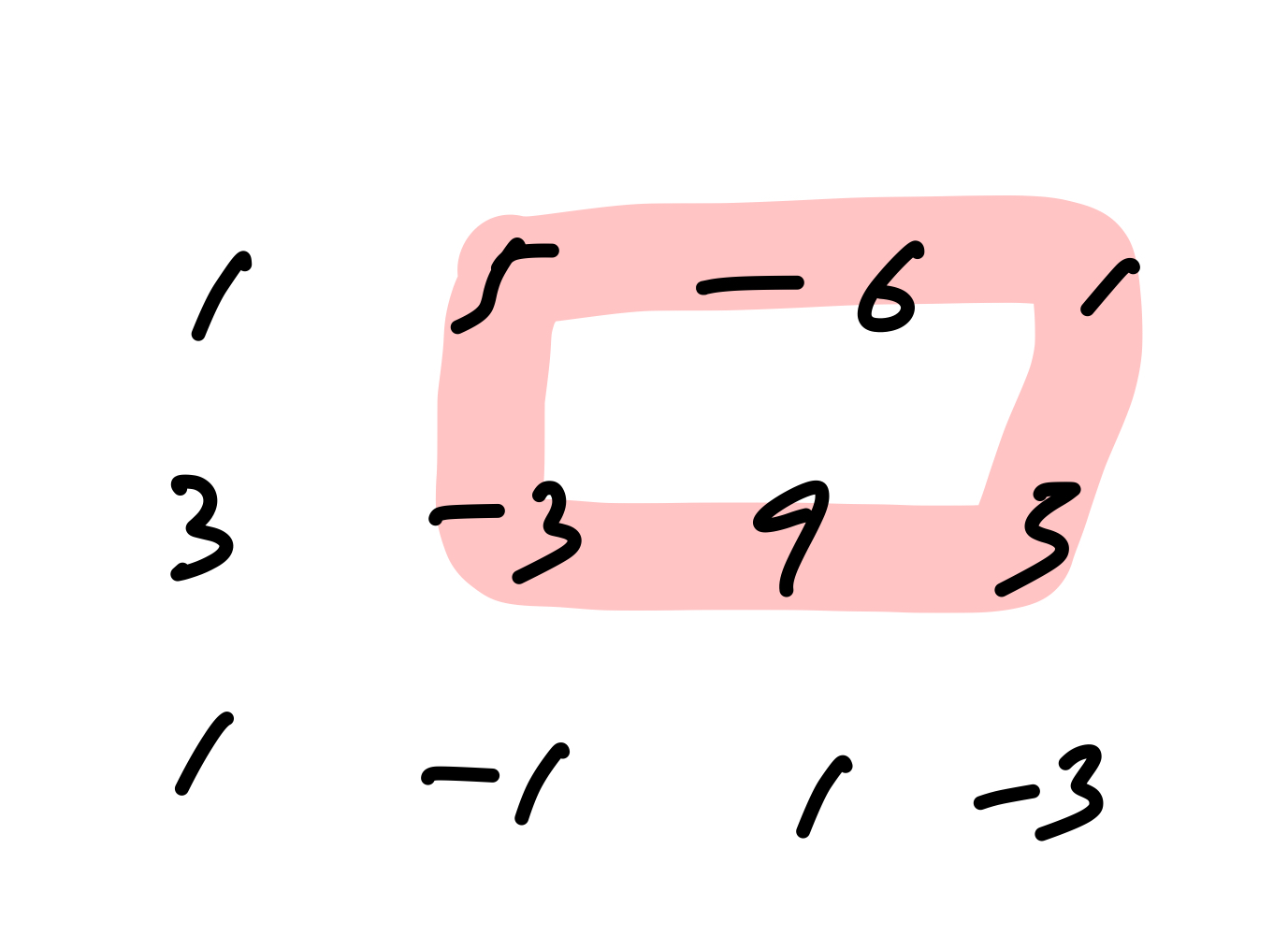
이제 나머지에 해당하는 분홍색 경로의 점수를 구해야 한다.

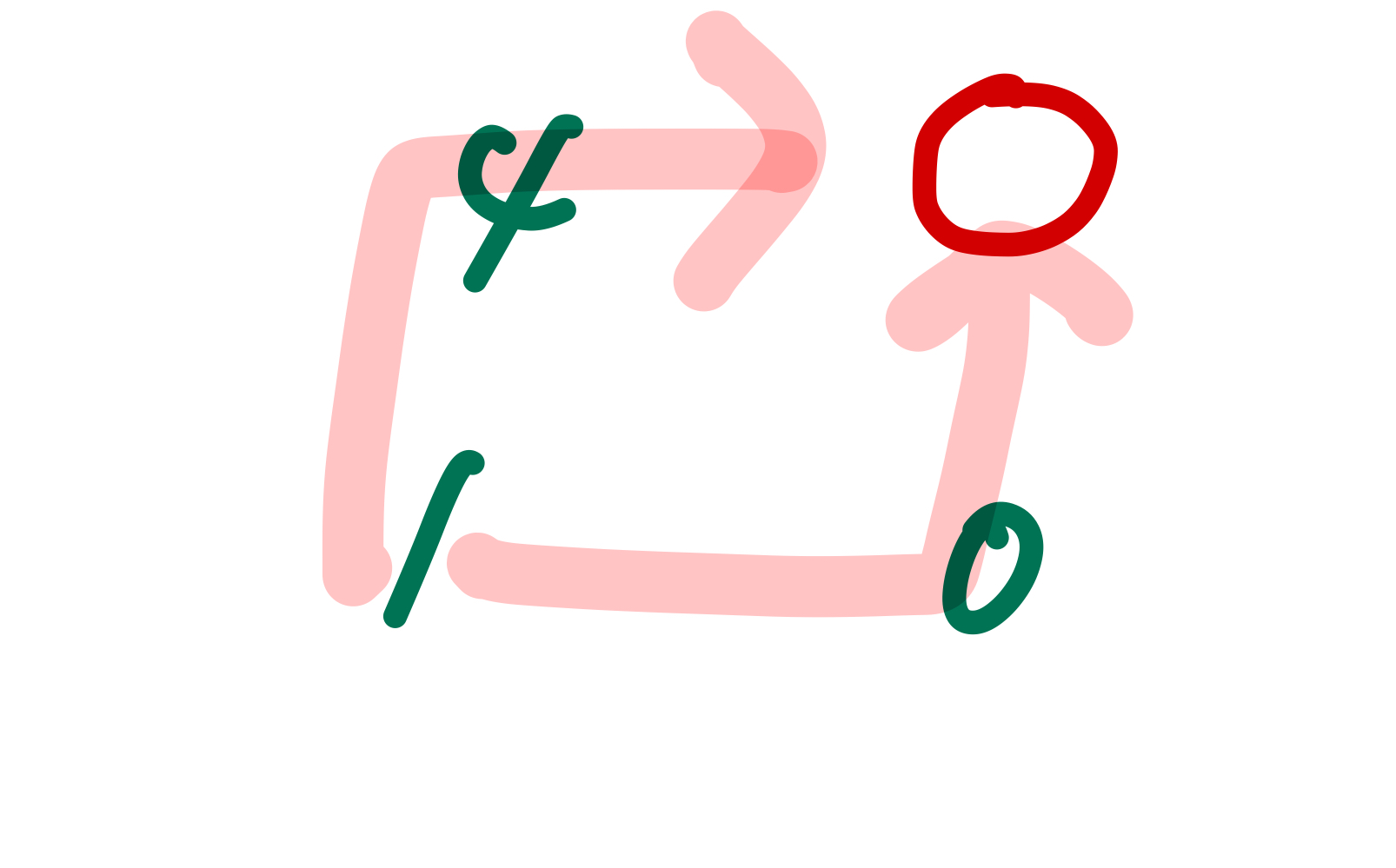
그런데 해당 경로들에 도달할 수 있는 방법은 단 2가지이다. 아래에서 올라오는 방법과 왼쪽에서 이동해서 도착하는 방법 뿐이다. 위에서 언급했듯 상승 비행의 경우 반드시 오른쪽 아니면 위로 이동하는 방법밖에 없다고 했기 때문이다. 모든 경로는 한 칸씩 누적해서 이동하도록 되어 있으므로 왼쪽이나 아래쪽 중에서 점수가 더 큰 쪽의 경로를 택해서 점수를 누적해나가면 된다.

하강 비행은 우측 아래쪽을 기준으로 상승 비행과 같은 방식으로 구하면 된다. 원래대로라면 하강 비행은 특정 점에서 오른쪽 아래로만 이동해서 우측 아래로 오는 것이지만 반대로 우측 아래에서 위, 왼쪽으로만 이동할 수 있다고 가정해도 같은 방식으로 해결할 수 있다.

하강 비행은 상승 비행이 끝난 위치에서 시작한다고 하였으므로 상승 위 그림처럼 상승 비행과 하강 비행의 경우 얻을 수 있는 각 위치의 점수를 모두 구한 후 전체 좌표를 탐색하며 (상승 비행의 점수 + 하강 비행의 점수)가 가장 높은 것을 선택하면 된다.

import java.util.*;
import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int[][] arr = new int[N][M];
        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 0; j < M; j++) {
                arr[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        int[][] upLeft = new int[N][M];
        upLeft[N-1][0] = arr[N-1][0];
        for (int i = 1; i < M; i++) {
            upLeft[N-1][i] += upLeft[N-1][i-1] + arr[N-1][i];
        }   

        for (int i = N-2; i > -1; i--) {
            upLeft[i][0] += upLeft[i+1][0] + arr[i][0];
        }

        for (int i = N-2; i > -1; i--) {
            for (int j = 1; j < M; j++) {
                upLeft[i][j] = Math.max(upLeft[i+1][j], upLeft[i][j-1]) + arr[i][j];
            }
        }

        int[][] rightDown = new int[N][M];
        rightDown[N-1][M-1] = arr[N-1][M-1];
        for (int j = M-2; j > -1; j--) {
            rightDown[N-1][j] += rightDown[N-1][j+1] + arr[N-1][j];
        }

        for (int i = N-2; i > -1; i--) {
            rightDown[i][M-1] += rightDown[i+1][M-1] + arr[i][M-1];
        }

        for (int i = N-2; i > -1; i--) {
            for (int j = M-2; j > -1; j--) {
                rightDown[i][j] = Math.max(rightDown[i+1][j], rightDown[i][j+1]) + arr[i][j];
            }
        }
        
        long answer = Long.MIN_VALUE;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                answer = Math.max(answer, upLeft[i][j] + rightDown[i][j]);
            }
        }

        System.out.println(answer);
    }
}