[BOJ] 2696. 중앙값 구하기 (🥇, 우선순위 큐)

🔗

풀이

수열의 최대 크기는 9999이기 때문에 매번 숫자가 추가될 때마다 정렬을 하고 중앙값을 찾는 방식은 비효율적이다.

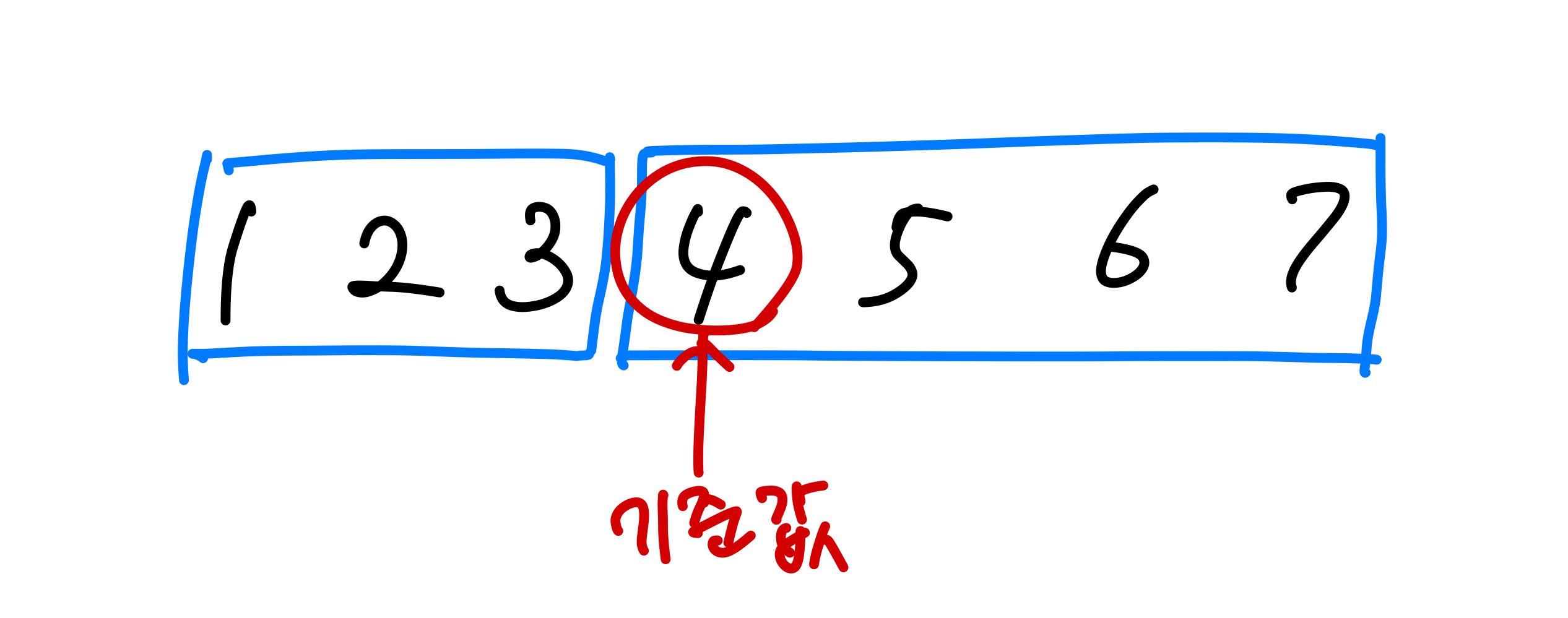
어떤 수열을 정렬해서 중앙값을 찾을 때의 구조는 위와 같다. 길이는 항상 홀수이기 때문에 중앙값을 기준으로 더 작은 값과 중앙값을 포함한 더 큰 값들로 나누면 항상 더 큰 값들을 가진 쪽의 개수가 1개 더 많게 된다.

매번 추가 되는 값에 대해서 정렬을 하거나 해다 값이 속할 위치를 찾는 방식은 시간복잡도가 걸리기 때문에 우선순위 큐를 사용한다. 기준값보다 작은 값들에 대해서는 lowQ를, 기준값보다 큰 값들에 대해서는 highQ에 추가하는 방식이다.

그러나 이런 식의 방식이 항상 lowQ의 길이를 highQ의 길이보다 1만큼 작게 해주지는 않기 때문에 홀수번째가 되어서 기준값을 출력해야 될 때가 되면 lowQ의 길이가 highQ의 길이보다 1만큼 작도록 조정하는 과정을 거친다.

이때 lowQ의 길이가 더 길다면 highQ로 값을 옮겨서 길이를 맞춰야 하는데 그러기 위해서는 lowQ에서 최대값들을 먼저 highQ로 옮겨야 수열의 순서를 유지할 수 있다. 그래서 lowQ에 어떤 값을 추가하거나 highQ로 어떤 값을 옮길때는 항상 음수로 변환한다.

import java.util.*;
import java.io.*;

public class Main {
    static final int LIMIT_NUMBER = 10;
    
    static int[] solution(int M, int[] arr) {
        Queue<Integer> lowQ = new PriorityQueue<>();
        Queue<Integer> highQ = new PriorityQueue<>();
        highQ.add(arr[0]);
        
        int[] answer = new int[(M+1)/2];
        answer[0] = arr[0];
        for (int i = 1; i < M; i++) {
            if (arr[i] >= highQ.peek()) {
                highQ.add(arr[i]);
            } else {
                lowQ.add(-arr[i]);
            }

            if (i % 2 == 1) continue; // 짝수면 지나감

            while (highQ.size() != (lowQ.size() + 1)) {
                if (highQ.size() > lowQ.size()) {
                    lowQ.add(-highQ.poll());
                } else {
                    highQ.add(-lowQ.poll());
                }
            }

            answer[i/2] = highQ.peek();
        }

        return answer;
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int T = Integer.parseInt(br.readLine());
        
        int M;
        int[] arr;
        StringTokenizer st;
        while (T-- > 0) {
            M = Integer.parseInt(br.readLine());
            arr = new int[M];
            int row = 0;
            while (M > 0) {
                st = new StringTokenizer(br.readLine());
                for (int col = 0; col < Math.min(M, 10); col++) {
                    arr[10 * row + col] = Integer.parseInt(st.nextToken());
                }
                M -= 10;
                row++;
            }

            int[] answer = solution(arr.length, arr);
            System.out.println(answer.length);
            StringBuilder sb = new StringBuilder();
            for (int i = 0; i < answer.length; i++) {
                sb.append(answer[i] + " ");
                if ((i+1) % 10 == 0) sb.append("\n");
            }
            System.out.println(sb);
        }
    }
}