[LeetCode] 687. Longest Univalue Path

🔗

풀이

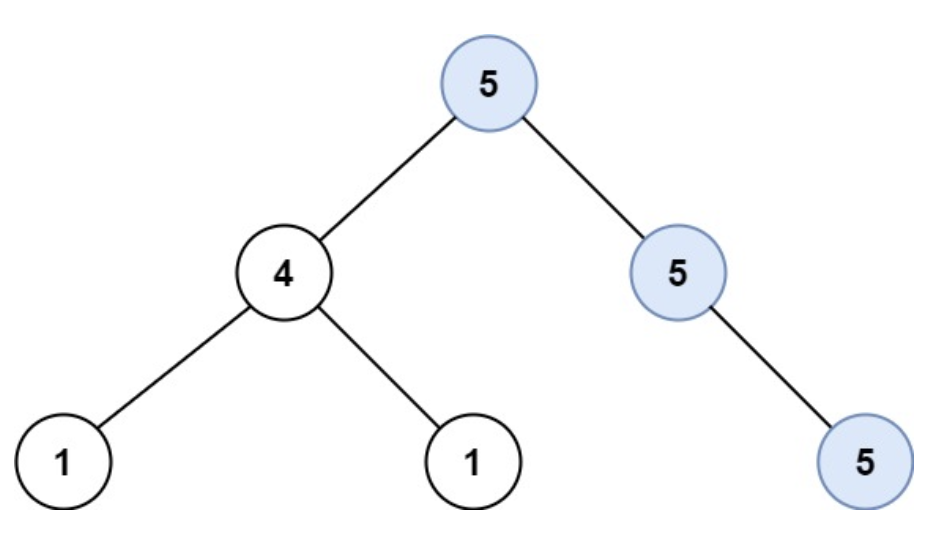
같은 값을 갖고 이어지는 가장 긴 경로를 찾는 문제이다. dfs로 트리의 리프 노드까지 도달한 후 다시 되돌아나오면서 같은 값을 가지는지 확인하고 각각의 노드마다 가질 수 있는 최대 경로의 길이를 비교하여 저장한다.

특정 노드는 왼쪽, 오른쪽 자식에서 이어져오는 경로를 둘 다 가질 수 있지만 그 노드의 부모 노드는 그 특정 노드의 왼쪽, 오른쪽 자식 중 한 가지의 경로만 가질 수 있다. 이는 특정 노드에서는 왼쪽 + 오른쪽 경로를 더한 값의 최대값을 구해야 하지만, 그 부모 노드에 반환해야 하는 값은 왼쪽, 오른쪽 경로 중 더 큰 값 하나만 반환해야 한다는 뜻이 된다.

무조건 리프 노드까지 이동해서 각 노드마다 한 번씩 재귀 탐색하는 과정을 거쳐야 하기 때문에 노드가 존재하지 않는 경우 0을 반환한다. 각 리프노드는 양쪽의 자식이 모두 없기 때문에 왼쪽과 오른쪽의 값이 모두 0이 되고, 경로 자체가 존재하지 않으므로 가질 수 있는 최대 경로의 길이는 0, 부모 노드로 반환하는 왼쪽 or 오른쪽 최대값 경로의 길이도 0이 된다.

리프 노드가 아닌 노드의 경우 자식 노드와 자신의 값이 같다면 길이는 1이 추가 되어야 한다. (5-5의 경우) 같지 않다면 이어지는 경로가 아니기 때문에 0으로 초기화 한다. (4-1의 경우)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    ans: int = 0
    def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:

        def dfs(cur):
        	# 노드가 존재하지 않으면 0 반환
            if cur is None:
                return 0
            
            # 모든 노드에 대해 탐색 진행
            left = dfs(cur.left)
            right = dfs(cur.right)
            
            # 왼쪽 자식이 존재하고 현재 노드와 값이 같으면 경로 1추가
            if cur.left and cur.left.val == cur.val:
                left += 1
            else:
                left = 0
            
            # 오른쪽 자식이 존재하고 현재 노드와 값이 같으면 경로 1추가
            if cur.right and cur.right.val == cur.val:
                right += 1
            else:
                right = 0
			
            # 현재 노드에서는 왼쪽, 오른쪽 자식의 경로를 합한 값이 최대값
            self.ans = max(self.ans, left+right)
            
            # 반환해야 하는 값은 왼, 오른쪽 경로 중 최대 경로만
            return max(left, right)
                        
        dfs(root)
        return self.ans