
최소 신장 트리
신장 트리(Spanning Tree)
신장 트리란 (1) 모든 정점을 연결하는 (2)사이클을 이루지 않는 트리이다. 하나의 연결된 그래프에 신장 트리는 반드시 한 개 이상 존재할 수 있다.
최소 신장 트리 or 최소 스패닝 트리
가중치를 가지는 무방향 간선(edge)그래프가 존재할 때 최소의 간선 비용을 가지는 신장 트리를 말한다. 구현할 때 일반적으로 크루스칼 알고리즘과 프림 알고리즘이 사용되며 두 알고리즘은 모두 현재 상황에서 최적의 선택을 하며 나아가기 때문에 그리디 알고리즘으로 분류된다.
모든 간선을 사용하지 않으면서 모든 정점을 최소 비용(또는 거리)로 연결할 수 있다는 점에서 네트워크 연결, 전선망 연결, 배수로 연결 등의 다양한 실생활 문제에서 활용될 수 있다.
코드 구현
백준의 🥇 1197. 최소 스패닝 트리 문제를 통해 크루스칼 알고리즘과 프림 알고리즘을 구현한다.
🚲 크루스칼 알고리즘(Kruskal Algorithm)
신장 트리의 특징인 사이클을 이루지 않는다는 점을 이용한 알고리즘이다. 사이클 판별은 분리 집합(Disjoint set) 자료 구조를 통해 확인하게 된다.
- 모든 간선을 비용 기준으로 오름차순정렬 한다.
- 차례대로 두 정점의 대표 노드를 확인하는 연산(
find)을 통해 사이클 여부를 판별한다.
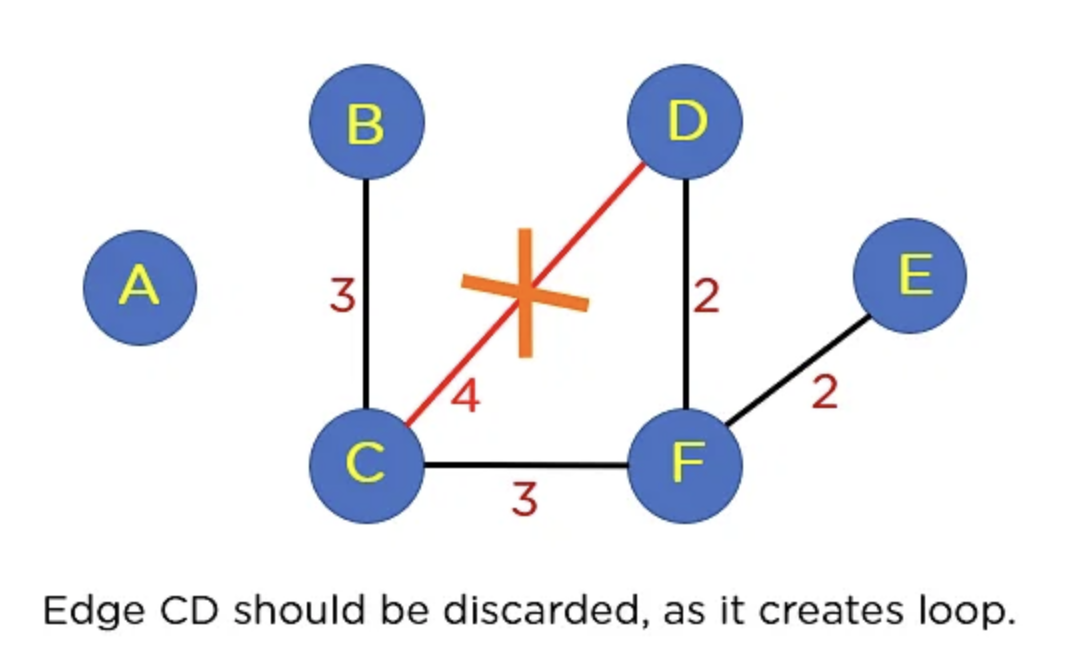
2-1. 사이클을 이루지 않는다면 두 정점을 연결한다.
2-2. 사이클을 이룬다면 이 간선은 무시한다.
초기값
여기서는 모든 간선들에 대한 정보가 저장되어야 한다. 양 정점과 비용만 저장할 수 있으면 될 것 같다. 각 정점에서 어떤 정점으로 연결되는지는 저장할 필요 없다.
대표 노드의 정보를 저장할 배열 parent가 필요하다. 초기에는 각 정점의 번호를 대표 노드 값으로 갖는다.
# 정점, 간선의 개수
V, E = map(int, input().split())
# 모든 간선에 대한 정보 입력받기
edges = [list(map(int, input().split())) for _ in range(E)]
# 각 정점에 대한 대표 노드
parent = list(range(V+1))
분리 집합 연산
크루스칼 알고리즘의 근간이 되는 분리 집합 연산 find와 union을 구현해야 한다.
정점의 개수가 1만개이기 때문에 find 연산은 최악의 경우 O(N) = 1만번의 연산을 수행하게 될 수 있다. 경로 압축을 통해 이를 줄이기로 한다.
def find(v):
if parent[v] != v: # 루트 노드가 아니라면
parent[v] = find(parent[v]) # 경로 압축(대표 노드에 부모 노드가 아니라 루트 노드를 바로 저장)
return parent[v]
def union(a, b):
a = find(a)
b = find(b)
if a < b: # 루트 노드의 수가 더 작은 쪽으로 합한다
parent[b] = a
else:
parent[a] = b사이클 여부 확인
모든 간선을 탐색하며 현재 간선을 연결하면 사이클이 형성되는지 확인한다. 사이클이 형성되는 경우는 건너뛰고 형성되지 않는 경우만 두 간선을 연결하고 비용을 합산한다.
# 비용을 기준으로 간선 정렬
edges.sort(key=lambda x: x[2])
def kruskal():
cost = 0
for a, b, c in edges:
# 사이클을 형성하지 않는다면 연결하고 비용 합산
if find(a) != find(b):
union(a, b)
cost += c
# 비용만 반환
return cost전체 코드
Pypy3: 428ms
Python3: 4192ms
def find(v):
if parent[v] != v: # 루트 노드가 아니라면
parent[v] = find(parent[v]) # 경로 압축(대표 노드에 부모 노드가 아니라 루트 노드를 바로 저장)
return parent[v]
def union(a, b):
a = find(a)
b = find(b)
if a < b: # 루트 노드의 수가 더 작은 쪽으로 합한다
parent[b] = a
else:
parent[a] = b
# 정점, 간선의 개수
V, E = map(int, input().split())
# 모든 간선에 대한 정보 입력받기
edges = [list(map(int, input().split())) for _ in range(E)]
parent = list(range(V+1))
edges.sort(key=lambda x: x[2])
def kruskal():
cost = cnt = 0
for a, b, c in edges:
print(a, b, parent)
if find(a) != find(b):
union(a, b)
cost += c
cnt += 1
if cnt == V-1:
break
return cost
print(kruskal())성능 향상
최소 신장 트리의 간선 개수는 정점 개수-1 개이다. 모든 간선을 다 훑어볼 필요 없이 최소 신장 트리를 이루는 간선을 다 찾았다고 판단되면 종료한다.
☕️ 프림 알고리즘 (Prim's Algorithm)
임의의 정점을 시작으로 최소 비용을 가지는 간선을 선택해나가는 알고리즘이다. 기본적으로 (1) 최소 신장 트리에 포함된 정점의 집합과 (2) 최소 신장 트리에 포함되지 않은 정점의 집합 2개가 서로소 집합으로 존재하게 된다. (1)의 정점들에서 (2)의 정점들과 연결된 간선 중 최소 비용을 선택해나가는 것이다.
- 임의의 정점을 선택한다.
- 그 정점 A와 그 정점에 포함되지 않은 정점들을 연결하는 간선들 중 최소 비용을 갖는 간선을 찾는다
- 찾은 간선이 A와 B를 연결하는 간선이라고 했을 때, MST에 포함되지 않는 정점 B를 MST에 추가하고 비용을 합산한다.
- 모든 정점을 찾을 때까지 2~3 과정을 반복한다.
프림 알고리즘은 배열과 우선순위 큐 두 가지로 모두 구현할 수 있다. 우선 배열로 구현한 다음 우선순위 큐로 개선하는 코드를 작성해볼 것이다.
초기값
크루스칼이 간선 중심이었다면 프림은 정점 중심이다. 각 정점들이 MST에 포함이 되는지, 각 정점들이 어떤 정점과 연결되어 있는지에 대한 정보를 저장해야 한다. 인접 리스트로 구현해도 되고 인접 행렬로 구현해도 된다.
각 정점들이 MST에 포함되어있는지를 저장하는 배열과 각 정점에 도착하는 비용들을 저장하는 cost 배열을 선언한다.
V, E = map(int, input().split())
# 각 정점에 대한 정보는 인접리스트로 저장
adjList = [[] for _ in range(V+1)]
# 무방향 = 양방향이므로 양쪽 정점에 모두 저장
for _ in range(E):
a, b, c = map(int, input().split())
adjList[a].append((b, c))
adjList[b].append((a, c))
MST = [False]*(V+1) # 최소신장트리(MST)에 현재 포함되어있는지 여부
cost = [1e13]*(V+1) # 각 정점에 연결되는 간선의 비용배열을 이용한 최소 간선 찾기
Python3에서는 시간 초과가 발생했다. 정점의 수(V)만큼 계속 반복하기 때문에 기본적으로 O(V^2)이다.
def prim(v): # v: 시작 정점
cost[v] = 0 # 출발지는 0
# 모든 정점의 횟수만큼 탐색해야 함
for _ in range(V):
# 현재 정점에서 이동할 가장 최소 간선을 찾아야 함!
u, min_cost = -1, 1e13
for i in range(V+1):
# 아직 MST에 포함되어 있지 않은 최소 비용 간선 선택
if not MST[i] and cost[i] < min_cost:
min_cost = cost[i]
u = i
MST[u] = True
# 선택된 정점을 기준으로 모든 간선 비용 업데이트(cost)
for x, w in adjList[u]:
if not MST[x] and cost[x] > w:
cost[x] = w
return sum(cost[1:])우선순위큐를 이용한 최소 간선 찾기
def prim(v):
MST = [False]*(V+1)
pq, cost = [], 0
# 간선에 대한 정보 저장 (비용, 도착 정점)
heappush(pq, (0, v))
while pq:
c, v = heappop(pq)
if MST[v]: # 이미 MST에 포함되어 있는 간선이면
continue
cost += c
for x, w in adjList[v]:
heappush(pq, (w, x))
return cost최종 코드
# 배열 사용
V, E = map(int, input().split())
# 각 정점에 대한 정보는 인접리스트로 저장
adjList = [[] for _ in range(V+1)]
# 무방향 = 양방향이므로 양쪽 정점에 모두 저장
for _ in range(E):
a, b, c = map(int, input().split())
adjList[a].append((b, c))
adjList[b].append((a, c))
MST = [False]*(V+1) # 최소신장트리(MST)에 현재 포함되어있는지 여부
cost = [1e13]*(V+1) # 각 정점에 연결되는 간선의 비용
def prim(v): # v: 시작 정점
cost[v] = 0 # 출발지는 0
# 모든 정점의 횟수만큼 탐색해야 함
for _ in range(V):
# 현재 정점에서 이동할 가장 최소 간선을 찾아야 함!
u, min_cost = -1, 1e13
for i in range(V+1):
# 아직 MST에 포함되어 있지 않은 최소 비용 간선 선택
if not MST[i] and cost[i] < min_cost:
min_cost = cost[i]
u = i
MST[u] = True
# 선택된 정점을 기준으로 모든 간선 비용 업데이트(cost)
for x, w in adjList[u]:
if not MST[x] and cost[x] > w:
cost[x] = w
return sum(cost[1:])
print(prim(1))# 우선순위 큐 사용
from heapq import heappop, heappush
V, E = map(int, input().split())
# 각 정점에 대한 정보는 인접리스트로 저장
adjList = [[] for _ in range(V+1)]
# 무방향 = 양방향이므로 양쪽 정점에 모두 저장
for _ in range(E):
a, b, c = map(int, input().split())
adjList[a].append((b, c))
adjList[b].append((a, c))
def prim(v):
MST = [False]*(V+1)
pq, cost = [], 0
# 간선에 대한 정보 저장 (비용, 도착 정점)
heappush(pq, (0, v))
while pq:
c, v = heappop(pq)
if MST[v]: # 이미 MST에 포함되어 있는 간선이면
continue
cost += c
MST[v] = True
for x, w in adjList[v]:
heappush(pq, (w, x))
return cost
print(prim(1))