[프로그래머스] Lv2. N-Queen

문제 링크

풀이

1️⃣ 내 풀이

chess : 각 행의 몇 번째 열에 체스가 놓여있는지 나타내는 1차원 배열
cols : 행에 상관없이 각 열에 체스가 놓여있는지를 나타내는 boolean 타입의 값을 갖는 1차원 배열

행이 1칸씩 증가하면서 체스를 놓게 된다. 이때 가능한 모든 열을 확인한다. 아직 사용되지 않은 열이 있다면 대각선으로 체스말이 놓여있는지를 확인한다. 현재 행에서부터 0행까지 반복문을 돌면서 갖고 있는 값이 현재 열에서 대각선으로 이동 가능한 값인지 확인한다.

def solution(n):
    answer = 0
    cols = [False]*n
    chess = [-1] * n

    def queen(row):
        nonlocal answer
        if row == n:
            answer += 1
            return 

        for c in range(n):
            if cols[c]:
                continue

            for r in range(row+1):
                if chess[row-r] in (c-r, c+r):
                    break
            else:            
                chess[row] = c
                cols[c] = True
                queen(row+1)
                cols[c] = False
                chess[row] = -1

    queen(0)
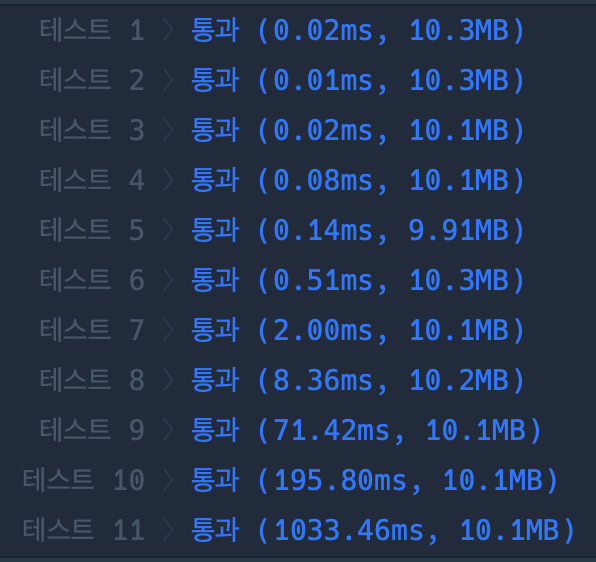
    return answer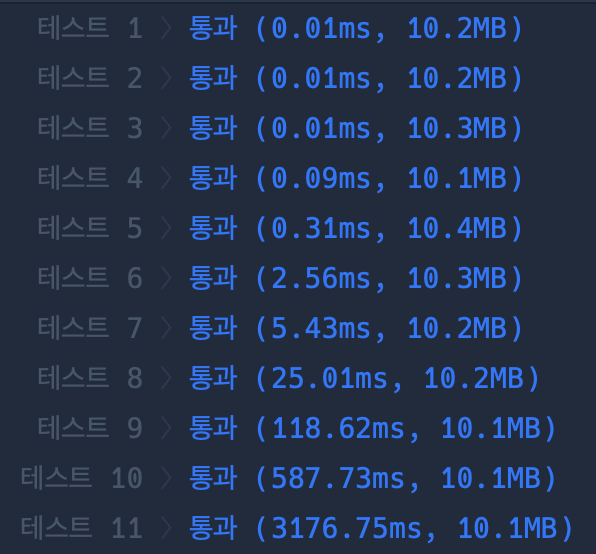

2️⃣ 다른 사람 풀이

diagonal1, diagonal2은 각 대각선에 체스말이 놓여있는가를 판단하는 1차원 배열이다. 대각선은 아래와 같다.

n=5라고 할 때

# 왼쪽 아래로 내려오는 대각선
  0 1 2 3
0 0 1 2 3
1 1 2 3 4
2 2 3 4 5
3 3 4 5 6

# 오른쪽 아래로 내려오는 대각선
  0 1 2 3
0 3 2 1 0
1 4 3 2 1
2 5 4 3 2
3 6 5 4 3

퀸은 대각선에 있는 말도 공격할 수 있으므로 같은 번호를 갖는 대각선에 이미 체스말이 놓여있다면 그 칸에는 체스말을 놓을 수 없다. 만일 오른쪽 아래로 내려오는 대각선에서 0행 2열에 체스말을 놓았다면 1번 칸에 체스말이 놓여있다. 같은 1의 값을 갖는 1행 3열에는 체스말을 놓을 수 없다.

이 방식은 매번 체스말을 놓을지 여부를 결정하려고 할 때마다 반복문을 돌려 각 행을 확인할 필요가 없으므로 시간복잡도가 훨씬 낮아진다.

def solution(n):
    answer = 0
    
    chess = [0]*n
    cols = [False]*n
    diagonal1, diagonal2 = [False]*(2*n), [False]*(2*n)
    print(diagonal1)
    def queen(row):
        nonlocal answer
        if row == n:
            answer += 1
            return 
        
        for col in range(n):
            if not cols[col] and not diagonal1[row+col] and not diagonal2[n-col+row]:
                cols[col] = True
                diagonal1[row+col] = True
                diagonal2[n-col+row] = True
                
                queen(row+1)
                cols[col] = False
                diagonal1[row+col] = False
                diagonal2[n-col+row] = False
                
    queen(0)
    return answer