[프로그래머스] Lv2. 당구 연습

문제

풀이

📐 대칭을 이용한 풀이

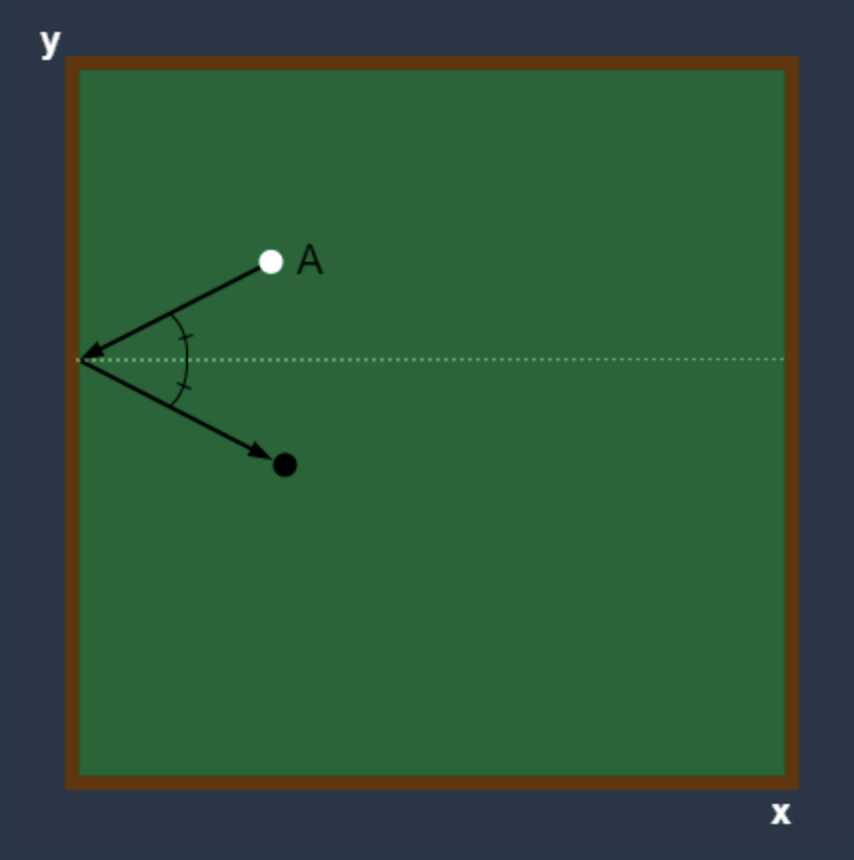
처음엔 닮음을 이용해 각각의 길이를 구해서 피타고리스 정리로 대각선 길이를 구하고 더하는 복잡한 식인줄 알았다. 그런데 입사각과 반사각이 같으니까 대칭으로 돌려서 하나의 큰 직각삼각형으로 만들고 그 대각선 길이를 구하는 문제였음

단, 이때 문제에 모서리에 대해서 언급이 되는데 모서리의 경우는 최소값이 나올 수가 없음

그림을 보면 공이 모서리와 아무리 가까워진다고 해도 모서리를 통해 대칭 시킬 경우 startX와 ballX의 값을 더한 값을 변수로 갖게 된다. 아래쪽을 통해 대칭 시켰을 때의 x 값은 startX-ballX 이므로

startX + ballX > startX - ballX

라서 항상 모서리에서 튕겨 나오는 값이 벽에 튕기는 값보다 클 수 밖에 없다.

그래서 모서리는 제외하고 4개 각각의 변에 대해서 불가능한 경우는 제외하고 가능한 경우만 dis 배열에 값을 담고 그 최소값만 추출

최종 코드

def solution(m, n, startX, startY, balls):
    answer = []
    
    for bx, by in balls:
        dis = [1e9] * 4
        
        if startX != bx or startY < by: # ↓
            dis[0] = (startY+by)**2 + (startX-bx)**2
        if startY != by or startX > bx: # →
            dis[1] = (m-startX+m-bx)**2 + (startY-by)**2
        if startX != bx or startY > by: # ↑
            dis[2] = (startX-bx)**2 + (n-startY+n-by)**2
        if startY != by or startX < bx: # ←
            dis[3] = (startX+bx)** 2 + (startY-by)**2
        
        print(dis)
        answer.append(min(dis))
    return answer