[프로그래머스] Lv2. 소수 찾기

🔍 문제

풀이

🥲 일반적인 소수 찾기(완전탐색)

현재 숫자 n의 루트 n까지의 숫자까지 일일이 나눠가면서 소수인지 아닌지를 판별한다. 하나라도 나눠 떨어지는 숫자라면 소수일 수 없다.

이 문제에서는 문제의 조건이 크지 않아서 가능했지만 아주 큰 숫자라면 시간초과가 발생할 가능성이 높음.

def prime_number(n):
    if n < 2:
        return 0
    
    if n in (2, 3, 5, 7):
        return 1
    
    for i in range(2, int(n**0.5)+1):
        if not n % i:
            return 0
    return 1
    

def solution(numbers):
    answer = 0
    perm = set()
    for r in range(1, len(numbers)+1):
        for num in permutations(numbers, r):
            num = int(''.join(num))
            perm.add(num)
    
    print(perm)
    for n in perm:
        answer += prime_number(n)
        
    return answer

from itertools import permutations

에라토스테네스의 체

def solution(nums):
    # nums에서 중복되지 않는 조합 구하기
    perm = set()
    for r in range(1, len(nums)+1):
        perm |= set(map(int, map("".join, permutations(list(nums), r))))
    
    # 0, 1은 제외
    perm -= set(range(0, 2))
    
    # 2, 3, 5, 7... 의 배수들 제외하기
    for i in range(2, int(max(perm)**0.5)+1):
        perm -= set(range(i * 2, max(perm)+1, i))
    
    return len(list(perm))
from itertools import permutations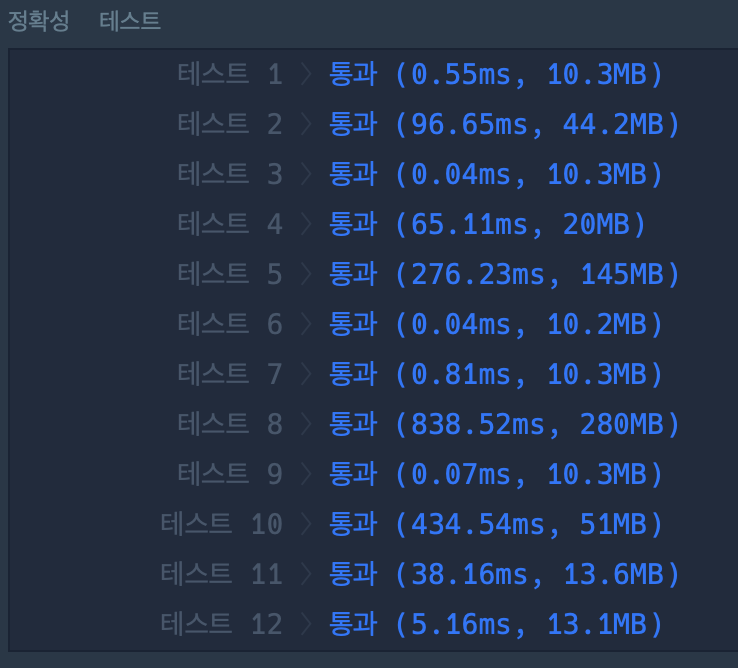

근데 이게 더 느린데