
🔗
💡 풀이 아이디어
(0, 0)에서 (N-1, N-1)까지 갈 수 있는 모든 경로 비용 중 최소 비용을 찾으라는 문제였다. 처음 보자마자 아무 생각 없이 그래프 탐색 문제라고 생각했고, 25x25=625니까 전부 탐색해도 무리없겠다 싶어서 완전 탐색을 돌렸다. 결론은 ❌
모든 경우를 탐색해서 찾는 건 시간초과가 났다. 그렇다면 매 순간 최선의 방식을 선택해서 탐색하는 방법 밖에 없었다. DP아니면 다익스트라를 사용할 수 있을 것 같았는데 모든 경로의 개수를 찾는 게 아니라 최소 비용만 찾으면 되기 때문에 DP는 아닌 것 같았다. 다익스트라를 사용해보기로 했다.
현재 위치에서 같은 방향으로 이동할 경우 100원, 방향이 변경되는 경우는 600원이 추가된다(경로 변경 + 직진). 이전 위치에서 현재 위치로 오기 위한 방향과 현재 위치에서 다음 위치로 가기 위한 방향이 같다면 100원이고, 그렇지 않다면 600원이 추가되는 셈이었다. 최소힙을 사용해서 구현했기 때문에 매번 가장 최소의 비용을 갖는 값들을 선택하면서 탐색해나가게 된다. 항상 최소 비용부터 탐색해나가기 때문에 더 큰 비용으로 같은 위치를 두 번 탐색할 수는 없다. 여기서도 그렇게 고려하고 구현했는데, 또 틀렸다.
중요한 건 방향
중요한 건 꺾이지 않는 마음이 아니라 방향이었다.
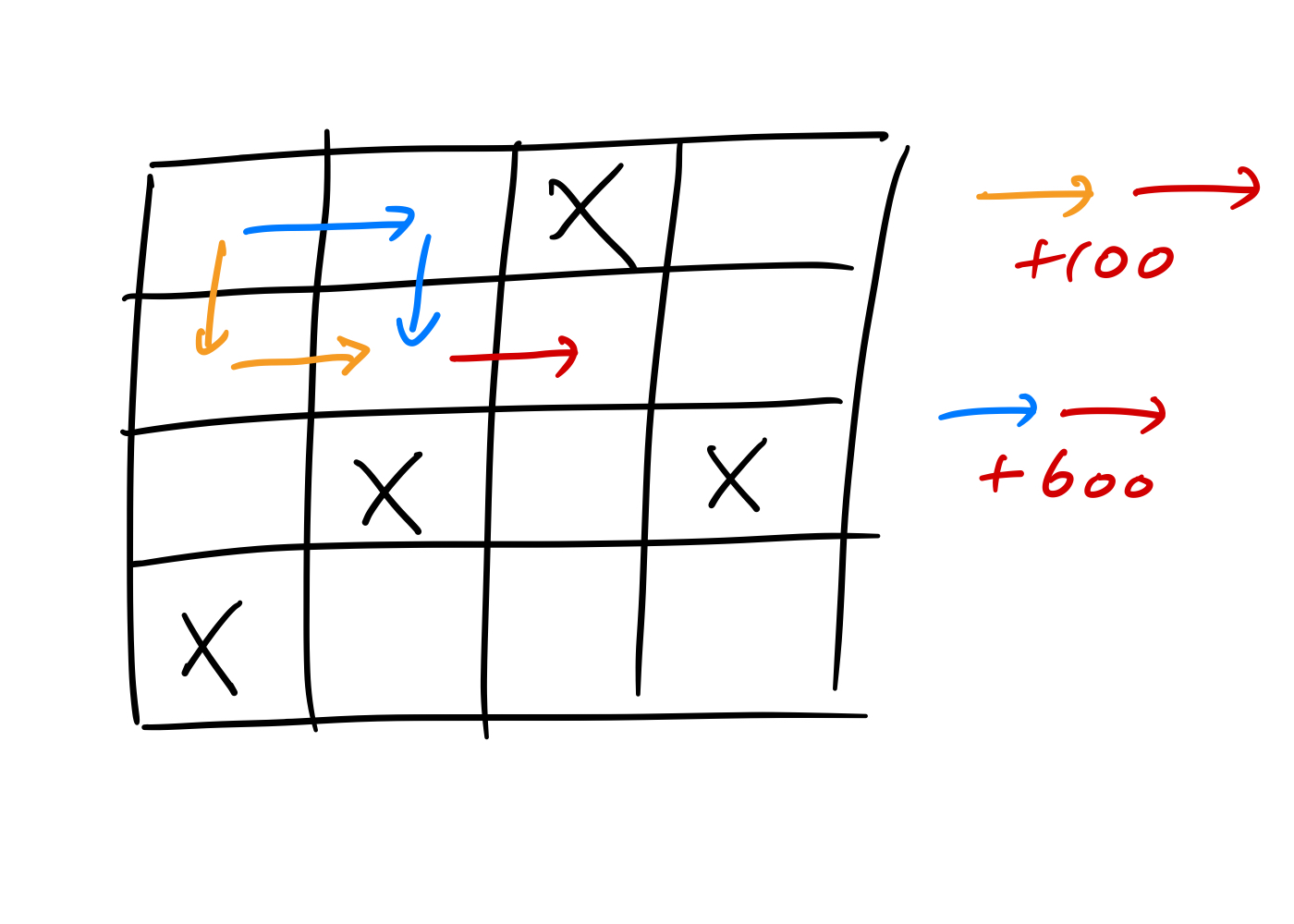
입출력 예제 3번을 보면 출발 위치에서 주황색과 파란색 두 가지 경로를 통해 (1, 1)에 도달할 수 있다. 둘 다 직선 도로와 코너가 각각 1번이기 때문에 (1, 1)에 도달할 수 있는 비용은 똑같다. 하지만 그 다음 경로인 빨간색으로 향할 때는 달라지게 된다.
주황색은 같은 방향으로 직진이기 때문에 100원만 추가되지만 파란색은 코너이기 때문에 600원이 추가된다. 즉, 특정 위치에 도달했을 때의 비용 뿐 아니라 어떤 방향을 갖고 도달하게 되었는지를 기록해야 하는 것이다. 현재 예제에서는 (1, 1)에 같은 비용으로 도달했기 때문에 단순히 비용이 같거나 클 때에는 도달할 수 있도록 수정하는 걸로 고칠 수 있지만, 실제 테케 중에는 주황색이 더 많은 비용으로 도달하고 파란색이 더 적은 비용으로 도달해서 아예 주황색이 (1, 1)에 도달할 수 없게 될 수도있다.
결국 왼쪽 방향으로 이동해서 도달했는지, 오른쪽 방향으로 이동해서 도달했는지 각각의 4개의 방향에 대해서 최소값을 다 따로 계산해야 한다. 방문처리 하는 visited 배열을 3차원으로 구현해서 4개의 방향에 대해 각각의 NxN배열을 따로 정의했다.
최종 코드
def solution(board):
N = len(board)
dirs = [(1, 0), (0, 1), (-1, 0), (0, -1)]
pq = [(-500, 0, 0, -1)]
visited = [[[1e9]*N for _ in range(N)] for _ in range(4)]
visited[0][0][0], visited[1][0][0], visited[2][0][0], visited[3][0][0] = 0, 0, 0, 0
while pq:
cost, x, y, d = heapq.heappop(pq)
if (x, y) == (N-1, N-1):
return cost
if visited[d][x][y] < cost:
continue
for i in range(4):
nx, ny = x+dirs[i][0], y+dirs[i][1]
if i == d:
next_cost = cost+100
else:
next_cost = cost+600
if -1<nx<N and -1<ny<N and board[nx][ny] != 1 and visited[d][nx][ny] >= next_cost:
visited[d][nx][ny] = next_cost
heapq.heappush(pq, (next_cost, nx, ny, i))
import heapq