
🔗
풀이
❌ 완전 탐색
가능한 경우의 수를 전부 다 구해서 사전순으로 정렬한 다음에 가장 앞의 값만 반환한다. 당연히 안 된다. 50x50이고 모든 칸에 다 방문할 수 있기 때문에 최대 2500개의 칸이 4방향의 값을 다 가질 수 있어 4^2500으로 시간 초과 발생
def solution(n, m, x, y, r, c, k):
x, y, r, c = map(lambda x: x-1, (x, y, r, c))
def dfs(x, y, route, depth):
nonlocal answer
if depth == k:
if (x, y) == (r, c):
answer.append(''.join(route))
return
if x<0 or y<0 or x>=n or y>=m:
return
depth += 1
dfs(x+1, y, route+['d'], depth)
dfs(x, y-1, route+['l'], depth)
dfs(x, y+1, route+['r'], depth)
dfs(x-1, y, route+['u'], depth)
answer = []
dfs(x, y, [], 0)
if answer:
answer.sort()
return answer[0]
return 'impossible'
import sys
sys.setrecursionlimit(5000)⭕️ DFS
일반적인 DFS... 최대 2500번까지 들어가기 때문에 파이썬의 재귀한도(999)를 늘려줘야 가능하다.
def solution(n, m, x, y, r, c, k):
distance = abs(r-x) + abs(c-y)
if distance > k or (k - distance)%2:
return 'impossible'
dxy = ((1, 0, 'd'), (0, -1, 'l'), (0, 1, 'r'), (-1, 0, 'u'))
def dfs(x, y, route, depth):
nonlocal answer
if k-depth < abs(r-x)+abs(c-y):
return
if (x, y, depth) == (r, c, k):
answer = route
return
for i in range(4):
nx = x+dxy[i][0]
ny = y+dxy[i][1]
nroute = route + dxy[i][2]
if 1<=nx<=n and 1<=ny<=m and nroute<answer:
dfs(nx, ny, nroute, depth+1)
answer = 'z'
dfs(x, y, '', 0)
return answer
import sys
sys.setrecursionlimit(5000)⭕️ 그리디
이 풀이를 그리디로 풀 수 있다는 힌트를 보고 시도했다.
이 문제에서 이동 경로는 크게 (1) 반드시 지나가야 하는 최단경로와 (2) 남는 잉여 거리동안 돌아다닐 경로가 존재한다.
✅ 반드시 지나가야 하는 최단경로
일반 그래프 탐색으로 푸는 방법도 있지만 이 문제에서는 그리디로 해결할 수 있다. 어차피 모든 칸이 방문가능하고, 사전 순서대로 방문하라고 했기 때문에 우리는 반드시 아래(d) → 왼쪽(l) → 오른쪽(r) → 위쪽(u) 순서대로 방문해야 한다. 때문에 가능한 이동 경로는 아래 8가지이다.
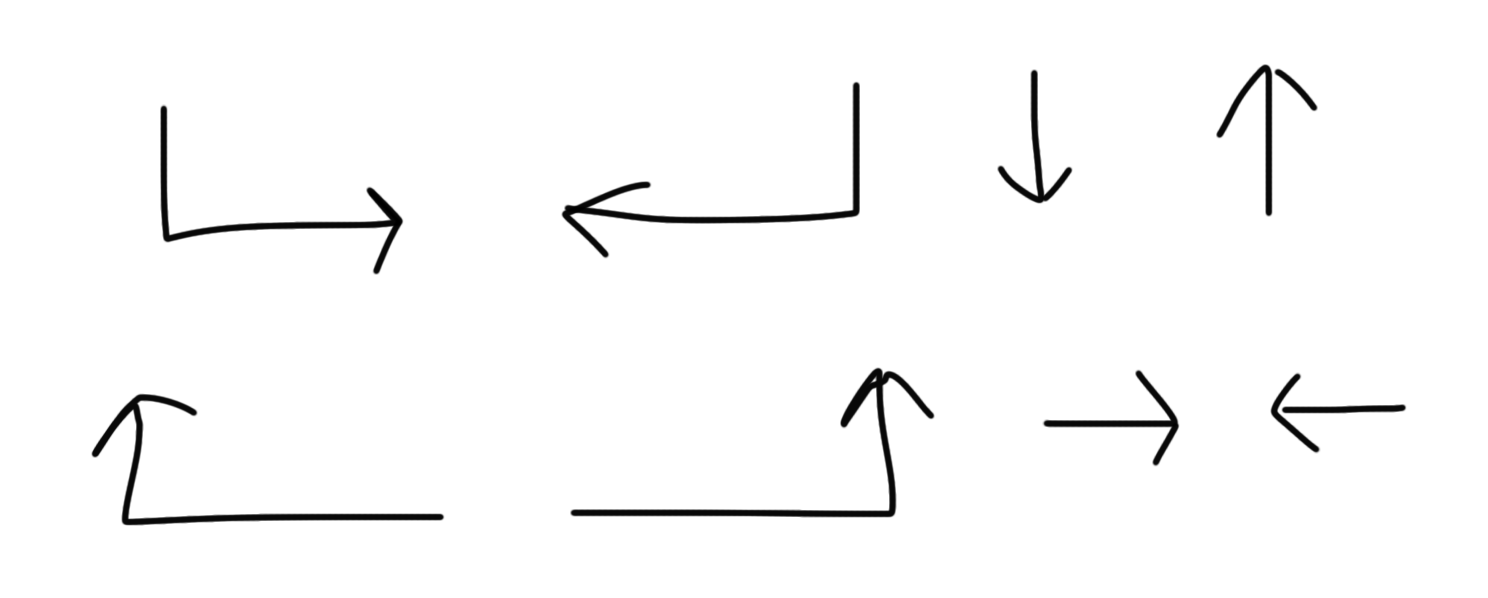
이 경로는 변경될 수 있는 경로가 아니라 반드시 이렇게 지나가야만 하는 경로이다. 언제 지나가게 될 지는 바뀔 수 있지만 어쨌든 도착지에 도착하기 위해서는 반드시 지나가야 한다. 이 경로는 출발 위치와 탈출 위치의 좌표값 계산을 통해 간단하게 구할 수 있다.
max를 통해 양수만 받아올 수 있도록 설정했다.
def find_short_distance(x, y, r, c):
down = max(r-x, 0)
left = max(y-c, 0)
right = max(c-y, 0)
up = max(x-r, 0)
return down, left, right, up🧐 남는 잉여 경로
문제에 주어진대로 사전순으로 가장 빠르면서 출발 → 탈출위치로 가는데는 영향을 주지 않는 경로여야 한다.
사전순 경로 :
d→l→r→u
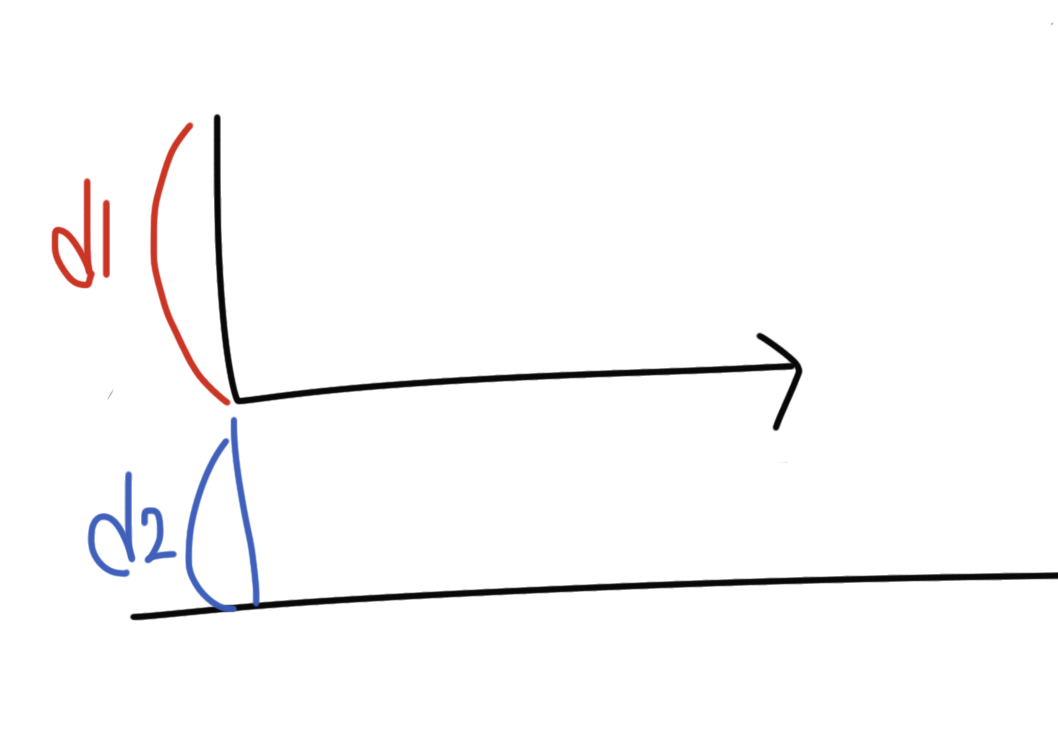
출발지에서 도착지에 가기 위한 최단경로에서 반드시 아래를 거쳐야 하는 경로는 d1 이다. 하지만 만약 탈출 위치에 도착하고도 여전히 10의 거리를 더 가야 한다면? 쉽게 생각하면 탈출 위치에 도착한 다음에 사전 순으로 빠른 방향인 아래로 내려가면 되지 않을까? 그런 다음 다시 위로 올라와서 제자리에 돌아온다면 10의 거리를 소모할 수 있을 것이다.
하지만 그렇게 되면 d → r(오른쪽) → 탈출 위치 → d → u가 된다. 이게 정말 사전순으로 빠른 방법일까?
생각해보면 굳이 탈출 위치에 먼저 도착한 다음에 잉여 거리를 가라는 말은 없었다. 그 말은 탈출 위치에 도착하기 전에 사전 순으로 빠른 방향들을 다 방문해도 된다는 말이다. 위 그림에서 보면 반드시 가야 하는 최단거리는 d1이라고 했고, 탈출 위치에 도착한 다음에 다시 아래로 더 내려갈 수 있는 거리는 d2이다. d1만큼 이동한 다음에 d2만큼 더 이동하는 게 사전순으로 가장 빠르다.
사전순으로 빠른 방향 순서대로 이동 가능할 때까지 이동할 것
아까 최단경로는 반드시 방문해야 하는 경로라고 했고, 잉여경로는 최단경로에 영향을 주지 않는 경로라고 했다. 이 말은 잉여 경로로 어떻게 이동하든 간에 다시 제자리로 돌아올 수 있도록 해야 한다는 것이다. 즉, 우리는 내려간 d2만큼 다시 올라와야 한다. 다만 여기서 문제는 올라오는 방향 u는 사전순에서 가장 느리다. 가장 나중에 나올 수록 좋은 단어라는 말은 가장 마지막에 이동하는 방향이 되어야 한다는 뜻이 된다.
그렇다면 여기서는 어디로 이동하는 게 좋을까? 만약 이동거리가 50정도 남았다고 하자. 현재 d1+d2만큼 이동한 위치에 있다고 가정할 때, 탈출 위치까지 오른쪽으로 대략 10을 이동해도 40 정도가 남고, d2만큼 위로 올라온다고 해도 어느 정도 남을 수 밖에 없다.
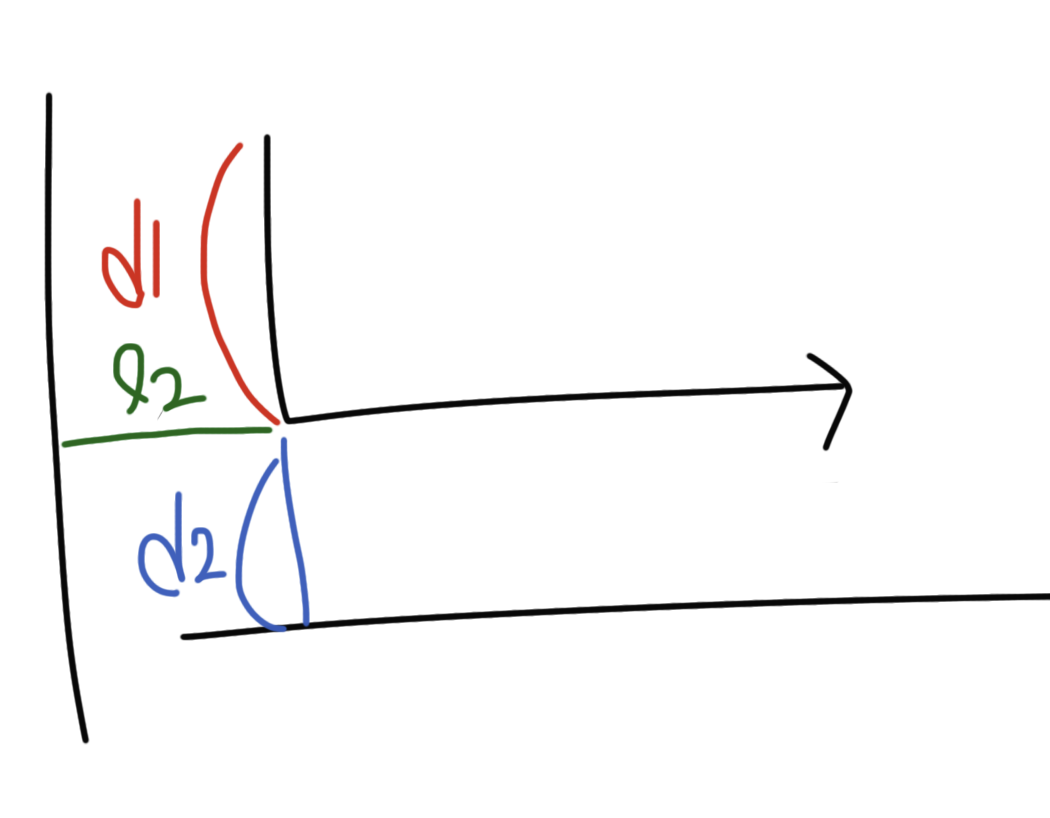
여기서 힌트는 또 사전순이 된다. 사실 여기서 더 내려갈 수 있는 곳은 없고, 올라오는 방향은 사전순으로 가장 느리니 피하는게 좋다. 오른쪽으로 계속 이동해서 탈출위치까지 가버리는 건 잉여 거리가 남으니 안된다. 하지만 위의 그림상으로 봤을 때 왼쪽으로 이동할 수 있는 거리가 남아있다. l은 두 번째 사전순이기 때문에 d가 등장할 만큼 등장한 다음에 등장한다면 사전순으로 빠르게 할 수 있는 최선의 선택이 될 수 있다. 그렇게해서 l2만큼 이동할 수 있게 된다.
그런데 이제 또 왼쪽으로 가기에는 또 길이 막혀있다. 그럼 오른쪽으로 갔다가 다시 왼쪽으로 이동하는 건? r → l이 되면 계속 양옆만 오고가면서 잉여거리를 소모할 수 있고, rrrr만으로 이동해버리는 것보단 rlrl이 사전순으로 좀 더 빠르다.
이제 잉여거리를 다 소모했다면 탈출 위치로 돌아가야 한다. l2만큼 왼쪽으로 이동한 잉여거리를 되돌리기 위해서는 l2만큼 오른쪽으로 이동해야 하고, d2만큼 이동한 잉여거리를 되돌리려면 d2만큼 위로 이동하면 된다.
현재까지의 이동순서를 나열하면 다음과 같다
d→l→rl→r→u
참고로 여기서 배열의 최소 크기는 2x2이기 때문에 왼쪽으로 갈 수 없으면 반드시 오른쪽으론 이동할 수 있고, 아래로 갈 수 없다면 반드시 위로는 갈 수 있다.
아래로 이동할 수 없다면 왼쪽으로, 왼쪽으로 더 이상 이동할 수 없다면 오른쪽 왼쪽을 번갈아가며 이동할 것. 잉여거리를 다 소모했다면 원상복귀하고 최단경로를 따라 탈출 위치로 가면 된다.
🫠 각 방향마다의 잉여거리 구하기
사실 잉여거리의 방향은 아래쪽과 왼쪽만 고려하면 된다. 아래로 내려간만큼 올라오면 되고, 왼쪽으로 간만큼 오른쪽으로 이동하면 되기 때문이다. 위로 올라가거나 오른쪽으로 가는 게 우선순위가 되면 사전순에서 뒤로 밀리기 때문에 애초에 고려하질 않는다.
생각해보면 잉여거리란 출발 위치에서 탈출 위치로 가는 길에 방문할 수 있는 방향에 있으면서 한 번에 이동이 가능해야 한다. 이미 사전순으로 우선순에 있는 순서대로 방문하고 있기 때문에 다시 뒤로 왔다가 가는 건 안 된다.
아래쪽을 예로 들었을 때, 만약 아래벽에 닿게 되면 아래로는 더 이상 이동할 수 없다. 위로 올라갔다가 아래로 내려가는 건 u이 나오면 사전순으로 뒤쳐지기 때문에 불가능하다. 반드시 왼쪽으로 이동해야 한다. 그런데 이때 왼쪽도 막혀있다면, 오른쪽으로 이동했다가 다시 왼쪽으로 오는 방향을 택해야 한다.
각 방향으로 잉여거리를 얼마나 이동할 수 있는가는 아래와 같이 구하게 된다. 왼쪽으로는 출발 위치와 탈출 위치 중 더 작은 열의 값을 갖는 값이 된다. 한번에 이동할 수 있는 최단거리 l1과 왼쪽벽에 닿기 직전까지 이동할 수 있는 거리(↔️, l2)가 되는 것이다.

아래는 좀 다르게 구하게 되는데, 행의 최대 길이(n)에서 각 위치 행을 뺀 값의 최소값을 구하면 된다.
d2, l2 = min(n-x, n-r), min(y-1, c-1)⭕️ 최종경로 O(1)에 구하기
아래로 이동하기
반드시 이동해야 하는 최단경로 d1과 잉여경로 d2가 있다. d1만큼은 반드시이동해야 하지만, d2는 잉여거리가 남아있을 때만 이동하게 된다. 여기서 잉여거리는 rem으로 표시된다. 그런데 아까 잉여경로는 최단경로에 영향을 주지않도록 다시 제자리로 돌아올 수 있게 하는 경로라고 했으므로 아래로 내려갔다면 나중에 다시 위로 올라오는 것까지 고려해야 한다. 아래로 내려가는 거리와 위로 올라오는 거리가 세트여야 하므로, 잉여거리가 6 정도 남았다면 아래로는 3만큼만 내려가야 다시 올라올 수 있는 거리 3이 남게 된다. 이 부분을 고려해서 잉여거리를 2로 나눈 값과 아래로 최대한 이동할 수 있는 잉여거리를 비교해 더 작은 값만큼 더해준다. 아래로 더 이상 내려갈 수 없는 경우와 잉여 거리가 남지 않은 경우를 고려해야 하기 때문이다.
'd'*(d1+min(rem//2, d2))왼쪽으로 이동하기
아래로 이동하는 것과 비슷하다. 다만, 아래로 이동한 잉여경로가 있다면 그만큼은 잉여거리에서 제외해야 한다. rem - d2*2는 아래로 이동할만큼 이동하고도 남은 잉여거리가. 아래로 내려갔다 올라오는것까지 고려해야 하므로 아래로 이동한 잉여거리값의 2배를 한 값을 전체 잉여거리에서 제외한다. 하지만 만약 잉여거리보다 아래로 이동할 수 있는 거리의 값이 더 클 수도 있으므로 이때 음수값이 나오지 않게 max(값, 0)으로 설정해 양수만 나올 수 있게 한다. 위에서와 마찬가지로 잉여거리와 이동가능한 왼쪽 잉여거리 중 더 짧은 쪽을 택할 수 있도록 한다.
'l'*(l1+min(max((rem-d2*2)//2, 0), l2))오른쪽 왼쪽 제자리 이동하기
아래와 왼쪽으로 이동한 잉여경로를 전체 이동거리에서 제외한 값만큼 이동하면 된다. 앞에서와 다르게 이 값은 rl로 애초에 쌍을 이루고 있기 때문에 2로 나눠줄 필요가 없다는 점을 고려한다.
'rl'*max((rem-d2*2-l2*2)//2, 0)오른쪽으로 이동하기
앞서 왼쪽으로 이동했던 만큼 이동하면 된다.
'r'*(r1+min(max((rem-d2*2)//2, 0), l2))위쪽으로 이동하기
앞서 아래로 이동했던 만큼 이동하면 된다.
'u'*(u1+min(rem//2, d2))전체 코드
def find_short_distance(x, y, r, c):
down = max(r-x, 0)
left = max(y-c, 0)
right = max(c-y, 0)
up = max(x-r, 0)
return down, left, right, up
def solution(n, m, x, y, r, c, k):
# 사전순 : d l r u
short = abs(x-r) + abs(y-c)
if short > k or (k-short)%2:
return "impossible"
rem = k-short
d1, l1, r1, u1 = find_short_distance(x, y, r, c)
d2, l2 = min(n-x, n-r), min(y-1, c-1)
answer = 'd'*(d1+min(rem//2, d2)) + 'l'*(l1+min(max((rem-d2*2)//2, 0), l2)) + 'rl'*max((rem-d2*2-l2*2)//2, 0) + 'r'*(r1+min(max((rem-d2*2)//2, 0), l2)) + 'u'*(u1+min(rem//2, d2))
return answer코드 수정
def solution(n, m, x, y, r, c, k):
# d l r u
dist = abs(r-x) + abs(c-y)
if dist>k or (k-dist)%2:
return 'impossible'
# 최단거리 : 탈출 위치와 현재 위치 사이의 거리... 가능한 방향...
d1 = max(r-x, 0)
l1 = max(y-c, 0)
r1 = max(c-y, 0)
u1 = max(x-r, 0)
# 잉여거리 : 출발이든 탈출이든 둘 중 어느 위치에서든간에 최단거리를 제외하고 갈 수 있는 남은 거리
# 아래와 왼만 고려
d2 = min(n-x, n-r)
l2 = min(y-1, c-1)
# 잉여경로
rem = k - dist
d_rem = min(rem//2, d2)
rem = max(rem-d2*2, 0)
l_rem = min(rem//2, l2)
rem = max(rem-l2*2, 0)
rl_rem = max(rem//2, 0)
# 경로구하기
route = 'd'*(d1+d_rem) + 'l'*(l1+l_rem) + 'rl'*rl_rem + 'r'*(r1+l_rem) + 'u'*(u1+d_rem)
return route