[프로그래머스] Lv3. 양과 늑대

🔗

풀이

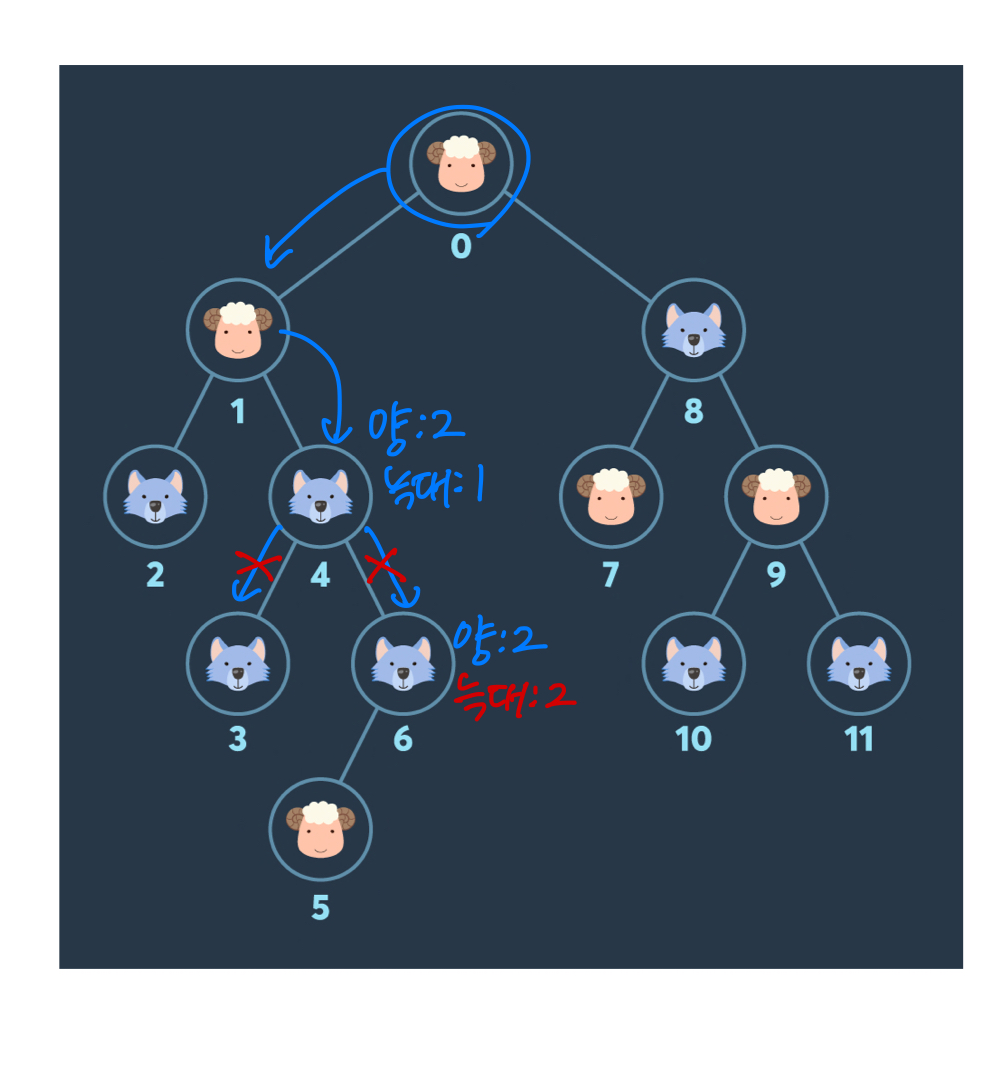
트리를 순회하면서 최대한 많은 양을 수집하는 게 문제의 목적이다. 단 순회 도중에 현재까지 모인 양의 개수가 늑대의 개수와 같아지면 늑대가 양을 모두 잡아먹게 되기 때문에 주의해야 한다. 늑대가 양을 모두 잡아먹게 되면 그 이후 노드로는 이동할 필요가 없다.

그림의 파란색 경로처럼 이동하면서 양과 늑대를 모을 수 있다. 늑대를 만나더라도 현재 가진 양의 개수가 늑대의 개수보다 많기만 하다면 지나칠 수 있다. 그러나 문제는 이렇게 위에서 아래로만 이동하지는 않는다.

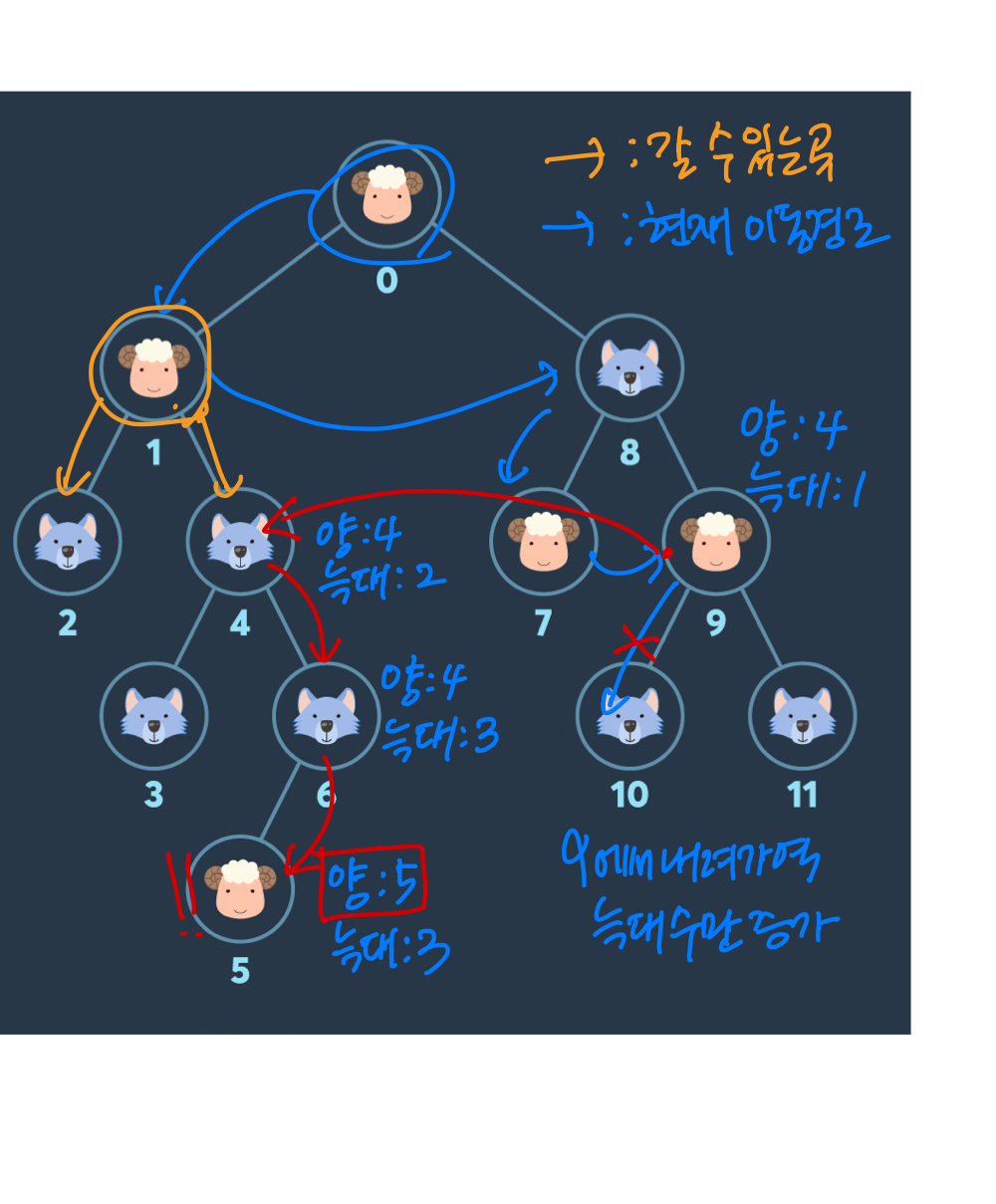
우선 부모 노드와 자식 노드의 형태로 구성된 트리 구조이기 때문에 부모 노드를 방문하면 그 이후에는 자식 노드를 방문 할 수 있다 하지만 꼭 방문 해야 하는 것은 아니다 특정 노드를 방문하고 나서 그 자식 노드들을 방문할 수 있는 노드들에 추가할 수는 있으나 바로 다음에 직접적으로 그 자식 노드들을 방문해야 하는 것은 아니라는 것이다.

첫 번째 그림에서 보면 부모 노드에서 자식 노드로만 이동하게 되면 도중에 양의 개수와 늑대의 개수가 같아지는 구간이 나타나서 최대한 모을 수 있는 양의 개수는 2개 밖에 안 된다.

하지만 두 번째 그림의 파란색 경로를 보면 0 -> 1 -> 8 -> 7 -> 9 와 같이 이동하고 있다. 이는 부모-자식 노드로 경로가 제한된 것이 아니라, 특정 노드를 방문한 후 그 자식 노드들을 방문할 수 있는 노드에 추가하고 방문할 수 있는 노드들 중 하나의 노드를 골라서 방문하는 식으로 경로를 이동하고 있기 때문이다. 즉 0번 노드를 방문하 1번과 8번 노드를 방문할 수 있다. 1번을 방문하면 2, 4번을, 8번을 방문하면 7, 9번을 방문할 수 있다. 이런식으로 방문할 수 있는 노드들에 가능한 노드를 모두 추가하고 최대한의 양의 개수를 모을 수 있는 경로들을 찾으면 된다. 이때 깊이 우선 탐색을 사용하게 된다.

그림을 보면 9번 노드 이후에 아래로 내려가게 되면 늑대만 1마리 추가되고, 그 아래에는 더 이상 양이 없다. 그러므로 굳이 늑대의 개수를 늘리면서 10번이나 11번을 갈 필요가 없다. 대신 1번 노드를 방문하면서 방문 가능한 노드에 추가됐었던 4번 노드를 방문한다. 늑대의 개수가 1 증가하지만 양의 개수가 4이기 때문에 잡아먹히지 않는다. 그대로 6번 노드를 방문하면 이제 양이 있는 5번 노드를 방문할 수 있게 되고, 양의 개수 5, 늑대의 개수 3으로 최대 양의 개수 5를 얻을 수 있게 된다.

1. 특정 노드를 방문하면 그 노드의 자식 노드들을 방문 가능한 노드에 추가
2. 특정 노드에서 방문 가능한 노드들 가운데 하나를 골라서 이동
3. 양의 개수 = 늑대의 개수가 되는 노드를 만나면 return 한다. 여기서는 더 이상 이동해도 양의 개수가 늘어날 수 없다.

import java.util.*;

public class Solution {

    List<List<Integer>> grassLand = new ArrayList<>();
    int maxSheep;
    int[] _info;

    public int solution(int[] info, int[][] edges) {
        _info = info;
        for (int i = 0; i < info.length; i++) {
            grassLand.add(new ArrayList<>());
        }

        for (int[] edge : edges) {
            grassLand.get(edge[0])
                     .add(edge[1]);
        }

        dfs(0, new int[]{0, 0}, new ArrayList<>());
        return maxSheep;
    }

    public void dfs(int now, int[] state, List<Integer> queue) {
        state[_info[now]] += 1;
        maxSheep = Math.max(maxSheep, state[0]);
        if (state[0] <= state[1]) return;

        queue.addAll(grassLand.get(now));
        for (int i = 0; i < queue.size(); i++) {
            int next = queue.get(i);
            queue.remove(i);
            dfs(next, Arrays.copyOf(state, 2), queue);
            queue.add(i, next);
        }
        queue.removeAll(grassLand.get(now));
    }
}