[프로그래머스] Lv3. 여행경로

🔗

풀이

이런 경우를 생각해야 한다.

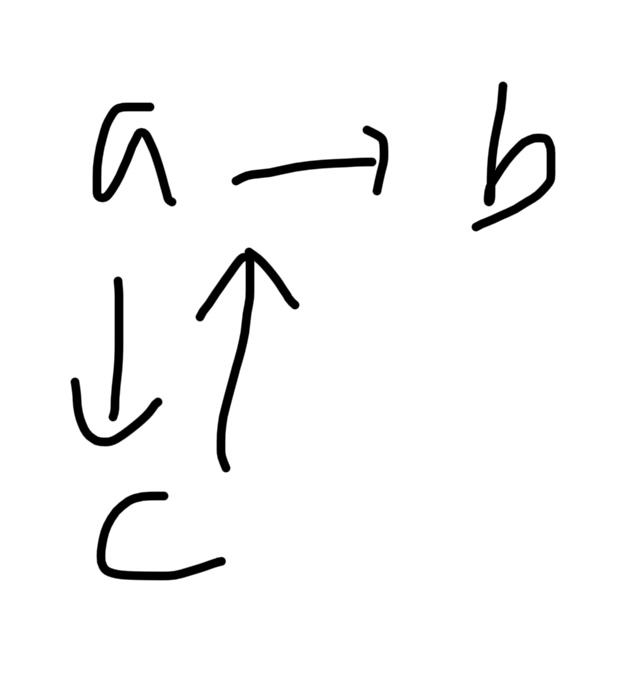
알파벳 순서라서 a에서 b로 먼저 가야하지만 b에서는 더 이상 갈 수 있는 곳이 없어서 다시 a로 되돌아와야 한다. 현재 출발지에서 방문할 수 있는 목적지를 스택에 추가한다. 그런 다음 스택의 가장 끝에 있는값(스택은 LIFO)를 출발지로 설정한다. a에서 b로 출발지가 변경되는데, b는 더 이상 갈 수 있는 목적지가 없으므로 다시 a로 되돌아올 수 있어야 한다. b는 스택에서 제거하고 최종적으로 구하려는 route에 추가한다.

a로 되돌아오면 b는 이미 방문했으므로 c를 방문한다. c에서는 a로 다시 되돌아올 수 있는 경로가 존재하므로 a -> c -> a가 된다. 이번에 다시 되돌아온 a에는 더 이상 방문할 수 있는 목적지가 없으므로 스택에서 꺼내 route에 추가해야 한다.

아래는 스택에 쌓이는 출발지들과 경로의 형태이다

stack, route

[a] []
[a, b] []
[a], [b]
[a, c] [b]
[a, c, a] [b]
[a, c] [b, a]
[a], [b, a, c]
[], [b, a, c, a]

최종 경로는 route를 역으로 반환하면 된다. a → c → a → b이다.

def solution(tickets):
    graph = defaultdict(list)
    for a, b in sorted(tickets, reverse=True):
        graph[a].append(b)
    
    route, stack = [], ['ICN']
    while stack:
        
        while graph[stack[-1]]:
            stack.append(graph[stack[-1]].pop())
        route.append(stack.pop())
    
    return route[::-1]

from collections import defaultdict

유사한 문제

리트코드의 332. Reconstruct Itinerary도 같은 코드로 풀린다