[프로그래머스] Lv3. 합승 택시 요금 (2021 카카오 공채)

🔗

풀이

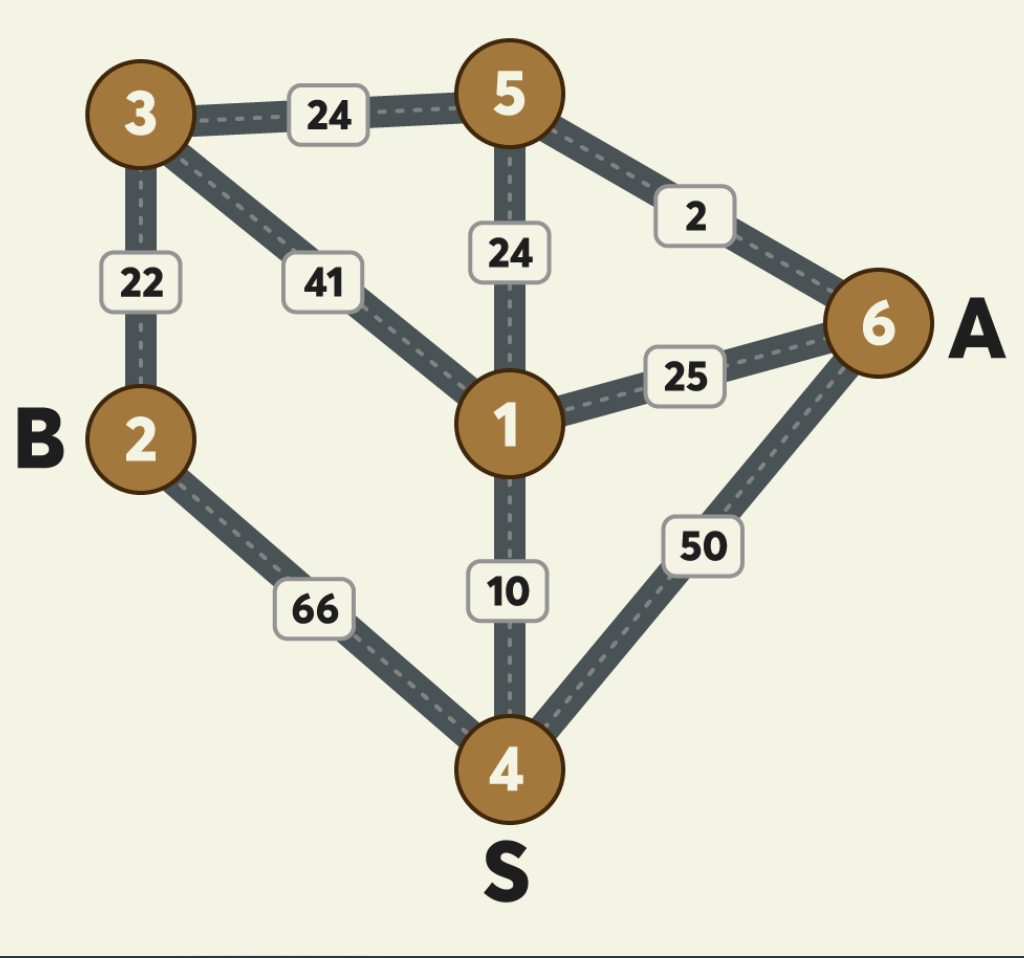
정점 s에서 출발하여 a, b로 갈 수 있는 최소 비용을 찾아야 한다. 처음 출발점부터 각각의 방향을 향해 갈 수도 있지만 그렇지 않은 경우도 존재할 수 있다. 그럴 경우 겹치는 경로는 같이 택시를 탄다고한다. 같은 경로를 지나가게 될 경우 돈은 한 번만 낸다는 것이다. 그럼 만약 정점 x까지 택시를 탄다고 치면 s-x로 가는 경로 + x에서 a로 가는 경로 + x에서 b로 가는 경로가 최소 비용이 되지 않을까?

s~x로 가는 경로 + x~a로 가는 경로 + x~b로 가는 경로

플로이드 워셜 알고리즘을 사용해서 모든 정점에서 다른 모든 정점으로 가는 최소비용을 구해도 되지만 여기서는 그냥 다익스트라를 사용했다. 우선 출발 정점에서 각 정점까지의 최소비용을 구한 후 모든 정점을 돌면서 다익스트라를 통해 다른 모든 정점까지의 최소비용의 값을 갖는 배열을 반환, 거기서 최소 비용을 구해 더하는 방식으로 구했다.

def dijkstra(graph, s, n):
    cost = [1e9]*(n+1)
    cost[s], queue = 0, [(0, s)]
    while queue:
        c, now = heapq.heappop(queue)
        
        if cost[now] != c:
            continue
            
        for _next, cc in graph[now]:
            if cost[_next] > c + cc:
                cost[_next] = c + cc
                heapq.heappush(queue, (c + cc, _next))
                
    return cost
    
def solution(n, s, a, b, fares):
    graph = defaultdict(list)
    for c, d, f in fares:
        graph[c].append((d, f))
        graph[d].append((c, f))
    
    cost, ans = dijkstra(graph, s, n), 1e9
    for i in range(1, n+1):
        cost_i = dijkstra(graph, i, n)
        ans = min(ans, cost[i] + cost_i[a] + cost_i[b])
        
    return ans
    
from collections import defaultdict
import heapq