Segment tree 구현

0. Segment Tree

Segment Tree는 Node에 해당하는 Segment의 연산 결과를 저장하는 자료 구조이다.

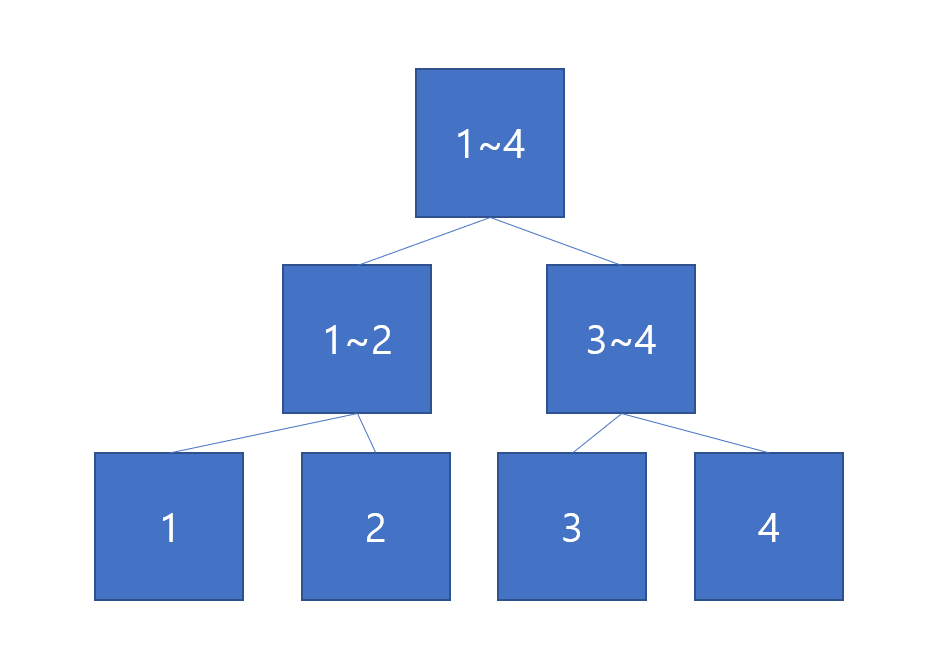
• 위의 그림과 같이 루트 노드에는 index(1~4)의 연산 결과를 저장하고, 자식 노드는(1~2), (3~4)의 연산 결과를 갖고 있는 Tree이다.
• tree의 index를 1부터 시작할 때 left child의 index는 parent의 idx *2 이고, right child의 index는 parent의 idx*2+1 이 된다.
• 1~3은 해당 연산이 합일 때를 기준으로 작성했다.

1. init

init(node, start, end) 함수는 tree[node]를 결정 하는 함수이다. tree[node]는 자식 노드들의 합이고 이를 재귀적으로 구현이 가능하다. 모든 Node에 대해 연산을 수행해야 하므로 O(nlogn)의 시간 복잡도를 가진다.

def init(node, start, end):
	# start == end 일 때 더이상 쪼개질 수 없어 자식 Node 이다.
    if start == end:
        tree[node] = arr[start]
        return tree[node]
    tree[node] = init(node * 2, start, (start + end) // 2) + init(node * 2 + 1, (start + end) // 2 + 1, end)
    return tree[node]

2. update

update(node, start, end, idx, diff) arr의 idx번 값을 diff 만큼 변경 시키는 연산을 의미한다. 이는 트리의 depth만큼 시간복잡도를 가지므로 O(log n)의 시간 복잡도를 가진다.

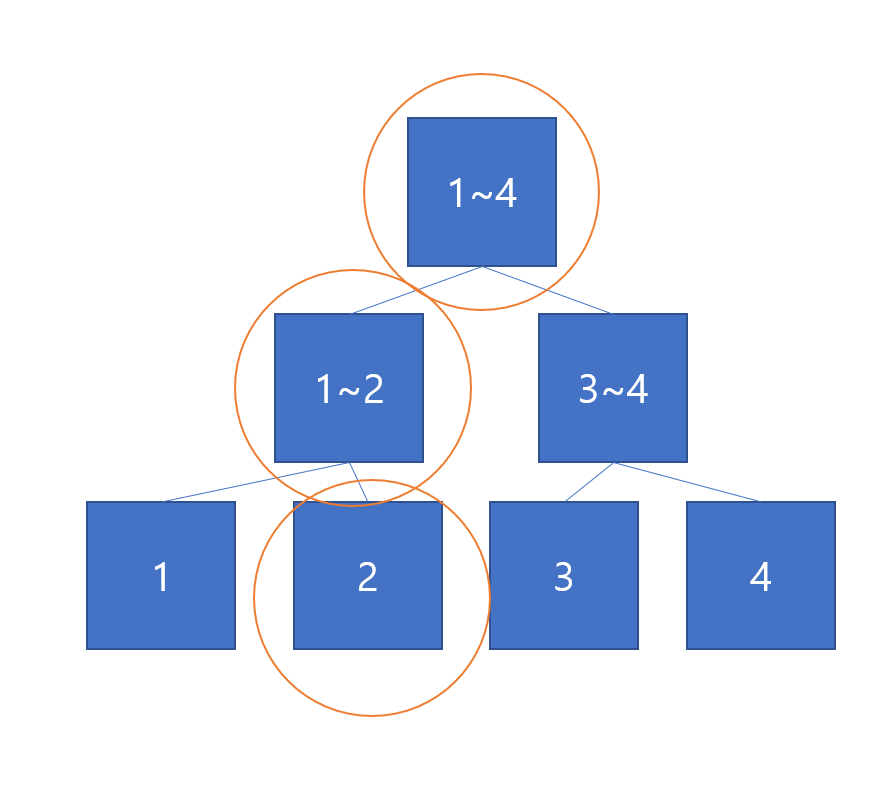
2번 인덱스를 업데이트 하려면 2번 index에 해당하는 값을 업데이트 하기위해선 주황색 원안의 Node의 값을 변경해야 한다.

def update(node, start, end, idx, diff):
    # idx 를 포함하지 않으면
    if start > idx or idx > end:
        return
    # 포함하는 경우 이므로 update
    tree[node] += diff
    # leaf가 아니면 자식 update
    if start != end:
        update(node * 2, start, (start + end) // 2, idx, diff)
        update(node * 2 + 1, (start + end) // 2 + 1, end, idx, diff)

3. query

query(node, start, end, left, right) arr의 left ~ right의 합에 해당하는 값을 리턴한다.

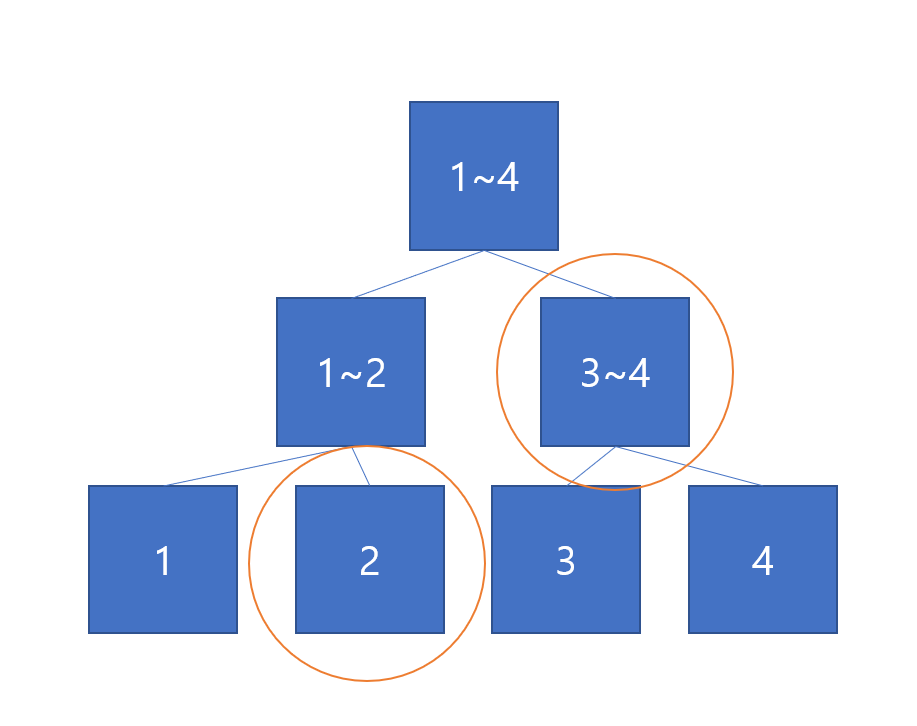
2~4번 합을 구하기 위해서는 주황색 원안의 Node의 합을 구하면 된다.

def query(node, start, end, left, right):
    # 범위 밖이면 return 0
    if start > right or left > end:
        return 0
    # start ~ end의 값이 left ~ right안에 속하면 해당 Node는 포함된다.
    if left <= start and end <= right:
        return tree[node]
    # left, right 내에 완전히 속하지 않고 intersection이 있으면 자식 노드에 대해 연산을 수행한다.
    return query(node * 2, start, (start + end) // 2, left, right) + query(node * 2 + 1, (start + end) // 2 + 1, end,
                                                                           left, right)

관련 문제
https://www.acmicpc.net/problem/2042 (boj 구간 합 구하기)

import sys

MX = 1010101
tree = [0 for _ in range(MX * 4)]
arr = [0 for _ in range(MX)]


def init(node, start, end):
    if start == end:
        tree[node] = arr[start]
        return tree[node]
    tree[node] = init(node * 2, start, (start + end) // 2) + init(node * 2 + 1, (start + end) // 2 + 1, end)
    return tree[node]


def update(node, start, end, idx, diff):
    if start > idx or idx > end:
        return
    tree[node] += diff
    if start != end:
        update(node * 2, start, (start + end) // 2, idx, diff)
        update(node * 2 + 1, (start + end) // 2 + 1, end, idx, diff)


def query(node, start, end, left, right):
    if start > right or left > end:
        return 0
    if left <= start and end <= right:
        return tree[node]
    return query(node * 2, start, (start + end) // 2, left, right) + query(node * 2 + 1, (start + end) // 2 + 1, end,
                                                                           left, right)


n, m, k = map(int, sys.stdin.readline().split())
for i in range(1, n + 1):
    arr[i] = int(sys.stdin.readline())
init(1,1,n)
for i in range(m + k):
    kind, x, y = map(int, sys.stdin.readline().split())
    if kind == 1:
        diff = y - arr[x]
        update(1, 1, n, x, diff)
        arr[x] = y
    if kind == 2:
        sys.stdout.write(str(query(1, 1, n, x, y)) + '\n')