
레드블랙 트리의 동작
레드블랙 트리가 자가 균형 이진 탐색 트리인만큼, Insert나 Delete된 노드가 있을 때 그 속성이 깨지면 다시 복구시켜주는 동작이 필요하다. 그것을 Insert-Fixup(T, z)과 Delete-Fixup(T, x)이란 함수들로 복구시켜준다.
cf.
Insert-Fixup(T, z)와 Delete-Fixup(T, x)의 z, x는 각각 의미하는 노드가 다르다. Insert-Fixup에서 z는 새로 들어온 노드를 의미하고 Delete-Fixup에서x는 삭제된 z를 대체하는 값을 가리키는 노드를 의미한다. 즉 이중흑색노드를 의미한다.
새로운 노드가 삽입 or 삭제되었을 경우 4, 5번 조건을 유지하기 위해 색 변환을 하고 회전을 진행해주면서 복구를 시켜준다.
색변환
-
상향 색 변환 (Color Promotion)
부모 노드의 두 자식 노드가 모두 붉은 노드이면 부모 노드를 붉은 노드로 바꾸고 자식 노드는 검은 노드로 바꿀 수 있다. -
하향 색 변환 (Color Demotion)
자식 노드가 붉은 노드이면 부모 노드를 검은 노드로 바꾸고 자식 노드를 붉은 노드로 바꿀 수 있다.
회전
-
우회전 (Right Rotation)
-
좌회전 (Left Rotation)
회전의 목적은 RBT의 속성 4번을 복구시켜주기 위함이다. 즉, 레드 노드가 자식노드로 검정색 노드를 가져야 한다는 속성을 말한다. (다른 식으로 설명하면 레드 노드가 연속적으로 존재할 수 없다는 뜻)
레드 노드는 연속되어 있으면 안되므로 몰려 있는 레드를 해결해주기 위해 색깔을 바꿔주고 회전을 시켜준다. (회전을 하고 색깔을 바꿔줘도 무방!)

무엇을 기준으로 회전할 지가 매우 중요하다.
기준이 된다고 하는 것은 회전 후에 해당 노드가 루트 노드가 되는 것을 의미한다.
그림의 경우, Right-Rotate(T, P), Left-Rotate(T, Q) 인데 이때 Right-Rotate(T, P)를 할 경우 P가 루트노드가 되고 P의 오른쪽 자식이었던 B가 Q의 왼쪽 자식이 된다. 한편, Left-Rotate(T, Q)를 할 경우 Q가 루트노드가 되고 Q의 왼쪽 자식이었던 B가 P의 오른쪽 자식이 된다.
정리

초록색 케이스는 몰려있는 레드를 색변환과 회전을 통해 해결해주려고 하는 것이다.
먼저, 몰려 있는 레드인 10, 20을 떨어뜨려 놓기 위해 20의 레드 하나를 위로 넘기려고 하는데, Red Black 트리의 특성을 유지하면서 넘기려면 회전을 사용해야 한다.
이때 회전한 이후에도 레드블랙트리의 속성인 루트노드의 색깔은 검정색이어야 한다를 만족하려면 20의 색깔과 50의 색깔을 바꿔줘서 회전 후 20이 루트가 되었을 때에도 검정색이 되게 해야 한다.
따라서 먼저 20과 50의 색깔을 바꿔주고, 20을 기준으로 회전해서 rbtree의 속성을 복구시켜줄 수 있다.
파란색 케이스는 그냥 색변환만 해서 해결해주는 경우이다. 10과 20이 레드로 몰려있었는데 이것을 해소하기 위해 20과 50의 색깔을 바꿔주면 된다.
Left-Rotation(T,z) 수도코드

수도코드를 어떻게 봐야 하는지 순서가 헷갈린다면, 예시로 위의 코드에서 두 번째 라인인 x.right = y.left를 보자. 한 마디로, y의 left에 있는 자식노드를 x의 right가 가리키는 곳에 대입해준다고 생각하면 된다.
여기서, left와 right 필드는 모두 포인터 변수이므로 구체적인 노드의 값이 아니라 가리키는 곳이라고 생각해주면 된다.
삽입 (Insert)

Rbtree도 이진 검색 트리의 일종인만큼, 삽입하는 노드의 값과 루트 노드의 값을 비교해서 가장 밑의 리프 노드로 삽입해주는 방식이다. (동일) 그러나 마지막 14 ~ 17라인이 이진 검색 트리의 삽입과 다른데, 14~15 라인은 Rbtree의 구조를 유지하기 위해 z 자식 노드를 T->nil로 설정해주고, 삽입되는 노드의 색깔은 Red로 하여 Black Height를 유지시켜준다. 그리고 마지막으로, 특성 중 위반되는 게 있는지 없는지 확인하여 특성을 복구시켜주는 함수인 Insert-Fixup(T, z)를 호출한다.
cf. 부모노드가 빨강색이었을 경우 레드 노드가 연속되면 안되기 때문에 재조정이 필요하다.
삽입 (Insert-Fixup)
삽입의 Fixup은 z 노드라는 새로운 노드가 들어왔을 때 아래 세 가지 케이스만 이해하면 된다.
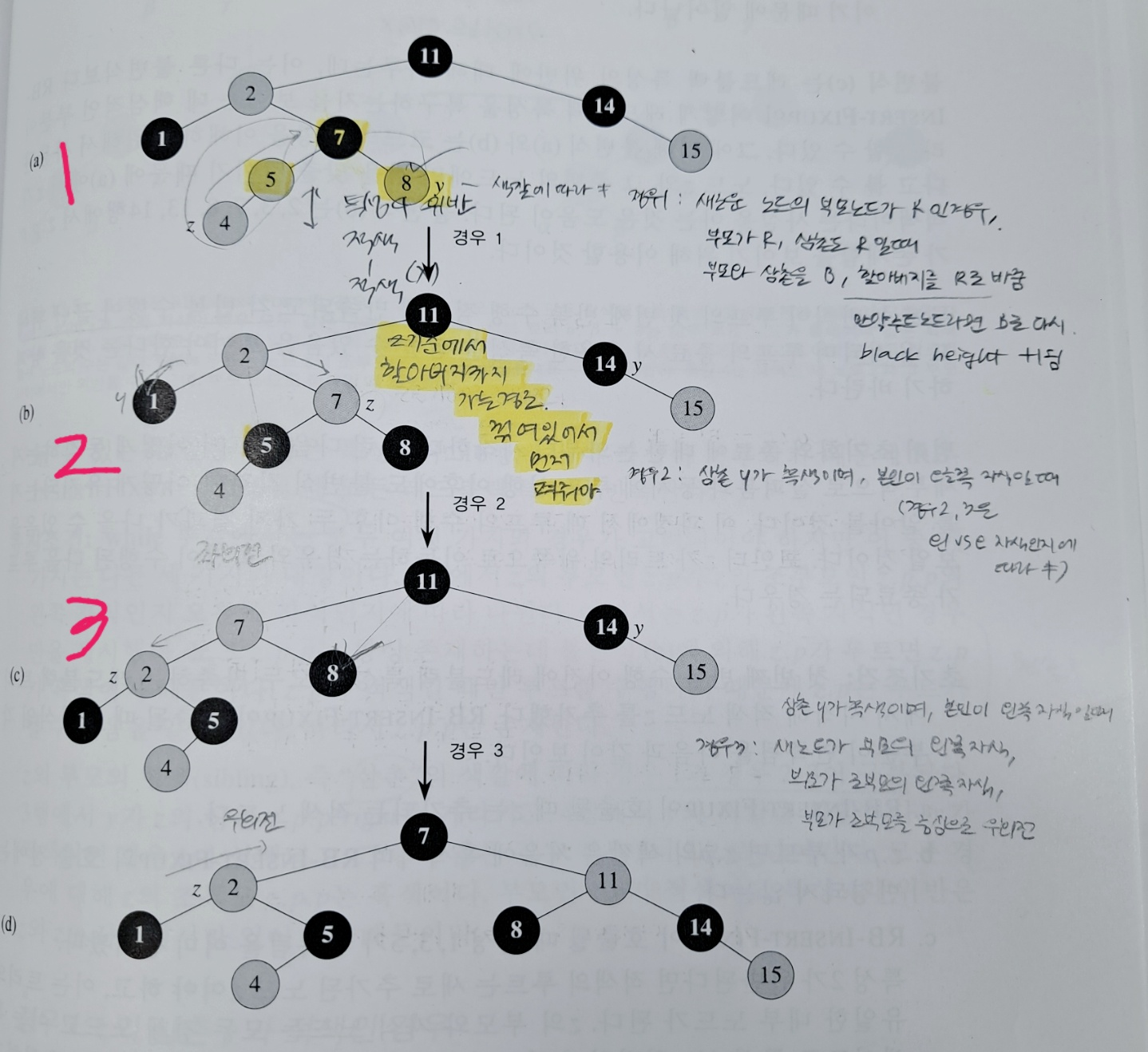
Insert-Fixup(T, z) 수도코드

