📖실수 표현 방식
실수(real number)는 양 또는 음의 값을 갖는 모든 정수, 0, 유리수, 무리수를 통틀어 일컫는 말이다. 컴퓨터에서는 숫자를 2진수로 저장하므로 실수 또한 우리가 익숙한 10진수가 아닌 2진수로 나타낼 수 있어야 한다.
📁실수를 2진수로 변환하기
실수를 정수부와 소수부로 나눈다고 했을 때, 먼저 정수부를 2진수로 변환하는 과정은 다음과 같다.
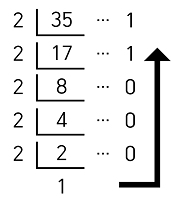
10진수를 나머지가 1이 될 때까지 2로 나눠 나머지를 구하고, 구한 나머지들을 밑에서부터 읽는다. 예를 들어, 35를 2진수로 나타내면 100011이고, 100011을 다시 10진수로 나타내면 2^5 + 2^1 + 2^0 = 35이다.
소수부는 정수부와 반대로 2를 계속 곱하는 방식으로 2진수로 변환된다. 소수부가 모두 정수가 될 때까지 2를 곱하고, 2를 곱해 만들어진 정수를 2진수로 변환하여 소수점 아래에 적는다.
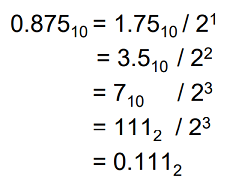
예를 들어, 0.875에 2를 곱하면 1.75, 1.75에 2를 곱하면 3.5, 3.5에 2를 곱하면 7이 된다. 이때, 7을 2진수로 나타내면 111이므로 0.875를 2진수로 표현하면 0.111이다. 0.111을 다시 10진수로 나타내면 2^(-1) + 2^(-2) + 2^(-3) = 0.5 + 0.25 + 0.125 = 0.875이다.
이렇게 2진수로 변환한 실수를 컴퓨터에서 표현하는 방식에는 고정 소수점과 부동 소수점이 있다.
📁고정 소수점
고정 소수점(fixed point)는 실수에서 소수부의 자릿수를 미리 정해 고정된 자릿수만큼의 소수를 표현하는 방식이다. 32bit 고정 소수점 방식은 다음과 같이 비트를 나눈다.
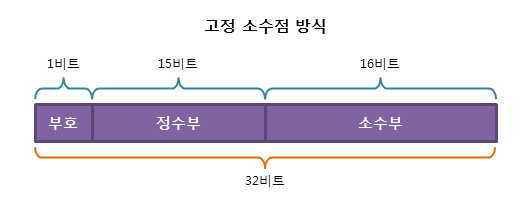
맨 앞 1비트는 부호를 나타내는 sign bit로, 0은 양수, 1은 음수를 나타낸다. 예를 들어, 10진수 -10.875를 고정 소수점 방식으로 표현하면 1 000 000 000 001 010 111 000 000 000 000 0이다.
📁부동 소수점
부동 소수점(floating point)는 실수를 정수부와 소수부로 나누는 것이 아니라, 가수부와 지수부로 나누어 표현하는 방식이다. 현재 사용되고 있는 부동 소수점 방식은 대부분 IEEE 754 표준을 따르고 있다.
32비트의 float형 실수를 IEEE 부동 소수점 방식으로 표현하면 다음과 같다.
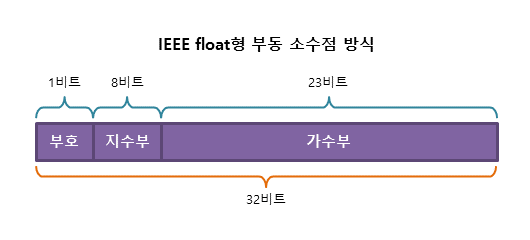
(-1)^(부호) x (1.가수부) x 2^(지수부 - 127)을 계산하면 10진수로 변환할 수 있다.
실수에서 가수부와 지수부를 구하기 위해서는 정규화를 해야한다. 2진수에서의 정규화는 정수부에 1만 존재하도록 실수를 표현하는 것이다. 예를 들어, 0.0101 = 1.01 x 2^(-2), 11.011 = 1.1011 x 2로 표현한다. 이때, 소수점 아래 부분을 가수부라고 한다. 지수부는 2의 지수에 bias라는 정해진 값을 더해 구하는데, IEEE float형 부동 소수점 방식에서 bias는 127이다. 지수부를 항상 양수로 나타내기 위해 bias를 127로 정해 더하는 것이다.
예를 들어, 10진수 0.875를 2진수로 변환하면 0.111이다. 0.111을 정규화하면 1.11 x 2^(-1)이므로 가수부는 110 00000 00000 00000 00000이고, 지수부는 -1 + 127 = 01111110이다.
64비트의 double형 실수를 IEEE 부동 소수점 방식으로 표현하면 다음과 같다.
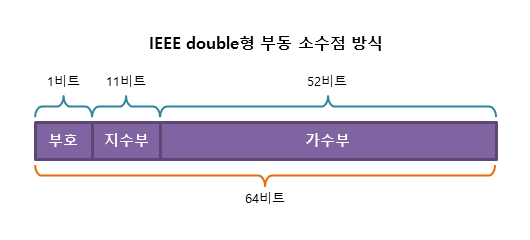
이 경우, bias는 1023이다.