📖패리티 비트
패리티 비트(parity bit)는 정보의 전달 과정에서 오류가 생겼는지를 검사하기 위해 추가되는 비트로, 1 bit의 오류를 찾아낼 수 있다.
패리티 비트를 포함한 데이터에서 1의 개수가 짝수인지 홀수인지에 따라 짝수 패리티, 홀수 패리티라고 한다.
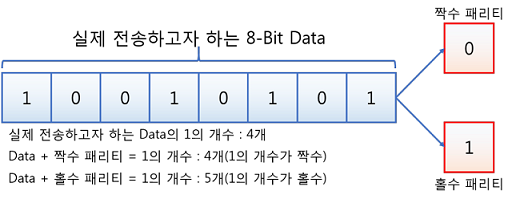
위와 같은 8 bit 데이터를 전송할 때 맨 끝에 패리티 비트를 추가하여 전송한다고 하면, 짝수 패리티의 경우 100101010, 홀수 패리티의 경우 100101011이 된다.
이렇게 패리티 비트를 정하여 데이터를 보내면, 데이터를 받는 쪽에서는 수신된 데이터의 전체 비트를 계산하여 패리티 비트를 다시 계산하는 것으로 데이터에 오류가 발생했는지를 확인할 수 있다.
그러나, 패리티 비트로는 오류가 발생했다는 사실만 확인할 수 있을 뿐, 어느 비트에서 오류가 발생했는지 알 수 없기 때문에 알맞은 데이터로 수정할 수는 없다. 데이터 재전송을 요청해야 한다. 또한, 하나가 아닌 2개의 비트에서 오류가 발생하면 오류 발생을 검출해내지 못한다.
📖해밍 코드
해밍 코드(hamming code)는 데이터 전송 시 1 bit의 에러를 정정할 수 있는 오류정정부호(ECC - Error Correction Code)의 일종이다.
패리티 비트를 데이터의 비트 수에 따라 필요한만큼 사용하여 데이터에 추가하고, 패리티 비트를 조합하여 에러 검출 및 교정을 수행한다. 데이터의 비트 수에 따라 필요한 패리티 비트의 개수는 다음과 같다.
2^p >= d + p + 1 (p : 패리티 비트 수, d : 데이터 비트 수)
예를 들어, 4 bit 데이터를 전송하기 위해서는 패리티 비트가 적어도 3개 필요하므로 해밍 코드는 7 bit가 된다.
해밍 코드에서 패리티 비트는 2의 거듭제곱에 해당하는 순서에 삽입된다. 즉, 비트 1, 비트 2, 비트 4, 비트 8, ...의 위치에 패리티 비트를 삽입한다.
❓해밍 코드 예제
4 bit 데이터 1011에 대해 짝수 패리티로 해밍 코드를 생성하는 과정은 다음과 같다.
4 bit 데이터를 전송하기 위해서는 패리티 비트가 적어도 3개 필요하므로 해밍 코드는 총 7 bit가 되고, 패리티 비트는 비트 1, 비트 2, 비트 4의 위치에 삽입된다.
| 비트 위치 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 패리티 1 | 패리티 2 | 데이터 1 | 패리티 3 | 데이터 2 | 데이터 3 | 데이터 4 |
각각의 패리티 비트의 값을 생성하고, 그 패리티 비트가 오류를 검출할 비트 그룹은 다음과 같다.
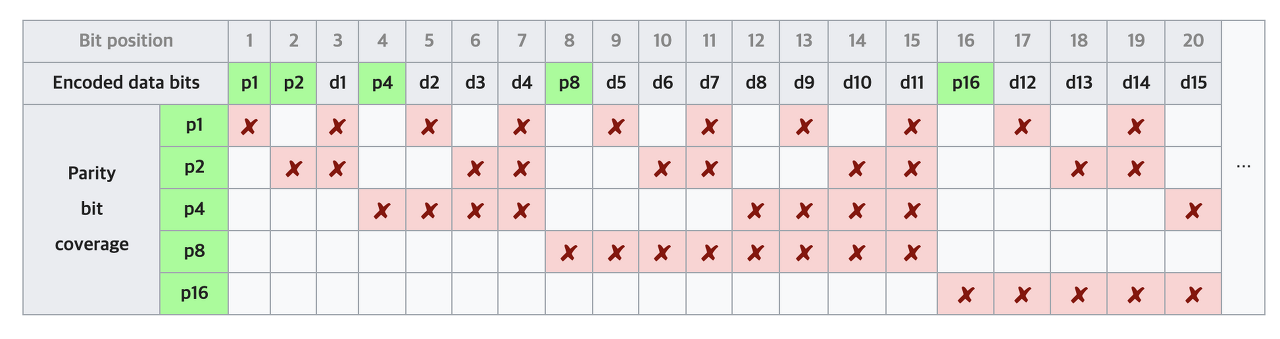
첫번째 패리티 비트는 데이터 비트 1, 2, 4에 의해, 해밍 코드로 보면 비트 3, 5, 7에 의해 값이 생성되고, 오류를 검출함을 알 수 있다. 각각의 패리티 비트가 해밍 코드의 어떤 비트 그룹을 담당하는지는 다음과 같이 계산할 수 있다.

짝수 패리티를 사용하므로 해밍 코드의 비트 3, 5, 7의 값이 각각 1, 0, 1일 때, 첫번째 패리티 코드의 값은 0이다. 같은 방식으로 패리티 비트 2의 값은 1, 패리티 비트 3의 값은 0이다. 따라서 해밍 코드는 0110011이다.
| 비트 위치 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| (패리티 1) | (패리티 2) | (데이터 1) | (패리티 3) | (데이터 2) | (데이터 3) | (데이터 4) |
이때, 전송한 데이터에서 비트 5(데이터 비트 2)가 0이 아닌 1로 잘못 전송되었다고 하면 오류 검출 과정은 다음과 같다.
p1 :1,3,5,7에서 1의 개수가 홀수이므로 오류 발생, p = 1
p2 :2,3,6,7에서 1의 개수가 짝수이므로 오류 발생하지 않음, p = 0
p3 :4,5,6,7에서 1의 개수가 홀수이므로 오류 발생, p = 1
오류가 발생한 경우, p값을 모아 몇번째 비트에서 오류가 발생했는지 알 수 있다. 이 경우, 101이므로 해밍 코드의 5번째 비트에서 오류가 발생했고, 비트의 값을 0으로 고치면 알맞은 데이터를 얻을 수 있다.