파이썬 알고리즘 인터뷰 14장_트리 개요

2023.11.26.일요일 대전 알고리즘 스터디 1장_트리 발표를 준비하면서 정리한 자료.

트리란?

• 트리는 계층형 트리 구조를 시뮬레이션 하는 추상 자료형(ADT)으로, 루트 값과 부모-자식 관계의 서브트리로 구성되며, 서로 연결된 노드의 집합이다
  1. 시뮬레이션 = 데이터 구조가 실제 나무와 같은 계층적 구조를 컴퓨터에서 모방하고 있다는 뜻
  2. 추상 자료형(ADT Abstract Data Type) '데이터의 타입과 그 데이터에 수행할 수 있는 연산들에 대해 정의하지만, 실제 내부의 구현은 숨기는 것을 의미합니다.
  • 트리 ADT는 일반적으로 다음과 같은 연산들을 정의할 수 있습니다:
    1. 삽입(Insertion): 새로운 노드를 트리에 추가하는 연산입니다. 이 연산은 트리의 규칙을 유지하면서 적절한 위치에 노드를 추가해야 합니다.
    2. 검색(Search): 주어진 값을 가진 노드를 찾는 연산입니다. 이는 트리를 순회하면서 값을 비교하여 원하는 노드를 찾습니다.
    3. 삭제(Deletion): 특정 노드를 트리에서 제거하는 연산입니다. 자식 노드가 있는 경우, 삭제 과정에서 트리의 구조를 재조정해야 할 수도 있습니다.
    4. 순회(Traversal): 트리의 모든 노드를 시스템적으로 방문하는 연산으로, 이는 전위(pre-order), 중위(in-order), 후위(post-order), 레벨 순서(level-order) 등 여러 방식으로 수행될 수 있습니다.
    5. 최소값/최대값 찾기: 트리 내에서 가장 작은 값 혹은 가장 큰 값을 가진 노드를 찾는 연산입니다.
    6. 노드 개수 계산: 트리에 있는 총 노드의 수를 계산하는 연산입니다.

트리 특징

1. 루트 값: 트리 구조에서 가장 상위에 위치하는 노드를 '루트(root)' 노드라고 합니다. 이 노드는 부모가 없는 유일한 노드입니다.
2. 부모-자식 관계의 서브 트리로 구성:
   • 각 노드는 하나의 부모 노드를 가지고 있을 수 있으며, 0개 이상의 자식 노드를 가질 수 있습니다. 이런 관계를 가진 노드들이 모여 '서브트리(subtree)'를 형성합니다. 즉, 한 노드 아래에 더 많은 노드들이 연결되어 있는 구조를 말합니다.
3. 서로 연결된 노드의 집합:
   • 트리는 서로 '연결'된 여러 노드들로 이루어져 있습니다. 노드란 트리의 기본 단위로, 데이터를 담고 있는 컨테이너와 다른 노드로의 링크(즉, 포인터)를 가지고 있습니다.
   • 이러한 노드들이 모여 전체적인 트리 구조를 만듭니다. 각 노드는 자신의 부모 노드와 자식 노드들과 '연결'되어 있으며, 이를 통해 트리 구조를 형성합니다.

트리 명칭

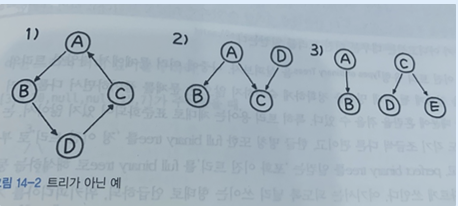
그래프 vs 트리

return if(순환 구조) ?  graph :  tree

트리

• 무조건 단방향(순환구조X)
• 하나의 부모
• 하나의 루트

그래프

• 단방향 or 양방향
• 부모 무조건 하나는 아님
• 루트 없음
  

트리 계의 두 형님(트리에서 자주 쓰이는 자료구조)

이진 트리

1. 이진 트리 : 모든 노드의 자식(degree)가 2개 이하인 트리
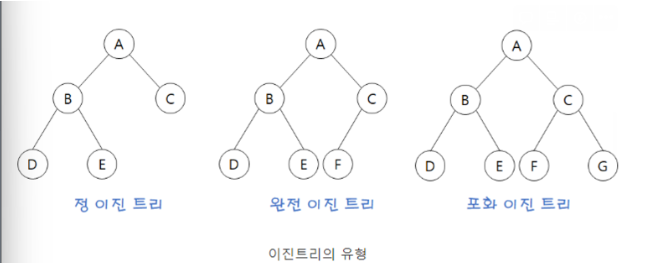
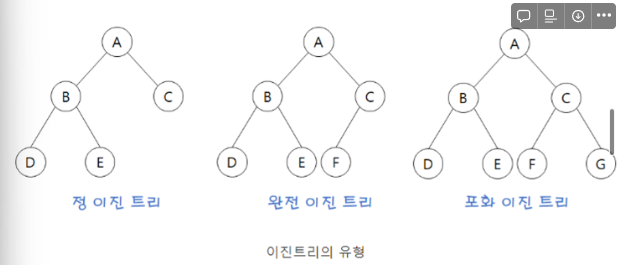
   1. (마지막 레벨) 자식 노드가 0개 혹은 2개 ⇒ full binary , 정 이진 트리
   2. (마지막 레벨을 제외) 꽉 차있다 ⇒ complete binary, 완전 이진트리
   3. (마지막 레벨을 제외) 모든 자식 노드가 2개이고 모든 리프가 같은 레벨이다 ⇒ perfect binary포화 이진
   

이진 탐색 트리 (그리고 최소 높이 트리)

• 이진 탐색 트리 (BST):
  - 이진 탐색 트리는 각 노드가 최대 두 개의 자식을 가지는 트리
  - 어떤 노드의 왼쪽 서브트리에 있는 모든 값은 그 노드의 값보다 작고, 오른쪽 서브트리에 있는 모든 값은 그 노드의 값보다 큽니다.
  - BST에서 최소 높이를 유지하는 것은 중요한데, 이는 탐색, 삽입, 삭제 작업의 효율성을 보장합니다. 최소 높이가 아닌 BST는 성능 저하의 원인이 될 수 있습니다.
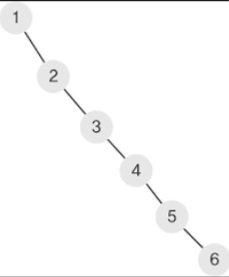
  - BST가 최소 높이를 유지하지 못하고, 완전히 불균형한 상태일 때, 즉 트리가 사실상 선형 구조(Linked List와 유사)로 퇴화되었을 때 최악의 경우가 발생합니다.
  - 불균형상태 탐색 O(n)
  - 균형상태 ⇒ log2n
  - 100개 카드 에서 A♠ 찾기 7번에 가능
  - 불균형 상태 예)
  
• 자가 균형 이진 탐색 트리
  - BST에서 삽입, 삭제 시 높이를 최소 높이를 유지하는 트리