시간복잡도

시간복잡도란 주어진 문제를 해결하기 위한 연산 횟수를 말합니다.

시간 복잡도 정의하기

실제 시간복잡도를 정의하는 3가지 유형은 다음과 같습니다.

• 빅-오메가: 최선일 때(best case)의 연산 횟수를 나타낸 표기법
• 빅-세타: 보통일 때(average case)의 연산 횟수를 나타낸 표기법
• 빅-오: 최악일 때(worst case)의 연산 횟수를 나타낸 표기법

예시

다음은 1~100사이의 무작윗값을 찾아 출력하는 코드입니다.

빅-오메가 표기법의 시간복잡도는 1번
빅-세타 표기법의 시간 복잡도는 N/2 번
빅-오 표기법의 시간 복잡도는 N번입니다.

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

int main() {
	int findNumber;
    srand(time(NULL));
    findNumber = rand() %100;
    
    for(int i = 0;  i< 100; i++){
    	if(i == findNumber){
        	cout << i;
            break;
        }
    }
}

코딩 테스트에서는 어떤 시간 복잡도 유형을 사용해야 할까?

코딩 테스트에서는 빅-오(O(n)) 을 기준으로 수행 시간을 계산하는 것이 좋습니다.
그 이유는 실제 테스트에서는 1개의 테스트 케이스로 합격, 불합격을 결정하지 않습니다. 다양한 테스트 케이스를 통과해야만 합격으로 판단하므로 시간 복잡도를 판단할 때는 최악일 때 (worst case) 를 염두에 둬야 합니다.

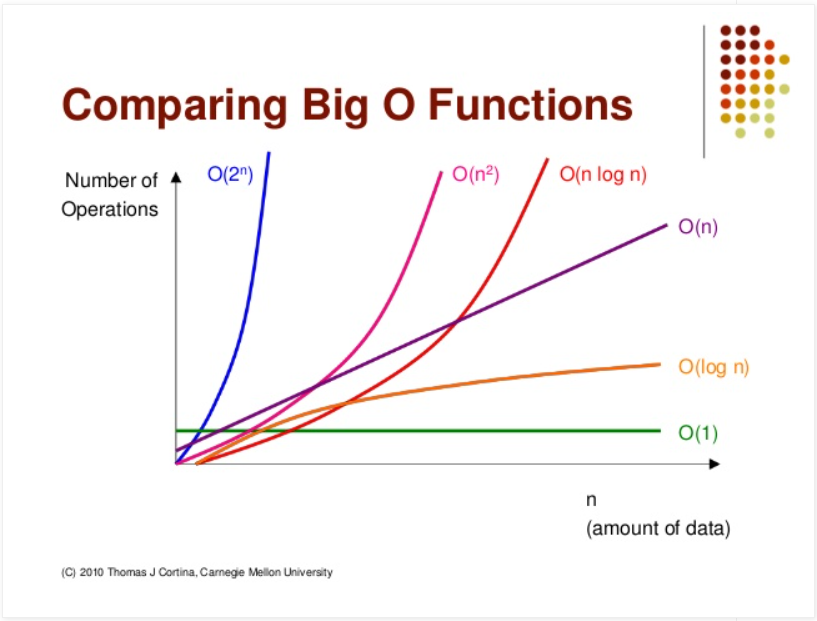
사진 출처: http://devwebcl.blogspot.com/2016/12/big-o-comparison.html

시간 복잡도 활용하기

알고리즘 선택의 기준으로 사용하기

https://www.acmicpc.net/problem/2750

문제
N개의 수가 주어졌을 때, 이를 오름차순으로 정렬하는 프로그램을 작성하시오.

입력
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.

출력
첫째 줄부터 N개의 줄에 오름차순으로 정렬한 결과를 한 줄에 하나씩 출력한다.

예제 입력

5
5
2
3
4
1

예제 출력

1
2
3
4
5

본 문제의 시간 제한이 2초이므로 이 조건을 만족하려면 2억 번 이하의 연산 횟수로 문제를 해결해야 합니다, 따라서 문제에서 주어진 시간 제한과 데이터 크기를 바탕으로 어떤 정렬 알고리즘을 사용해야 할 것인지를 판단할 수 있습니다.

💡연산 횟수는 1초에 1억번 연산하는 것을 기준으로 생각합니다.
💡시간 복잡도는 항상 최악일 때, 즉 데이터의 크기가 가장 클 때를 기준으로 합니다.

연산 횟수 계산 방법

• 연산 횟수 = 알고리즘 시간 복잡도 n값에 데이터의 최대 크기를 대입하여 도출

알고리즘 적합성 평가

• 버블 정렬 = (1,000,000)^2 = 1,000,000,000,000 > 200,000,000 -> 부적합 알고리즘

• 병합 정렬 = 1,000,000log2 (1000,000) = 약 20,000,000 < 200,000,000 -> 적합 알고리즘

문제에 주어진 시간제한이 2초이므로 연산 횟수 2억 번안에 원하는 답을 구해야합니다. 버블 정렬은 약 1조의 연산횟수 필요하므로 이 문제에 적합한 알고리즘은 아니라고 판단됩니다. 병합 정렬은 약 2000만 번읜 연산 횟수로 답을 구할 수 있으므로 문제에 적합한 알고리즘이라고 판단할 수 있습니다.

이와 같이 시간 복잡도를 분석으로 문제에서 사용할 수 있는 알고리즘을 선택할 수 있고, 이 범위를 바탕으로 문제의 실마리를 찾을 수 있습니다. 즉, 데이터의 크기 (N) 을 단서로 사용해야하는 알고리즘을 추측해 볼 수 있습니다.

시간 복잡도를 바탕으로 코드 로직 개선하기

시간 복잡도는 작성한 코드의 비효율적인 로직을 개선하는 바탕으로 사용할 수 있습니다. 이 부분을 활용하려면 시간 복잡도를 도출할 수 있어야 하빈다. 시간 복잡도를 도출하려면 다음 2가지 기준을 고려해야 합니다.

시간 복잡도 도출 기준

① 상수는 시간 복잡도 계산에서 제외한다.
② 가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다.

코드를 예로 들어 설명하겠습니다.

예제 1: 연산횟수 = N

int main() {
	int N = 1000;
    int cnt = 1;
    for (int i = 0; i < N; i++ ) {
    	cout << "연산 횟수: " << cnt++ << "\n";
        }
}

예제 2: 연산 횟수 = 3N
int main() {
	int N = 1000;
    int cnt = 1;
    for (int i =0; i< N; i++){
    	cout<< "연산 횟수: " << cnt++ << "\n";
        }
     for (int i =0; i< N; i++){
    	cout<< "연산 횟수: " << cnt++ << "\n";
        }
      for (int i =0; i< N; i++){
    	cout<< "연산 횟수: " << cnt++ << "\n";
        }

두 예제 코드의 연산 횟수는 3배 차이가 나지만 코딩 테스트에서는 일반적으로 상수를 무시하므로 두 코드 모두 시간 복잡도는 O(n) 으로 모두 같습니다.

다음 예제코드를 확인해보겠습니다.

int main() {
	int N = 1000;
    int cnt = 1;
    
    for( int i = 0; i < N; i++) {
    	for(int j =0; j < N; j+=) {
        	cout << "연산 횟수: " << cnt++ << "\n";
        }
        }
}

시간 복잡도는 가장 많이 중첩된 반복문을 기준으로 도출하므로 이 코드에서 이중 for 문이 전체 코드의 시간 복잡도의 기준이 됩니다. 만약 일반 for 문이 10개 더 있다 하더라도 도출 기준에 따라 시간 복잡도의 변화없이 N^2 으로 유지 됩니다.

이와 같이 자신이 작성한 코드의 시간 복잡도를 도출할 수 있다면 실제 코딩 테스트에서 시간 초과가 발생했을 때 이 원리를 바탕으로 문제가 되는 코드 부분을 도출할 수 있고, 이 부분을 연산에 더욱 효율적인 구조로 수정하는 작업으로 문제를 해결할 수 있습니다.

본 포스팅은 <Do It: 알고리즘 코딩 테스트 (C++)> 편의 내용을 보고 정리한 글입니다.