내리막 길 (백준, Java)

https://www.acmicpc.net/problem/1520

틀린 아이디어

모든 경우의 수를 구하는 것이 목표이기 때문에 BFS / DFS 방식을 사용해서 풀 수 있을 것 같았다. BFS는 최단거리를 구하는데 최적화 되어 있고, DFS는 경우의 수를 구하는데 최적화 되어 있으므로 DFS를 사용했으나, 시간초과가 발생했다.

public static void dfs(int[][] map, int nowY, int nowX, int[][] visited){
		// 도착하면 백
		if(nowY == map.length-1 && nowX == map[0].length-1){
			count++;
			return;
		}
		for(int i=0;i<4;i++){
			int newY = nowY + y[i];
			int newX = nowX + x[i];
			if(0 <= newY && newY < map.length
			&& 0 <= newX && newX < map[0].length
			&& visited[newY][newX] == 0
			&& map[nowY][nowX] > map[newY][newX]){
				visited[newY][newX] = 1;
				dfs(map, newY, newX, visited);
				visited[newY][newX] = 0;
			}
		}
	}

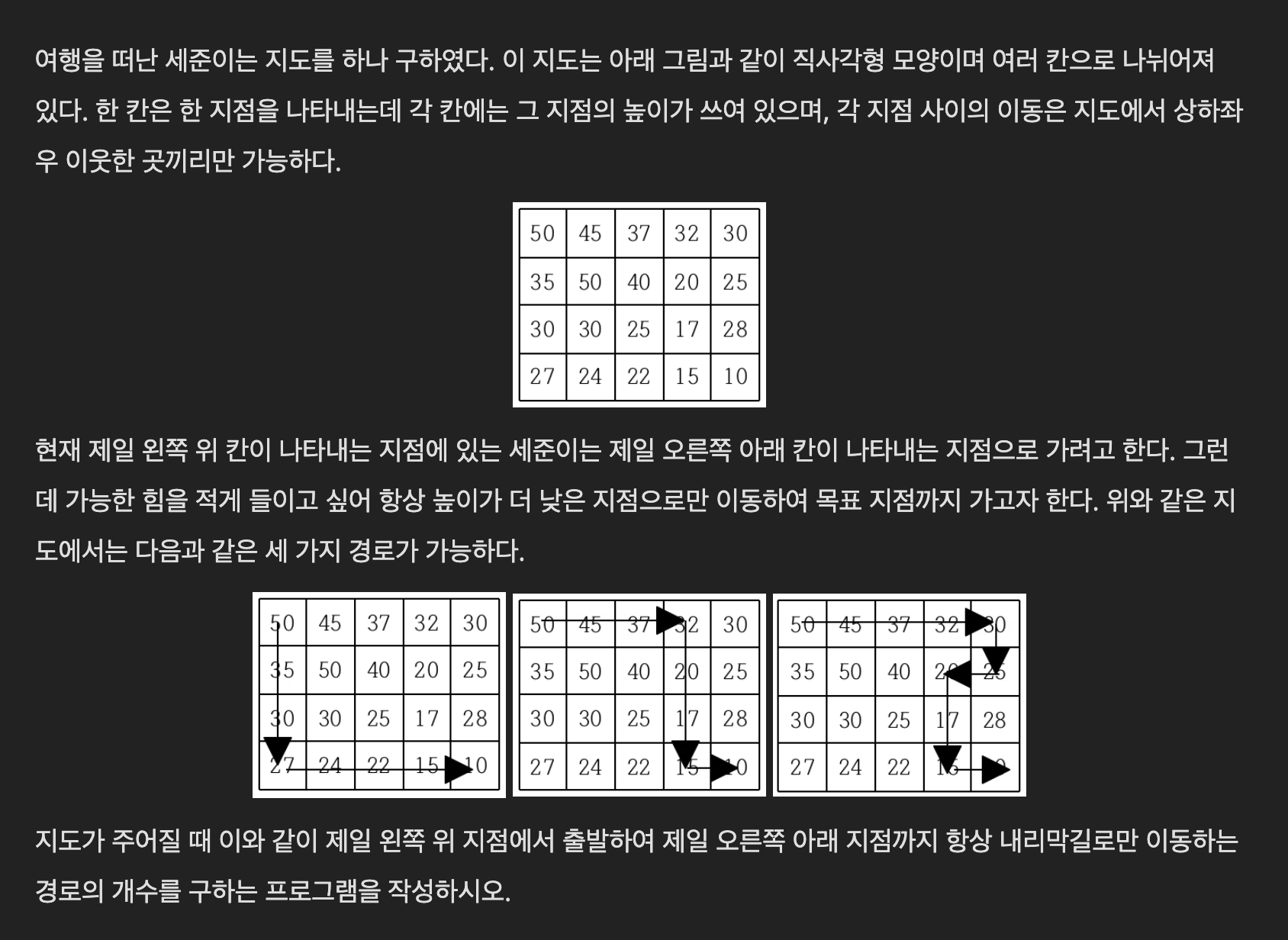
지나온 곳을 다시 탐색하지 않으려고 visited 배열을 이용했다. 그러나 이 방식은 서로 다른 경로에 대해 아무 영향을 미치지 못한다.

visited 배열을 사용하여도 빨간색과 하늘색 경로가 서로 영향을 전혀 주지 않는다.

아이디어

위 그림 예시에서 (3, 1) 좌표 (24)에서 두 개의 경로가 겹치게 된다. 겹치게 되는 순간에 "이 길로 가면 결국 몇 개의 경우의 수로 도착할 수 있어~" 라는 것을 알 수 있어야 한다.

DP 배열을 추가하여 종착지에 도착한 경우 dp배열을 갱신하고 백트래킹할 때 dp의 합을 받아 이미 지나온 길에 대해 다시 한번 탐색하지 않고 이 길로 가면 몇개의 경우의 수로 도착할 수 있는지를 알아내야 한다.

과정

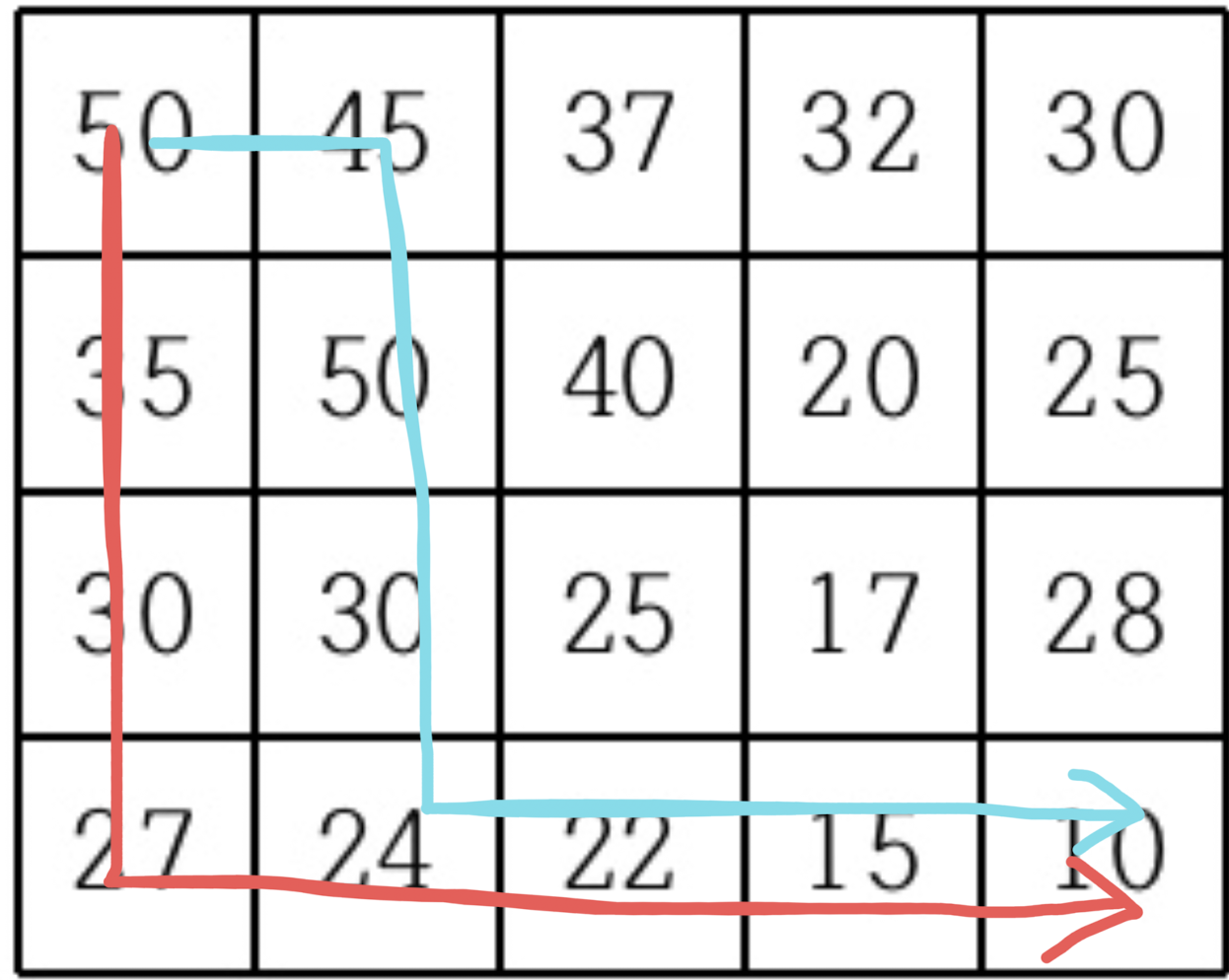
1. 빨간색 선
   DFS 탐색을 통해 목적지 (10)에 도착한다. 이제 백트래킹을 통해 (0, 0)까지 DP를 1로 갱신하며 돌아간다. 이제부터 빨간색 선에 닿는 선들은 더 이상 나아가지 않고 백트래킹을 시작하며 돌아간다. (목적지까지 도착할 수 있는 경우의 수는 1개 뿐이므로)

2. 파란색 선
   탐색하며 빨간색 선에 닿았을 때 백트래킹으로 다시 돌아간다. 이 후 주황색 선으로 분기되는 속에서 다시 탐색한다.

3. 주황색 선
   주황색 선은 탐색하며 파란색 선에 닿았을 때 다시 돌아간다. 분기된 좌표 (0, 3)에서는 파란색과 주황색 dp값이 합쳐져 2가 된다. 또한 원점까지 돌아가며 원점에서는 dp값이 3이 되고 이를 리턴하여 결과값은 3이 된다.

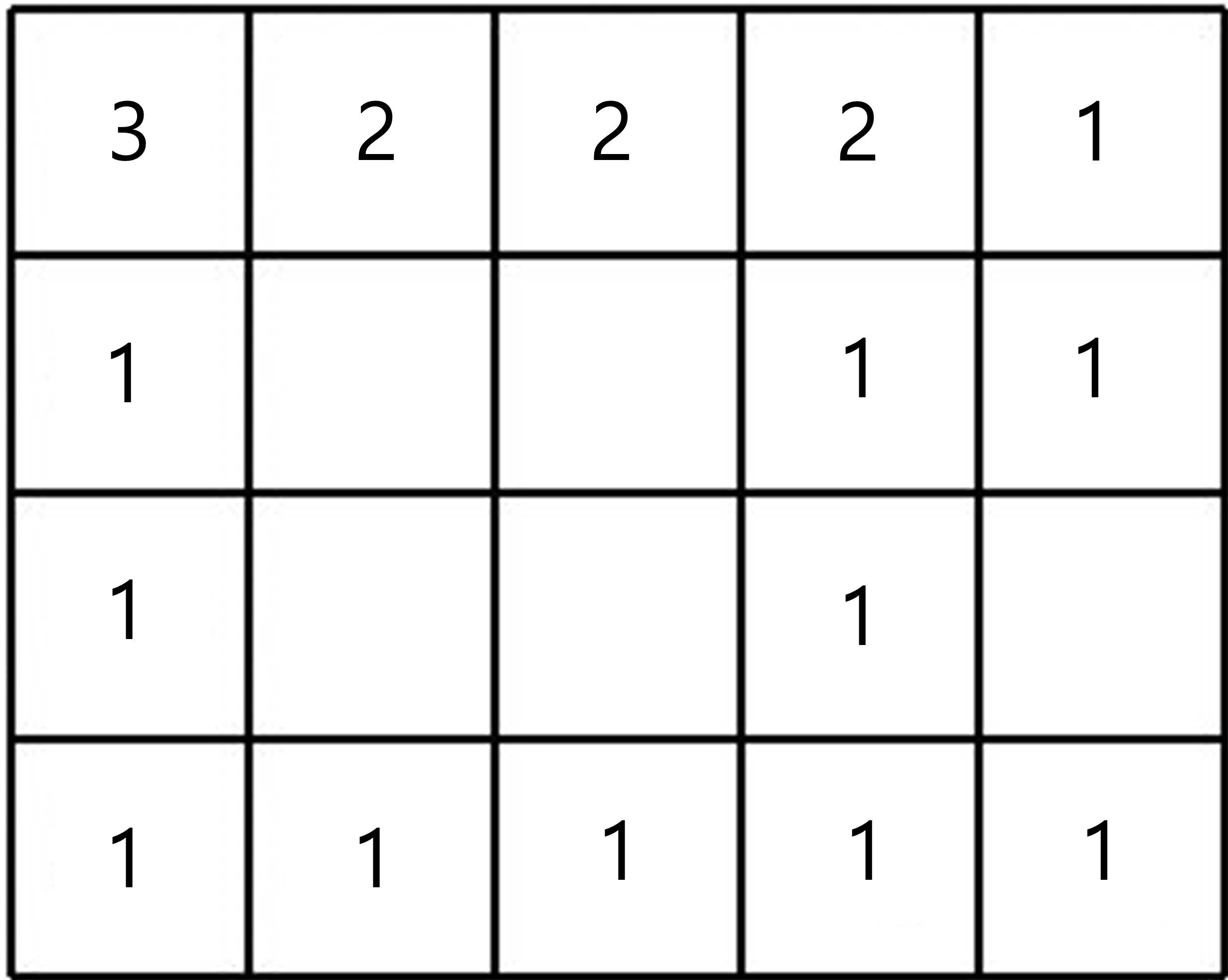
완성된 DP 배열은 다음과 같다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
	static int[] y = {1, -1, 0, 0};
	static int[] x = {0, 0, 1, -1};
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		//StringTokenizer st = new StringTokenizer(br.readLine());

		StringTokenizer st = new StringTokenizer(br.readLine());
		int row = Integer.parseInt(st.nextToken());
		int column = Integer.parseInt(st.nextToken());
		int[][] map = new int[row][column];
		for(int i=0;i<row;i++){
			StringTokenizer st2 = new StringTokenizer(br.readLine());
			for(int j=0;j<column;j++){
				map[i][j] = Integer.parseInt(st2.nextToken());
			}
		}
		int[][] dp = new int[row][column];
		for(int i=0;i<row;i++) Arrays.fill(dp[i], -1);

		System.out.print(dfs(map, 0, 0, dp));
	}
	public static int dfs(int[][] map, int nowY, int nowX, int[][] dp){
		// 도착하면 백
		if(nowY == map.length-1 && nowX == map[0].length-1){
			return 1;
		}
		if(dp[nowY][nowX] != -1){
			return dp[nowY][nowX];
		}

		dp[nowY][nowX] = 0;

		for(int i=0;i<4;i++){
			int newY = nowY + y[i];
			int newX = nowX + x[i];
			if(0 <= newY && newY < map.length
			&& 0 <= newX && newX < map[0].length
			&& map[nowY][nowX] > map[newY][newX]){
				dp[nowY][nowX] += dfs(map, newY, newX, dp);
			}
		}

		return dp[nowY][nowX];
	}
}