부분배열 고르기 (백준, Java)

https://www.acmicpc.net/problem/2104

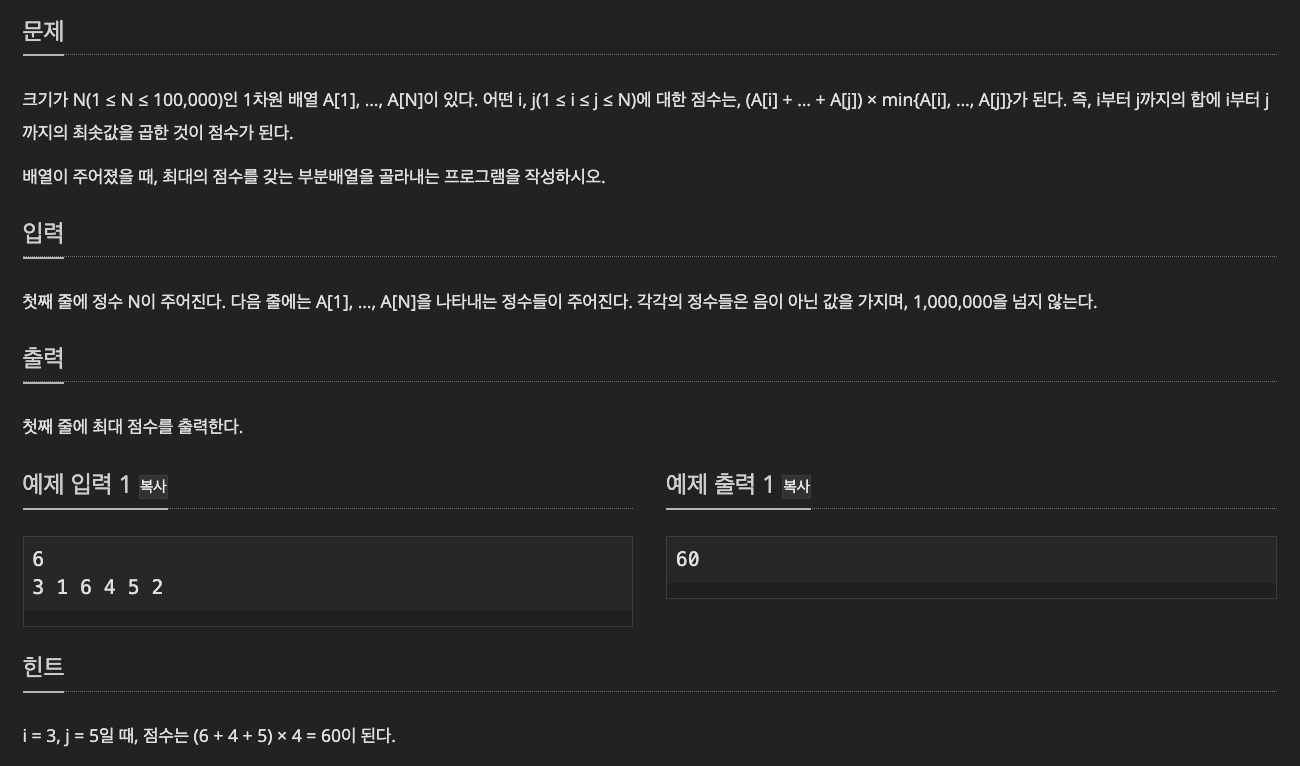
특정 구간의 합 * 특정 구간의 최소값의 최대값을 구해야한다.

💡 기존 아이디어

두 가지의 세그먼트 트리를 만들어서 최댓값을 구하면 된다고 생각했다.

1. 구간의 합을 담은 세그먼트 트리


2. 구간의 최소값을 담은 세그먼트 트리

그 뒤에 2중 반복문으로 가능한 범위를 모두 찾으면 된다고 생각했다.

그러나 문제에서 제시된 길이가 100,000이기 때문에 2중 for문을 사용하면 시간복잡도 O(N^2)로 시간초과가 발생한다.

그렇기에, 분할 정복을 이용해서 적절한 값을 사용해야 한다.

🤔 분할 정복 아이디어

분할 정복을 할 때는 어떤 기준으로 분할 할지를 가장 중요하게 생각해야 한다.

이 문제에서는 어떤 기준으로 기준을 정해야 할까?

이 문제에서는 최소값을 기준으로 분할해야 한다.

예시

문제와 같이 (3, 1, 6, 4, 5, 2) 배열에서 최소값은 2번째 인덱스인 1이다.

1이 포함되었을 때는 최대한 많은 값들을 곱해야 최대값을 얻을 수 있다.

즉 처음 탐색의 범위는 1 ~ 6 전체가 된다.

그 뒤로 다음 범위를 정할 때는 최소값인 1을 기준으로 왼쪽, 오른쪽을 탐색해야 한다.

과정

1번 째 진행 / (3, 1, 6, 4, 5, 2) 전체 확인, 최소값 1

2번 째 진행 / (3) , (6, 4, 5, 2) 확인, 최소값 각각 3, 2

3번 째 진행 / (6, 4, 5) 확인, 최소값 4

4번 째 진행 / (6), (5) 확인, 최소값 각각 6, 5

위 과정에서 도출되는 결과값 중 최대값을 구하는 것이 답이 된다.

시간복잡도

O(N log N)

💻 풀이 코드

import java.io.*;
import java.util.*;

public class Main {
    static int n;
    static int[] arr, minTree;
    static long[] sumTree;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine());

        arr = new int[n + 1];
        arr[0] = Integer.MAX_VALUE; // 최소값 비교를 위해 0번 인덱스 사용
        StringTokenizer st = new StringTokenizer(br.readLine());
        for (int i = 1; i <= n; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }

        sumTree = new long[n * 4];
        minTree = new int[n * 4];

        // 세그먼트 트리 초기화
        buildSumTree(1, 1, n);
        buildMinTree(1, 1, n);

        // 최대 점수 계산 및 출력
        System.out.println(findMaxScore(1, n));
    }

    // 분할 정복
    private static long findMaxScore(int start, int end){
        // 탐색 범위를 벗어나면 최댓값을 구해야하므로 return 0
        if(start > end) return 0;

        // 현재 범위의 최소값 인덱스
        int minIndex = queryMin(1, 1, n, start, end);
        // 현재 범위의 합
        long sumNum = querySum(1, 1, n, start, end);
        // 직사각형의 넓이
        long area = arr[minIndex] * sumNum;

        // 반으로 쪼갤 수 있으면 왼쪽 탐색
        if(start < minIndex){
            area = Math.max(area, findMaxScore(start, minIndex - 1));
        }
        // 반으로 쪼갤 수 있으면 오른 쪽 탐색
        if(minIndex < end){
            area = Math.max(area, findMaxScore(minIndex + 1, end));
        }

        // 최대 넓이 리턴
        return area;
    }

    // 특정 범위 최소값 찾기
    private static int queryMin(int node, int start, int end, int left, int right){
        if(start > right || end < left) return -1;
        if(left <= start && end <= right) return minTree[node];

        int mid = (start + end) / 2;
        int leftMin = queryMin(node * 2, start, mid, left, right);
        int rightMin = queryMin(node * 2 + 1, mid + 1, end, left, right);

        return getMinIndex(leftMin, rightMin);
    }

    // 특정 범위 합 찾기
    private static long querySum(int node, int start, int end, int left, int right){
        if(start > right || end < left) return 0;
        if(left <= start && end <= right) return sumTree[node];

        int mid = (start + end) / 2;
        return querySum(node * 2, start, mid, left, right)
                + querySum(node * 2 + 1, mid + 1, end, left, right);
    }

    // 합 트리 구축
    private static long buildSumTree(int node, int start, int end){
        if(start == end){
            return sumTree[node] = arr[start];
        }
        int mid = (start + end) / 2;
        return sumTree[node] = buildSumTree(node * 2, start, mid)
                + buildSumTree(node * 2 + 1, mid + 1, end);
    }

    // 최소값 트리 구축
    private static int buildMinTree(int node, int start, int end){
        if(start == end) return minTree[node] = start; 

        int mid = (start + end) / 2;
        int leftMin = buildMinTree(node * 2, start, mid);
        int rightMin = buildMinTree(node * 2 + 1, mid + 1, end);
        return minTree[node] = getMinIndex(leftMin, rightMin);
    }

    // 더 작은 인덱스 확인 함수
    private static int getMinIndex(int leftMin, int rightMin){
        if(leftMin == -1) return rightMin; 
        if(rightMin == -1) return leftMin;

        if(arr[leftMin] < arr[rightMin]) return leftMin;
        else if(arr[leftMin] > arr[rightMin]) return rightMin;
        else return Math.min(leftMin, rightMin);
    }
}