서로 다른 자연수의 합 (백준, Java)

https://www.acmicpc.net/problem/9764

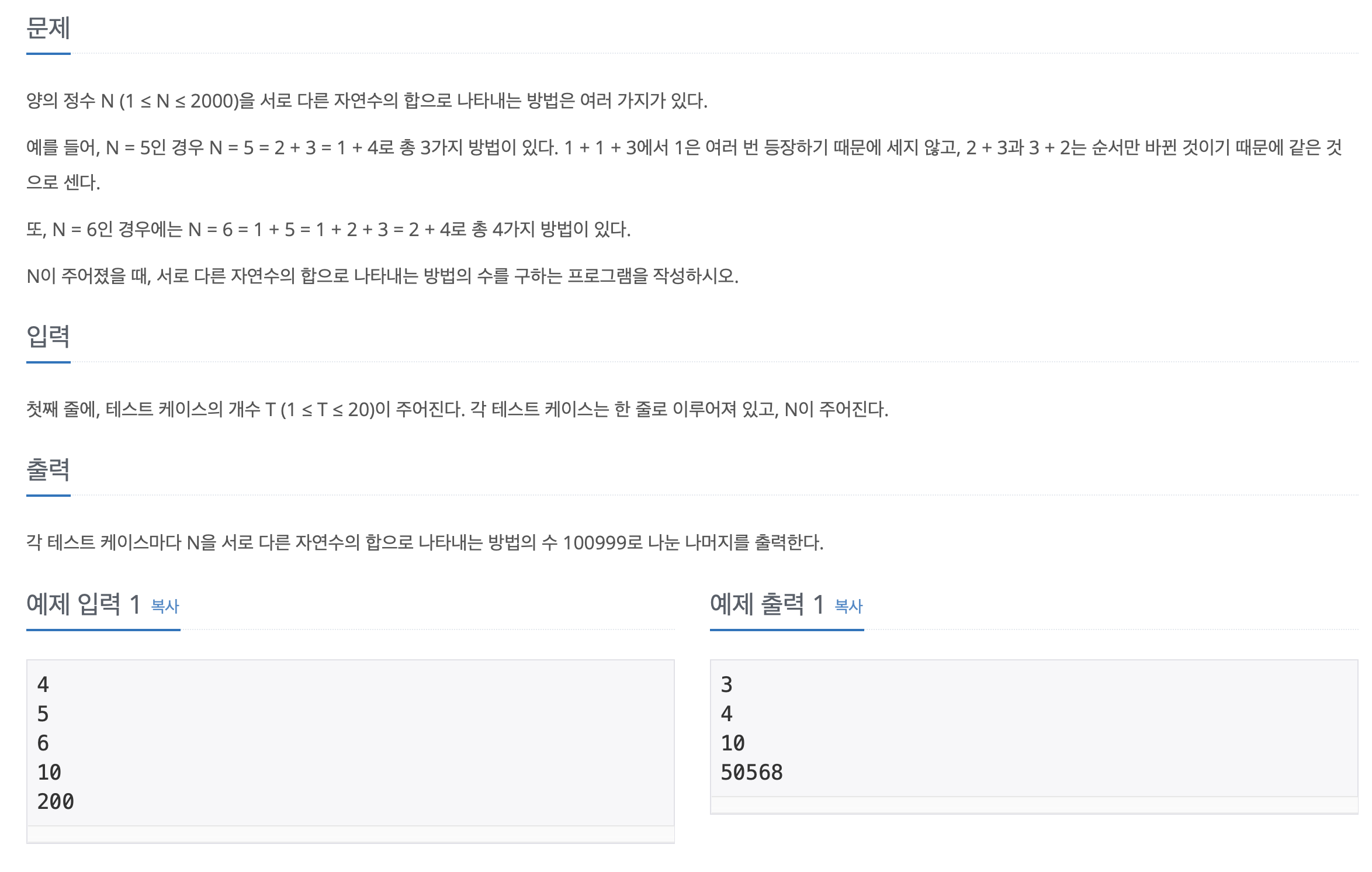
틀린 아이디어

DP 문제라는 것은 쉽게 알 수 있다. 그러나, 중요한 조건이 존재한다.

서로 다른 자연수
즉, 중복되지 않는 조합의 수를 세어야 한다.

만약, 서로 다른 자연수라는 조건이 없다면 DP 점화식 코드는 다음과 같이 작성된다.

for (int i = 1; i <= N; i++) {      
    for (int j = i; j <= N; j++) {  
        dp[j] += dp[j - i];
    }
}

이 코드는 특정 수를 자연수의 합으로 표현해야할 때 올바른 코드가 되지만, 문제의 서로 다른 자연수의 합으로만 구성되어야 한다는 조건을 달성할 수 없다.

잘못된 이유

현재 사용하는 숫자가 3인 경우에 코드에서는 다음과 같이 작동한다

dp[3] += dp[0];
dp[4] += dp[1];
dp[5] += dp[2];
dp[6] += dp[3]; <<< 사고발생!!!!!

dp[3] += dp[0];는 3을 사용하여 3을 만드는 경우를 뜻한다. 즉, 3으로 3을 만드는 경우이므로 1이다.

하지만 이후 dp[6] += dp[3];에서 해당 3을 이용하게 되는데, 이는 3을 이용하여 6을 만드는 경우이다.

이 경우에 6을 만드는 경우의 수로 "3 + 3"을 포함하게 되는 것이다

이는 서로 다른 자연수의 합을 이용해야 한다는 조건을 위반한다.

맞는 아이디어

안쪽의 for문이 큰 수부터 확인하도록 해야한다.

for (int i = 1; i <= N; i++) {    
    for (int j = N; j >= i; j--) {   
        dp[j] = dp[j] + dp[j - i];
    }
}

N부터 거꾸로 내려오게 되면 현재 값을 계산할 때 필요한 이전 값 (j-i)에 i를 더하지 않은 순수 값만을 참조할 수 있게 된다.

예시

틀린 예시와 비슷한 상황이다.

dp[6] += dp[3]; <<< 이곳에서 참조하는 dp[3]은 아직 "3" 자체의 경우를 포함하지 않는다!
dp[5] += dp[2];
dp[4] += dp[1];
dp[3] += dp[0]; <<< 이곳에서 "3" 자체의 경우를 더하게 된다

코드

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        //StringTokenizer st = new StringTokenizer(br.readLine());

        int[] dp = new int[2001];
        dp[0] = 1;
        for(int i=1;i<=2000;i++){
            for(int j=2000;j>=i;j--){
                dp[j] += dp[j-i];
                dp[j] %= 100999;
            }
        }

        int input = Integer.parseInt(br.readLine());
        for(int i=0;i<input;i++){
            int temp = Integer.parseInt(br.readLine());
            System.out.println(dp[temp]);
        }
    }
}